Усилие гибки можно определить как аналитически, так и по экспериментальным формулам. Аналитически усилие гибки определяется исходя из равенства внешнего изгибающего момента моменту внутренних сил. Рассмотрим гибку V – образной детали (рис.11.5). Изгибающий момент для любой стадии гибки определяется как:

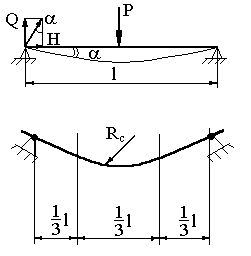
Рис. 11.5 Схема к определению усилия гибки V-образной детали.

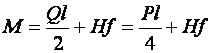
Где расстояние между опорами, а стрела прогиба.

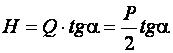
Максимальное усилие, как это установлено опытами, имеет место при . Отвечающая этому усилию стрела прогиба будет:

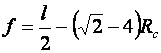
Изгибающий момент

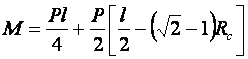
Но 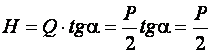при и усилие

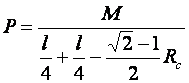или 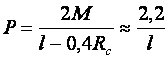(11.18)

Изгибающий момент (по Марковцу) равен:

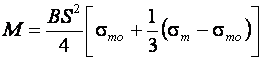
Экстраполированный предел текучести определяется по диаграмме истинных напряжений как

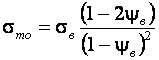
А истинное напряжение, отвечающее данной степени деформации

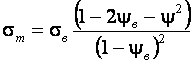
Подставляя значения и в уравнение момента имеем:

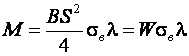
Так как

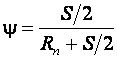
То

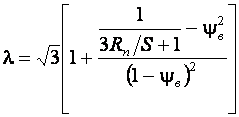или

Окончательно

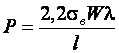(11.19)

Усилие гибки П-образных штампах можно определить следующим образом. Принимая за плечо гибки в конечный момент запишем изгибающий момент:

,

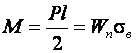А отсюда усилие будет:

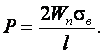
Учитывая трение (около 30% от усилия гибки) получим:

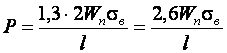
Или окончательно:

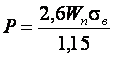(11.20)

В литературе рекомендуется ряд формул для определения усилия гибки:

1) для гибки V-образных деталей –

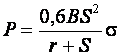(11.21)

2) для гибки П-образных деталей –

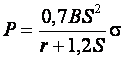(11.22)

Где радиус гиба (радиус пуансона), напряжение в крайних волокнах принимаемое .

3) для свободной одноугловой гибки

4)

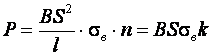(11.23)

Где расстояние между опорами, коэффициент, учитывающий упрочнение коэффициент. Зависящий от отношения и равный 0,23 – 0,06 (при ).

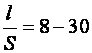5) для гибки П-образных деталей с прижимом:

(11.24)

6) для гибки V-образных деталей с калибровкой

Где площадь заготовки пол пуансоном при калибровке, удельное давление равное 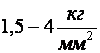для алюминия, 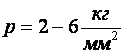для латуни, 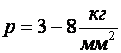для стали 10 – 20 и 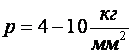для стали .

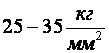7) для свободной гибки без подчеканки

(11.25)

Где коэффициент запаса, коэффициент = 0,06 -0,55 (в зависимости от схемы гибки). Характер индикаторных кривых усилий для различных случаев гибки показан на рис 11.6.

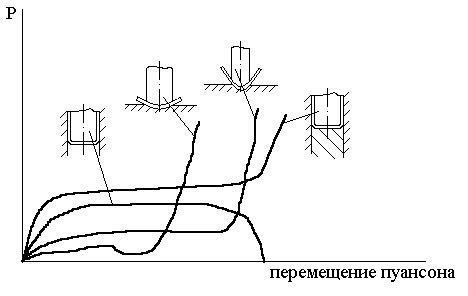
Рис.11.6 Характер индикаторных кривых усилия
гибки при различных процессах гибки.