Упрочнение материала и его сопротивление при гибке. Влияние упрочнения на величину напряжений при гибке . и момент сопротивления
 21 июня, 2013
21 июня, 2013  admin
admin Распределение напряжений ![]() и
и ![]() с учетом упрочнения может быть найдено совместным решением уравнения (9.3) и уравнения пластичности (9.4). Однако, в последние два уравнения вместо подставляют истинное напряжение, определяемое по кривым упрочнения, в зависимости от величины деформаций. Используем линейную зависимость истинного напряжения от относительного уменьшения площади поперечного сечения
с учетом упрочнения может быть найдено совместным решением уравнения (9.3) и уравнения пластичности (9.4). Однако, в последние два уравнения вместо подставляют истинное напряжение, определяемое по кривым упрочнения, в зависимости от величины деформаций. Используем линейную зависимость истинного напряжения от относительного уменьшения площади поперечного сечения ![]() , т. е.
, т. е. ![]() . Причем при учете упрочнения воспользуемся кривой истинных напряжений 2-го вида. Воспользуемся также эквивалентностью деформаций. Эквивалентными деформациями называются такие, которые изменяются в одинаковых пределах и равноценны по упрочняющему эффекту. Например, относительное сужение поперечного сечения при растяжении эквивалентно относительному укорочению при сжатии. Значение эквивалентных деформаций при изгибе (пренебрегая изменением ширины заготовки) определяем для зоны сжатия:
. Причем при учете упрочнения воспользуемся кривой истинных напряжений 2-го вида. Воспользуемся также эквивалентностью деформаций. Эквивалентными деформациями называются такие, которые изменяются в одинаковых пределах и равноценны по упрочняющему эффекту. Например, относительное сужение поперечного сечения при растяжении эквивалентно относительному укорочению при сжатии. Значение эквивалентных деформаций при изгибе (пренебрегая изменением ширины заготовки) определяем для зоны сжатия:
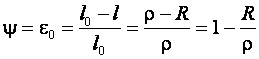 (10.1)
(10.1)
Для растянутых:
![]() (10.2)
(10.2)
Известно, что линейная зависимость между истинным напряжением и относительным сужением по диаграммам 2-го вида определяется уравнением касательной
![]()
![]() (10.3)
(10.3)
Где ![]() истинное напряжение,
истинное напряжение, ![]() экстраполированный предел текучести,
экстраполированный предел текучести, ![]() модуль упрочнения,
модуль упрочнения, ![]() степень деформации.
степень деформации.
Используя уравнения (10.1), (10.2) и (10.3), можно записать для зоны сжатия:
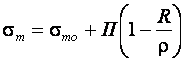 (10.4)
(10.4)
И растяжения
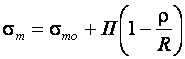 (10.5)
(10.5)
Решая совместно уравнения (9.3), уравнение пластичности (9.4) и (10.4) для зоны сжатия, получим:
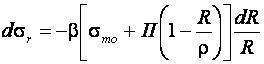 (10.6)
(10.6)
Интегрируя в пределах от ![]() до
до ![]() и определив значение постоянной интегрирования для граничных условий
и определив значение постоянной интегрирования для граничных условий ![]() и
и ![]() получим
получим
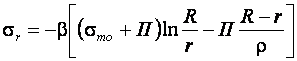 (10.7)
(10.7)
И
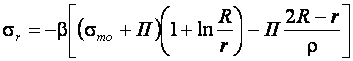 (10.8)
(10.8)
Для зоны растяжения
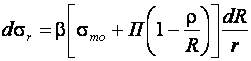 (10.9)
(10.9)
Интегрируя от ![]() до
до ![]() и находя
и находя ![]() из условия
из условия ![]() и
и ![]() , получим:
, получим:
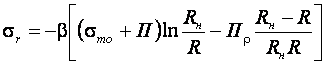 (10.11)
(10.11)
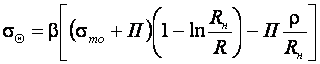 (10.12)
(10.12)
10.2. Изгибающий момент при гибке.
Величина внешнего изгибающего момента, потребного для осуществления пластического изгиба, может быть определена из условия равенства внешних моментов сил, моментам внутренних сил, т. е.
![]() (10.10)
(10.10)
Момент внутренних сил определяется как сумма моментов, создаваемых напряжениями ![]() и определяемых в общем случае интегралом вида
и определяемых в общем случае интегралом вида ![]() для участков по толщине заготовки, в которых
для участков по толщине заготовки, в которых ![]() не меняется, т. е.
не меняется, т. е.
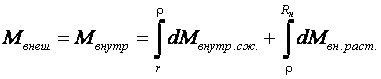 (10.11)
(10.11)
Полагая, что нейтральный слой при гибке делит толщину заготовки пополам, т. е. 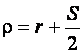 и деформация идет без упрочнения, получим:
и деформация идет без упрочнения, получим:
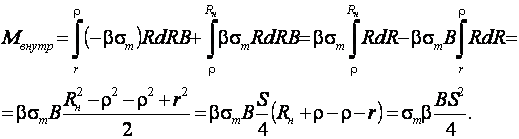 (10.12)
(10.12)
Момент сопротивления при пластическом изгибе
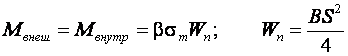 (10.13)
(10.13)
А при упругой деформации
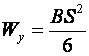 (10.14)
(10.14)
Поэтому
![]() (10.15)
(10.15)
И с учетом утонения
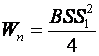
В общем случае момент сопротивления зависит от формы поперечного сечения заготовки, так что можно сказать, что при изгибе 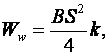 где
где ![]() коэффициент, учитывающий форму поперечного сечения заготовки.
коэффициент, учитывающий форму поперечного сечения заготовки. ![]() для прямоугольного сечения;
для прямоугольного сечения; ![]() для круглого;
для круглого; ![]() двутаврового.
двутаврового.
При изгибе без упрочнения по относительно маленькому радиусу величина изгибающего момента внутренних сил определяется аналогично, но вместо ![]() надо поставить величину
надо поставить величину ![]() .
.
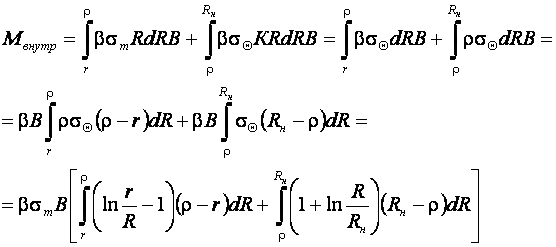
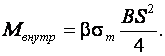
Аналогично можно определить момент внутренних сил и при учете упрочнения. Однако это сложные вычисления. В целях их упрощения будем считать, что напряжения в крайнем волокне определяется по кривой истинных напряжений 2-го вида или по касательной к этой кривой, пренебрегая смещением нейтрального слоя, т. е. наличием радиальных напряжений. По Марковицу, эпюра распределения напряжений для сжатой зоны будет (в растянутой зоне тоже, но с обратным знаком). По Марковицу, напряжение на нейтральном слое ![]() ,
, ![]() истинное напряжение производимое деформацией.
истинное напряжение производимое деформацией.
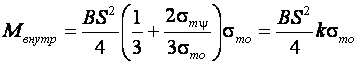 (10.16)
(10.16)
Где ![]() коэффициент, учитывающий упрочнение. Упрочнения не будет при
коэффициент, учитывающий упрочнение. Упрочнения не будет при ![]()

 Опубликовано в
Опубликовано в