The van Roosbroeck-Shockley model
 4 марта, 2014
4 марта, 2014  admin
admin The van Roosbroeck-Shockley model allows one to calculate the spontaneous radiative recombination rate under equilibrium and non-equilibrium conditions. To calculate the recombination rate, the model requires the knowledge of only a few basic parameters, namely the
bandgap energy, the absorption coefficient, and the refractive index. All of these parameters can be determined by simple, well-known experimental methods.
Consider a semiconductor with an absorption coefficient a(v) given in units of cm-1. A photon is generated in the semiconductor by electron-hole recombination and is subsequently absorbed, as illustrated in Fig. 3.1. The mean distance a photon of frequency v travels before being absorbed is simply a(v)-1. The time it takes for a photon to be absorbed is given by
|
t(v) = |
|
(3.12) |
1
a(v) vgr
where vgr is the group velocity of photons propagating in the semiconductor. The group velocity of photons is given by
|
dro dk |
|
dv |
|
(3.13) |
|
Kgr |
|
d(1/ X) |
|
d(n v) |
|
= c ■ |
|
dv |
where n is the refractive index. Inserting the group velocity into Eq. (3.12) yields
|
(3.14) |
—1— = a(v) v gr = a(v) c —dv—
t(v) gr d(n v)
This equation gives the inverse photon lifetime or photon absorption probability per unit time. The product of the absorption probability and the photon density yields the photon absorption rate per unit time per unit volume.
|
|
Under equilibrium conditions, the density of photons per unit volume in a medium with refractive index n is given by Planck’s black-body radiation formula
|
8 n ~Xr |
|
1 |
|
N (X)dX = |
|
dX |
|
(3.15) |
|
hv/kT і e1 |
from which we can readily obtain N(v) dv, the number of photons having frequencies in the interval v and v + dv. We have X = c / (n v), so that
|
(3.16) |
dX = V dv.
(n v)2 dv
|
|
Inserting this value in Eq. (3.15) yields Planck’s black-body photon distribution as a function of frequency
(3.17)
The absorption rate per unit volume in the frequency interval v and v + dv is given by the photon density divided by the mean lifetime of photons
|
2 2 ______ 8nv n d(n v) |
|
N (v) T(v) |
|
1 |
|
Rq(v) = |
|
(3.18) |
|
dv ehv / kT -1 |
|
3 |
|
c |
|
dv a(v)c ---------------- d(n v) |
Integration over all frequencies yields the absorption rate per unit volume
|
a(v) |
|
dv |
|
(3.19) |
|
0 |
|
hv/kT і e -1 |
|
2 |
|
R0 = J * R0(v)dv = J |
|
* 8nv2 n2 |
|
c |
which is the celebrated van Roosbroeck-Shockley equation. The van Roosbroeck-Shockley equation can be simplified by writing the absorption coefficient as
a = a0 ^ (E - Eg)/ Eg. (3.20)
The square-root dependence of the absorption coefficient is motivated by the proportionality of the absorption coefficient and the density of states, which in turn follows a square-root dependence on energy. Note that a0 is the absorption coefficient at hv = 2Eg. Approximate values of a0 for several semiconductors are given in Table 3.1.
The van Roosbroeck-Shockley equation can be simplified further by neglecting the frequency dependence of the refractive index and using the refractive index value at the band edge. One obtains
(3.21)
|
|
where x = hv/(kT) = E/(kT) and xg = Eg /(kT). Owing to the strong increase of the exponential function with x, only a small range of energies close to the bandgap contributes to the integral. The integral has no simple analytical solution and it needs to be evaluated by a numerical method.
|
Table 3.1. Bimolecular recombination coefficient at 300 K for different semiconductors as calculated from the energy gap, absorption coefficient, and refractive index at the bandgap energy. The spontaneous lifetime is given by B 1 ND, A-1 and it is calculated for a majority carrier concentration of 1018 cm-3.
|
Under equilibrium conditions, the carrier generation rate (photon absorption rate) is equal to the carrier recombination rate (photon emission rate). Thus, the van Roosbroeck-Shockley model provides the equilibrium recombination rate. As discussed earlier, the bimolecular rate equation, which applies to both equilibrium and non-equilibrium conditions, gives the number of recombination events occurring per unit volume per unit time:
|
(3.22) |
R = Bn p
|
|
Next, we use the van Roosbroeck-Shockley model to calculate the bimolecular recombination coefficient B. Under equilibrium conditions, it is R = R0 = Bni2. Thus the bimolecular recombination coefficient is related to the equilibrium recombination rate by
(3.23)
Table 3.1 shows the bimolecular recombination coefficient for different semiconductors as calculated from Eqs. (3.21) and (3.23). All material parameters used in the calculation are given in the table. The calculated results reveal that B = 10-9-10-11 cm3/s for direct-gap III-V semiconductors. This calculated result agrees well with experimental results. GaP, Si, and Ge, all indirect-gap semiconductors, have a much smaller bimolecular recombination coefficient compared with direct-gap III-V semiconductors.
There are several other ways to calculate the bimolecular recombination coefficient. An early calculation by Hall (1960) using a two-band model produced a bimolecular recombination coefficient of
|
2 |
|
3 ( |
|
me + me I * * mh me) |
|
3/2 ( E Л |
|
300 K T |
|
(3.24) |
|
B = 5.8 x 10 |
|
n |
|
V 1eV ) |
|
mh+me |
|
|
e m e s |
|
-13 cm |
|
s |
|
л |
|
-3/2 |
where me*, mh*, and me are the effective electron mass, effective hole mass, and free electron mass, respectively. Garbuzov (1982) described a simple quantum mechanical calculation for direct-gap semiconductors and obtained the following expression for the bimolecular recombination coefficient:
|
2 |
|
3/2 |
|
3 |
|
Eg |
|
-10 cm |
|
300 K T |
|
(3.25) |
|
V 15eV ) |
|
s |
|
B = 3.0 x 10 |
|
coefficient is in the 10 10 cm3/s range when calculated for GaAs at 300 K using Eqs. (3.21) and |
All of the methods described here to calculate B give reasonably similar results. The B coefficient is in
(3.23) - (3.25).


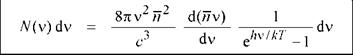
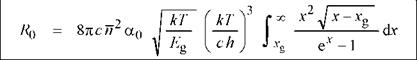
 Опубликовано в
Опубликовано в