The first theory of optical transitions was developed by Albert Einstein. The Einstein model includes spontaneous and stimulated or induced transitions. Spontaneous transitions occur spontaneously, that is, without an external stimulus. In contrast, stimulated transitions are induced by an external stimulus, namely a photon. Thus the induced transition rates are proportional to the photon density or radiation density.

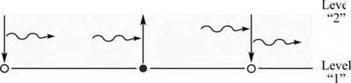
The coefficients A and B describe spontaneous and stimulated transitions in an atom with two quantized levels. These transitions are illustrated schematically in Fig. 3.5. Denoting the two levels as “1” and “2”, Einstein postulated the probability per unit time for the downward transition (2 ^ 1) and upward transition (1 ^ 2) as

W2^-1 - B 2^-1 p(v) + A

and

The downward transition probability (per atom) has two terms, namely the induced term and the spontaneous term. The induced term, B 2^1 p(v), is proportional to the radiation density p(v). The spontaneous downward transition probability is a constant A- Note that the spontaneous lifetime is given by ispont = A 1 . The upward probability is just B 1^2 p(v).

Fig. 3.5. Spontaneous emission, in­duced absorption, and induced emis­sion events in the two-level atom model. Initially occupied and unoc­cupied levels are indicated by solid and open circles, respectively.

The Einstein A coefficient in an atom corresponds to the bimolecular recombination coefficient in a semiconductor. In an atom, the concentration terms (i. e. n and p in the bimolecular rate equation R = Bn p) do not come into play, since for a downward transition to occur, the upper level must be occupied (one electron, “n = 1”) and the lower level must be unoccupied (one hole, “p = 1”).

Einstein showed that B = B 2^1 = B 1^2. Thus stimulated absorption and stimulated emission are complementary processes. He also showed that the ratio of the coefficients at a frequency v in an isotropic and homogeneous medium with refractive index n is a constant given by A/B = 8n n 3 h v3 / c3.

The equivalence of B2^1 and B 1^2 can also be shown by quantum mechanical considerations, namely by using Fermi’s Golden Rule. However, a detailed discussion of the Einstein model goes beyond the scope of this discussion.