§4.1. Основные допущения, принимаемые в инженерных методах
определения сварочных деформаций и напряжений

Процесс образования сварочных деформаций и напряжений характеризуется упругопластичеоким поведением металла, не - стационарна®! температурными условиями, высоким уровнем тем­пературы при резко неравномерном ее распределении. В ряде случаев еще не представляется возможным достаточно полно от­разить термомеханические процессы, происходящие в металле при сварке. Поэтому возникает необходимость разработки при­ближенных расчетных методов определения сварочных деформаций и напряжений. Эти методы должны быть прости и обеспечивать в то же время необходимую для практических целей точность. Удовлетворить одновременно требованиям простоты и точности можно путем выбора эффективных расчетных схем, которые

должны учитывать только основные, определяющие факторы и пренебрегать второстепенными особенностями процесса. Именно в этом направлении развиваются инженерные методы теории сва­рочных деформаций и напряжений. Образование временных и остаточных деформаций и напряжений при сварке связано с объ­емными изменениями металла. По мере распространения теплоты и выравнивания температуры происходит непрерывное изменение и перераспределение объема металла. Изменение объема металла

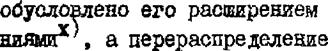при нагреве и фазовыми превраще-

объема металла является резудь - татом пластических деформаций и охватывает область, приле­гающую к шву. Пластические деформации в продельном и попе­речном по отношению к оси шва направлениях зависят главная образом от тепловых характеристик процесса сварки и свойств металла и в значительно меньшей степени от характеристик же­сткости свариваемых элементов. Поэтому перераспределение объема металла в районе сварных соединений практически оди­наково как в сложных конструкциях, так и в простейших эле­ментах. Это обстоятельство позволяет задачу определения

х) Фазовые превращения, происходящие при высоких температу­рах, когда металл находится в состоянии полного разупроч­нения, практически не отражаются на процессе образования

сварочных деформаций и напряжений расчленить на две части, Б первой из них определяют остаточные пластические деформа­ции, обусловливающие перераспределение объема металла в районе сварного соединения (термомеханическая задача), Во второй части определяют деформации конструкции в целом, вследствие перераспределения объема металла в районе сварных соединений (деформационная задача).

Определение остаточных пластических деформаций в районе сварных соединений выполняется на базе рассмотрения термоме - хагшческйх процессов, вызываемых сварочным нагревом. Эта часть задачи веема специфична. Рассмотрение ее для различ­ных условий сварки - основное содержание теории сварочных деформаций и напряжений. Вторая часть задачи не является спе­цифической. Аналогичные задачи рассматриваются в теории остаточных напряжений, вызываемых другими технологическими процессами, а также в теории температурных напряжений. Реше­ние их гложет быть выполнено методами сопротивления материа­лов прикладной теории упругости. Расчленение задачи о сва­рочных дефошлациях и напряжениях на указанные две части яв­ляется одной из основных идей ее приближенного решения. Дело э том, что при решении термомеханической задачи основное зна­чение имеет характер распределения температуры, деформаций и напряжений в относительно узкой области, расположенной за источником теплоты и прилегающей к оси его перемещения. Опи­сание процесса распространения теплоты в этой области может быть существенно упрощено принятием схем мощных быстродви­

жущихся источников теплоты, а распределение деформаций и на­пряжений - принятием допущения об одномерности напряженного состояния. Важно еще раз отметить, что решение термомехани­ческих задач получают на простейших элементах, сосредоточи­вая свое внимание на указанной вше области и используя условия подобия процесса развития пластических деформаций.

При решении термомеханической задачи удается также уп­ростить изучение истории процесса образования деформаций и напряжений. Как показано в § 2.2, для определения напряжений в данный момент упругопластического деформирования элемента достаточно знать его паяную деформацию, если он испытывает нагружение, а если идет процесс разгрузки, то, кроме того, необходимо знать деформацию элемента в момент начала раз­грузки. Для области, прилегающей к оси шва и подвергаемой

высокому нагреву, это положение означает, что до момента мак­симального нагрева идет процесс нагрузки, а с момента охлаж­дения начинается процесс разгрузки. Следовательно, для оцен­ки остаточных пластических деформаций изучение истории про­цесса можно ограничить рассмотрением упругодластического деформирования того или иного элемента в момент его макси­мального нагрева и после полного остывания.

Остаточные пластические деформации при сварке, как от­мечалось, зависят главным образом от свойств металла и теп­ловых характеристик процесса. Что касается свойств металла, то возможная их идеализация обсуждалась в § 2.1j тепловые же характеристики процесса зависят от мощности источника тепла, толщины свариваемых элементов, теплоотдачи с поверхности. Кро­ме того, на процесс образования пластических деформаций ока­зывают влияние характеристиш жесткости элемента и наличие в нем начальных напряжений. Таким образом, на величину к ха­рактер распределения пластических деформаций оказывает влия­ние целый ряд факторов. Одновременный учет их вызывает опре­деленные затруднения, вместе с тем расчеты указывают на их незначительное взаимное влияние. Поэтому в инженерных мето­дах делается допущение о малом взаимном влиянии указанных факторов на остаточные пластические деформации. Это допуще­ние дает возможность рассматривать влияние того или иного фактора изолированно от других, а лишь затем оценивать их суммарное действие. Основное достоинство такого подхода простота и наглядность решения, позволяющего довести до ана­литического выражения искомые зависимости.

Кратко резшшруем сделанные замечания об основных упро­щениях и допущениях, принимаемых в инженерных методах опре­деления сварочных деформаций и напряжений:

1. Задача в целом расчленяется на две части - термоме- хашческув и деформационную.

2. Цель термомеханической задачи - оценить перераспре­деление объема металла в районе сварного соединения вслед­ствие пластических деформаций металла.

3. Цель деформационной задачи - определение перемещений, деформаций и напряжений конструкции в целом, возникающих в результате перераспределения объемов металла в районах сварных соединений.

4. Решение термомеханических задач выполняется на про- стейшкх элементах при следующих допущениях:

а' предполагается одномерность напряженного состояния я используется гипотеза плоских сечений;

б) упрощается изучение истории процесса деформирования, а именно предполагается, что процесс нагрева сопровождает­ся нагрузкой, а охлаждения - разгрузкой металла (с возможной поел едущей нагрузкой противоположного знака);

в) принимается диаграмма растяжения-сжатия для идеаль­ного упругопластического материала и упрощенная зависимость механических свойств от температури;

г) используются схемы модных быстродвижущихся источни­ков теплоты;

д) влияние ряда факторов (теплоотдача, толщина, конеч­ная жесткость, начальное напряженное состояние) рассматри­вается изолированно, т. е. делается допущение об их малом взаимном влиянии.

Отметим, что принципиальным является допущение об одно­мерности напряженного состояния. Что касается остальных до­пущений, то они не являются обязательными и можно, оставаясь в рамках инженерных методов, получить решения без тех или иных перечисленных допущений, что приводит, естественно, к усложнению аналитических решений или к необходимости исполь­зования численных методов. В частности, допущение 4в, спра­ведливое дяя низкоуглеродистых и низколегированных^ сталей, оказывается неприемлемым при рассмотрении деформаций и на­пряжений при сварке некоторых сплавов и закаливающихся ста­лей. Поэтому анализ термомеханических процессов при сварке этих сталей и сплавов выполняется в § 4.7 без допущения 4в.

В отношении основного допущения об одномерности напря­женного состояния в высокотемпературной области, расположен­ной позади источника, необходимо сделать следующие замеча­ния.

При сварке листовых конструкций на некотором удалении от источника теплоты изотермические поверхности вытягиваются к градиенты температур вдоль оси шва становятся значительно меньше, чем поперек. Поэтому, если исключить из рассмотрения область впереди источника теплоты, которая не оказывает за­метного влияния на дальнейший процесс образования деформа­ций и напряжений, то можно пренебречь изменениями температу­ры вдоль оси шва. Это в свою очередь позволяет считать зада-

чу одномерной к пренебречь напряжениями хх^ и по срав­нению с напряжениями 6^ , действующими по кадравленею осе шва. Допущение об одномерном характере напряженного состоя­ния в указанной. области оправдывается также наличием зоны, нагретой вше Тх, в пределах которой напряжения отсутству­ют. Эта зона, ограниченная изотермой Т* , вытянута вдоль оси шва и разделяет пластину в районе высокого нагрева на две части, между которыми нет силового взаимодействия.

Погрешности от принятия допущения одномерности - напря­женного состояния тем меньше, чем вше скорость сварки и ни­же коэффициент температуропроводности металла, т. е. чем в большей степени вытягиваются изотермические поверхности. Если. предположить одновременность наложения шва по всей длине пла­стины (или его выполнение СО скоростью 1Гс;*-о«) и пренебречь концевыми эффектами, охватывающими относительно небольшие области у концов шва (порядка ширины пластической зоны), то допущение об одномерности напряженного состояли оправдывает­ся полностью.

Некоторые дополнительные соображения о справедливости сделанных допущений при одних условиях сварки я ограниченной пригодности при других будут приведены при рассмотрении кон­кретных примеров сварки простейших элементов.

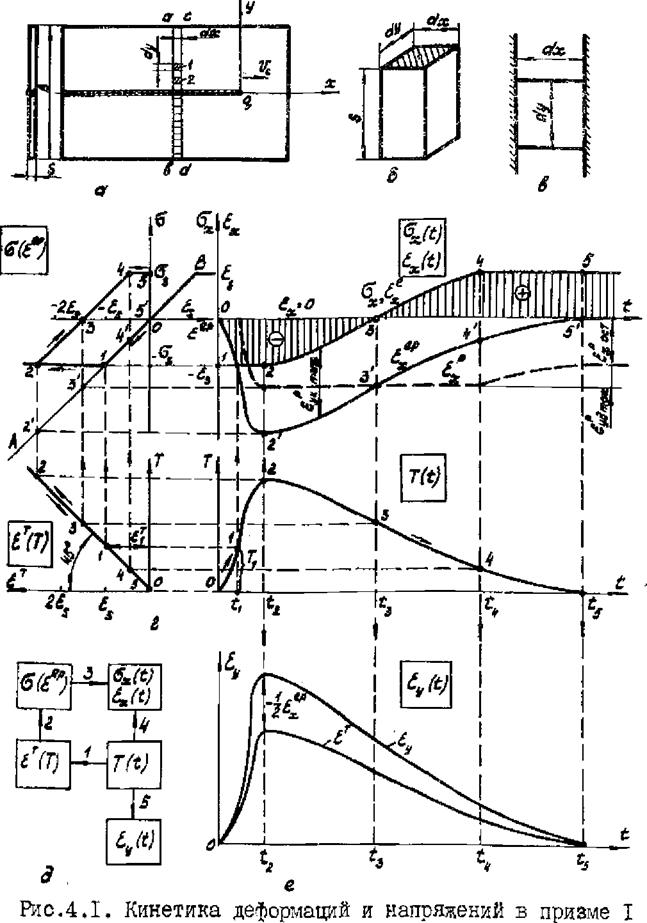
Под кинетикой деформаций и напряжений при сварке понима­ют процесс их развития в течение всего периода нагрева и остывания детали. Исследование кинетики сварочных деформаций и напряжений - проблема большой сложности, а решения возни - кающих при ее рассмотрении задач (в строгой постановке'' мо­гут быть выполнены, как отмечалось, только численными мето­дами. Шесте с тем физическая сущность процесса развития упругопластических деформаций при сварке достаточно - четко выявляется при его рассмотрения в рамках приняты) допущений.

При анализе температурного поля обычно строят кривые, характеризующие изменение температуры в данной точко с те­чением времени, т, е. рассматривают термические цикли точек, расположенных на разном расстоянии от оси коза. При анализе

термомеханических процессов важно проследить за изменением в указанных точках деформаций и напряжений. Пусть произво­дится сварка встык двух листов (наплавка валика на лист) на режиме, при котором неравномерностью нагрева по толщине мов­но пренебречь (рис.4.1,а), Выделим вдали от торцов двумя се - нениями at и сd полоску шириной dlx и разделим ее про­дольными сечениями на ряд элементов, каждый из которых будет представлять собой элементарную призму с основанием clxdy и высотой s (рис.4.1,6). Поскольку объем призм мал, можно считать, что в процессе нагрева п остывания температура каж­дой призмы одинакова по объему и изменяется во времени как температура ее центра тяжести. При обычной жесткости свари­ваемых элементов полные деформация вдоль оси ж, обусловли­вающие. фактическое изменение размера tlx „ значительно меньше температурных деформаций. лХ' Поэтому в первом приближении полными деформациями е, х можім пренебречь п полагать. что размер dx не изменяется (сечения аЪ я Ы не смещаются), т. е, что призмы находятся в условиях жесткого закрепления в направлении оси ж. (рио,4,!,в). При этом в процессе нагрева д посохе дующего остывания в призмах возникают и изменяются продольные напряжения 6Х. Б соответствия с допущением об одномерности напряженного состояния будем полагать, что на­пряжения 6^=0 , а следовательно, по направлению оси у де­

формации призм протекают свободно. Итак, в продольном на - правлении 6Е*0 , но ел-0 , а в

Для анализа деформационных циклов элементарных призм не­обходимо в качестве исходной информации иметь данные об из­менении объема металла вследствие тентового расшиоения (или фазовых превращений) и кривые деформирования металла для ря­да значений температуры (диаграмму растяжения-сжатия). Изме­нение объема металла при нагреве характеризуется дилатомет­рической кривой, получаемой на специальных приборах - дала - томвтрах, измеряющих дилатацию (свободное изменение линейно­го размера образца при нагреве). При отсутствии фазовых пре­грешений дилатометрическая кривая может быть эппроксимировв - 28 прямой (что означает постоянство коэффициента линейного расширения). Если принять также схематизированную диаграмму растяжения-сжатия (см. рис.2.3)* то анализ термодеформацион­ных циклов элементарных призм можно выполнить следующим мето­дом.

Изобразим схематизированную диаграмму растяжения-сжатия '•'"Д‘.ер) (рис.4 Л, г) в таком масштабе, при котором упругий уча-

,;ц; .диаграммы наклонен к оси еер под углом 45° (упругие

деформации и соответствующие. им напряжения характеризуются одинаковыми отрезками на диаграмме 6(е®р> . Под диаграгнмок расположим дилатометрическую кривую (в нашем случае прямую), мнбоав масштаб для дилатации равным масштабу деформации на

диаграмме б(&еР) , а масштаб для температуры таким, чтобы бы - ли павндаи отрезки, характеризущие температуру и соответ­ствующую ей дилатацию. Наконец, справа от дилатометрической кривой изобразим кривую термического цикла рассматриваемой :,";;измы, приняв для температуры тот же масштаб. Тогда кривые изменения во времени деформации, е. х“Еж+Еж и напряже­ний 6'х могут быть получены путем построения, показанного па. рис, 4 Л, г стрелкагли (ом. также схему построения на

0г;С.4Л, д), Например, для момента температура ТД харан - ■■■ариэуется точкой I на кривой термического цикла. Из этой

точки проведем горизонтальную прямую до дилатометрической кривой и получим точку I, которая характеризует свободную тем - : - тусную деформацию е.~ . При жестком закреплении призмы в...вправлений зо она определяет недопущенную. деформацию, поэтому, провод вертикальную прямую, получим точку I на

о-і or паше ff(eep') , которая и характеризует бх и 4 в мо - ■л.:нт t, (как видно из рисунка, в этот момент 6^=-^ ). Да - ■:se t путем переноса с диаграммы б(є®р') и кривой термическо­го цикла T(t) получаем точку I, принадлежащую искомой

метод принципиально но меняется, если использовать дейст­вительную дилатометрическую кривую (с учетом фазовых пре­во ащеюга' и отказаться от схематизации диаграммы растяже­ния-сжатия, т. е. использовать семейство опытных кривых декорыиоования металла (см. 4.7'1.

кривой изменения напряжений бх и упругих деформаций £х

од времени. Аналогично для момента времени to (момент мак­симального нагрева) температура, дилатация и напряжения ха­рактеризуются точками 2 соответственно на кривых термическо­го цикла, дилатометрической и диаграмме ff(eep) , Как видно

из диаграммы б(дер) , в этот момент имеет место упругая де­формация - es и максимальная пластическая деформация укоро­чения тах, соответствующая отрезку между точками I и 2. Отразим с помощь» прямой АВ упруг оплас типе с кие деформации с

плоскости б(еер) на ПЛОСКОСТЬ £x(t) . Для этого снесем точ­ку 2 на прямую Ай, получим точку 2* , которую к перенесем на

кривую продольных деформаций, т, е. суммарных упругих и пластических. На чертеже также показано построение характер­ных точек 3, 4, 5, В момент времени t, упругие деформации (напряжения) равны 0, в момент - ц начинается повторная пластическая деформация противоположного знака (удлинения), в момент t5 (полное остывание) пластическое деформации удли­нения соответствуют отрезку 4-5 на диаграмме 6(дер) , а оста­точные упругие деформации (удлинения) равны отрезку 5-51 на искомом построении. Таким образом, получаем кривые изменения во времени упругих деформаций ех (заштрихованные эпюры),

суммарных упругих и пластических деформаций ех и, как следствие, пластических деформаций е,^ (штриховая кривуш).

Отметгш, что ломаная линия 012345 на диаграмме 0'(еер) харак­теризует изменение напряжений в зависимости от температуры, так как шкалу дилатации можно рассматривать как температур­ную. Анализ полученных кривых позволяет заключить, что уп­ругая деформация укорочения к моменту ti достигает значения -£s и дальнейший нагрев призмы приводит, при неизменности упругой, к возникновению пластической деформации укорочения. Последняя к моменту максимального нагрева іг достигает наи­большей величины. Процесс остывания сопровождается сначала (до момента t5 ) разгрузкой (при неизменности пластической деформации уменьшается упругая), а затем нагрузкой, вызываю­щей в период от Ц до tj, рост упругой деформации удлине­ния, а в период от Ц до t5 - пластической деформации уд­линения. Из построения ясно, что пластическое удлинение (по­вторная пластическая деформация) возникает только при уело - вии l£v*. maxl>£-s или’ что то же сам°е* <^Тт>ге.5 (вариант,

рассмотренной! на рис,.4 Л, г). При этом остаточная пластиче­ская деформация не зависит от температуры максшального на - гоева и равна - tb, а остаточное напряжение - пределу теку­чести. Если это условие не соблюдается, а при нагреве возни­кает пластическая деформация укорочения, т. е. если призма расположена в зоне, где €,5<о1Тт<2,ц , то повторной пласти­ческой деформации нет, а остаточная равна той, которая воз­никла в момент максимального нагрева шах Зная

составляющие продольной деформации как функции времени по соотношению (2.7'', получаем кривую изменения полной попереч­ной деформации призмы (рис.4.1,е). Последняя примерно

в 1,5 раза превышает свободную температурную деформацию, и, разумеется, пренебрегать ею нельзя.

Аналогичное рассмотрение процесса развития упруго­пластических деформаций призмы 2, расположенной в непосред­ственной близости к оси шва, а именно в зоне, где Тт>Т*

( Тк - температура разупрочнения металла), выполнено ' на рис.4.2. Процесс развития деформаций этой призмы характерен тем, что в период нагрева выше температуры Т* металл нахо­дится в пластическом состоянии и напряжения отсутствуют. При остывании, начиная с температуры Т* , упругие свойства восстанавливаются и дальнейшее развитие процесса такое же, как и в рассмотренной призме I, Кривая (t) построена для t>tk.

При малой жесткости свариваемых элементов допущение об отсутствии полных деформаций в направлении оси х может при­вести к погрешностям. Поэтому рассмотрим тот же процесс де­формирования призмы, но в условиях, при которых свободная деформация призмы в направлении х ограничена не полностью, а частично. Пусть, например, деформация ех изменяется во времени* как показано на рис.4.3. Б этом случае построение искомых кривых выполняется так же, но недопущенная деформа­ция, опре делящая нг диаграмме <э (е&р) напряжения 5Х и де­формацию, равна ех~ ет . Это непосредственно следует

из уравнения (2.5), так как его можно переписать в виде

........ — ---------------

х) Функция. является искомой к учет полных деформаций

зыдолняют во втором приближении, полагая ь первом с. х(г)=о.

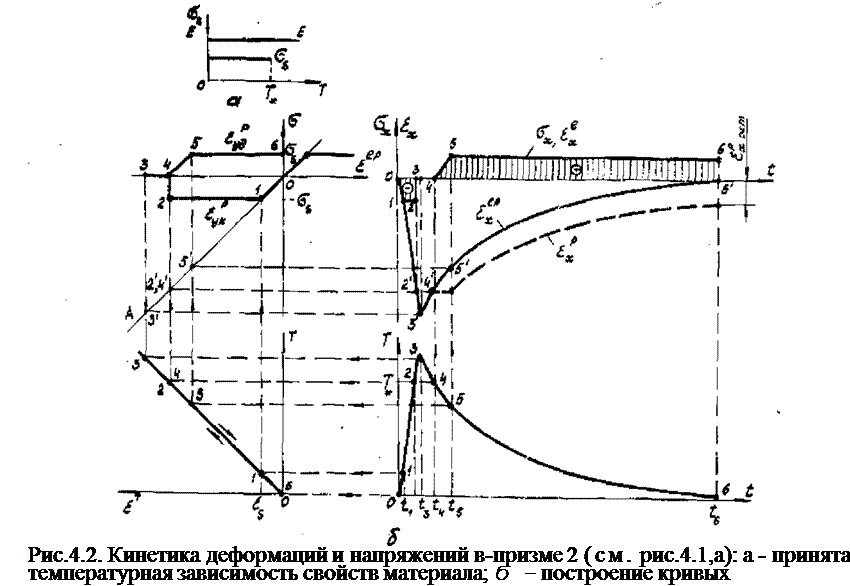Следовательно, от дилатометрической кривой нужно по го­ризонтали откладывать соответствуйте рассматриваемому мо­т-ленту полные деформации и лишь затем восстанавливать перпен­дикуляры к диаграмме <э(еер') . На последней пунктирной линии

показан характер изменения напряжений призмы при ее жестком закреплении. Видно, что учет tх привел к уменьшению плас­тических деформаций укорочения и удлинения. Первые уменьши­лись на, т. е. на полную деформацию в момент максі шаль­ного нагрева, а вторые - на гъ, т. е. на конечную полную де­формации- Обозначим их соответственно &хт и s. xotx • При жестком закреплении рассматриваемой призмы возникают по­вторные пластические деформации и напряжения достигают 6S, а при его отсутствия повторных пластических деформаций нет

остаточные напряжения С последние

точкой 3 на диаграмме 6 (е^ ).

Выполненный анализ кинетики упругопластических дефор­маций элементарных призм, нагреваемых по сварочным циклам, позволяет сделать следующие выводы.

1. В призмах, расположенных в зоне, где olTm>ts, при нагреве возникают пластические деформация укорочения.

2. В призмах, расположенных в зоне, где j..Tm>i£s, при остывании возникают повторные пластические деформации (про-

х) При учете полных деформаций указанные в выводах пределы повышаются тем значительней, чем меньше жесткость свари­ваемых элементов. Так, условия, указанные в выводах I, 2,

5, 7, имеют соответственно видд. тт>ьх+£хт-,дтт>ец^хт-,^ехт<<лт<

<гц+ехт ot (E. s+ex ослН&ДО (Зє-л+є-х^ їм. Уточняются также значения остаточных пластических деформаций, указанных в выводах 4 ;; 5. Они соответственно равны *£ocm=~t«>+ exocm и

ос. т~~(°^^т“2-хт + ^эс, оспп') •'

100

тивоположного знака).

3. Максимальные пластические деформации имеют место в момент максимального нагрева призмы.-

4. Если призма испытывает повторную пластическую дефор­

мацию, то, независимо от температуры ее максимального нагре­ва, остаточные напряжения, а остаточные пласти­ческие деформации •

5. Если призма расположена в зоне, где es<oLTm<£as то ее пластические деформации, достигая предельной величины в момент максимального нагрева, далее не изменяются и равны

~<^"^irn + e'S •

6. Конечное состояние призмы вполне определяется, если известно ее состояние в момент максимального нагрева. Поэто­му для оценки остаточных деформаций и напряжений изучение истории деформирования призмы можно ограничить двумя момен­тами времени; максимального нагрева'и конечным.

7. На точность определения остаточных деформаций и на­пряжений призмы оказывает влияние точность определения мак­симальной температуры, дилатометрической кривой и кривых деформирования только в интервале температур от es /<L до

. Точность определения максимальной температуры, а также характер указанных кривых (или их схематизация) выше указанного верхнего предела мало влияет на конечные резуль­таты.

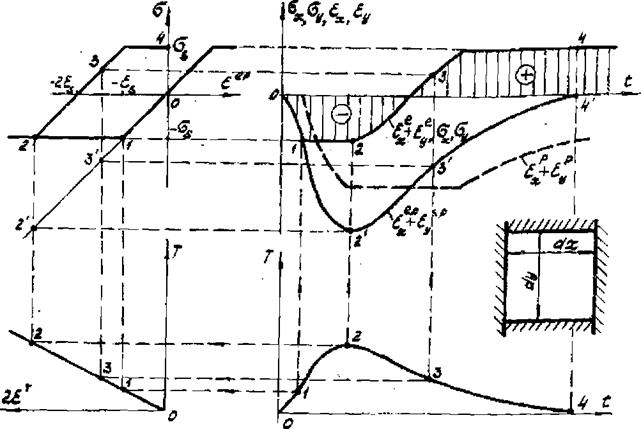
Прежде чем перейти к совокупному рассмотрению всех призм полоски, т. е. к изучению деформаций полоски в целом, рас­смотрим еще один вариант развития упругопластических дефор­маций элементарной призмы. Дело в том, что в ряде случаев (точечные швы, короткие провары и т. д.) допущение об одноос - ности напряженного состояния не оправдывается. Поэтому рас­смотрим процесс деформирования в результате нагрева-остыва­ния той же элементарной призмы, но жестко закрепленной в двух направлениях (рис.4.4). При таком закреплении призмы возникает "лоское напряженное состояние, но математически оно также является одномерным, так как в течение всего про­цесса 6ж=бу и равны между собой все составляющие продоль­ных и поперечных деформаций. Для анализа применим тот же метод построения кривых, но примем во внимание, что в данном

у4!

случае

*г£+^«гет-г-1Т t u*y)

где - e. t - приведенная деформация (интенсивность деформаций). В случае простого растяжения (сжатия) стержня tt <

Рис.4.4. Кинетика деформаций и напряжений в призме, закрепленной в двух направлениях

Следовательно, необходимо изменить вдвое масштаб на гра­фике дилатометрической кривой. Дальнейшее построение не имеет особенностей и выполняется так же, как на рис.4,1,г. Полу­чаемые кривые характеризуют напряжения и упругопластические деформации как в направлении оси ж, так и в направлении осп у. Из рис.4.4 видно, что закрепление призмы по двум направленням приводит к пластическим деформациям при более низком значении температуры (при T=e. s/£cі ). Если при одно­осного закреплении призмы пластические деформации и отличаются не только по величине, но и по знаку, то при дву - сеном закреплении они одинаковы в течение всего. процесса. Одноосное закрепление призмы будем называть полужесткой схе­мой, а двуосное - жесткой схемой процесса деформирования призм. J реальных условиях сварки эти схемы оправдываются в гой :лн иной мере, так как имеет место податливость окру-

х) Это положение доказывается в теории пластичности.

жавдего металла d обоих направлениях, т. е. возникают полные 'действительные) деформации £х и. При схеме ОДНООСНОГО закрепления призмы влияние податливости оценивается учетом полных деформаций е. х (при допущении гипотезы плоских сече­ний) , при схеме двуосного закрепления такой учет может быть выполнен методами теории термопластичности. Однако влияние податливости как при одноосной, так и. руосной схемах на ве­личину остаточных пластических деформаций незначительно, так как температурные деформации в области высоких температур значительно превышают полные деформации. х^ А именно в этой области формируются пластические деформации. Следует также отметить, что при обычных условиях сварки податливость в процессе нагрева уменьшает пластические деформации укороче­ния, в то время как при остывании ее... учет приводит к умень­шению пластических деформаций удлинения. Поэтому ее суммар­ный эффект весьма незначителен (за исключением некоторых особы:; случаев). Пренебрежение податливостью при оценке пла­стических деформаций, т. е. при решении термомеханической за­дачи, не исключает, а, наоборот, предполагает ее учет при решении деформационной задачи. В частности, при рассмотрении деформаций и напряжений в балках по формулам главы 2. Можно также использовать результаты решения термомеханической за­дачи для последующего решения деформационной задачи методами теории упругости.

Возвратимся вновь к полоске шириной dx, выделенной из пластины вдали от торцов (см. рис.4.1,а). Отнесем ее размер dx к единице длины, т. е. получим так называемую единичную полоску.

Изменение объема единичной полоски в направлении оси х в результате температурных и (или)пластических деформаций назовем погонным объемом продольного удлинения (укорочения) сварного соединения и обозначим vj1 , а его конечное значе­ние "irx.

Аналогично, изменение объема единичной полоски в на­правлении оси у в результате температурных и (или) пласти­ческих деформаций назовем погонным объемом поперечного уко-

х) Здесь не имеются в виду деформации в направлении оси у при одноосной схеме, т. е. при закреплении в направлении оси х. Они одного порядка (и даже больше) температурных и пренебрегать ими нельзя.

юз

рочения сварного соединения и обозначим ir^p, а его ко­нечное значение - .

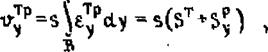В соответствии' с (4.32) и (4.23) можно зависать

где Ът - площадь эпюпы температурных деформаций но сечению пластины; Sp. - площади я шор соответственно продоль­

ных и поперечных пластических деформаций.

. Определение конечных значений указанных объемов, т. е. величин и Vy, составляют основную задачу настоящей главы. Но прежде чем приступить к ее выполнению, рассмотрит.! кинетику образования продольных и поперечных деформаций. Оче­видно, что она протекает одновременно. Однако исходя из ме­тодических соображений, рассмотрим сначала временные и оста­точные продольные, а затем - поперечные деформации и соот­ветствующие им объемные изменения металла.

Отметим также, что изучение процесса деформирования еди­ничной полоски не всегда сводится к простому суммированию процессов деформирования составляющих ее элементарных призм, рассмотренных изолированно. Возникает необходимость учиты­вать их взаимное влияние и обеспечивать основные принципы механики сплошных сред - соблюдение условий сплошности га лавновесия.