Свойства слоистых композиционных материалов
 29 ноября, 2012
29 ноября, 2012  admin
admin Анализ поведения слоистых композиционных материалов, состоящих из разнонаправленных слоев, может быть проведен на основе метода конечных элементов.
Каждый индивидуальный слой состоит из однонаправленных волокон, определяющих направление слоя, и матрицы, обеспечивающей нормальную и трансверсальную жесткость слоя.
Если нагружение слоя происходит не вдоль оси ориентации, он находится в состоянии послойного нагружения.
В соответствии с работой С. Цая и Н. Пейгано [5] соотношение напряжение—деформация для слоя может быть записано в виде матрицы
|
Ох ' |
"Qu |
Qi. |
Qxe" |
|||
|
Оу |
= |
Qn |
Qas |
Qze |
ЄУ |
|
|
„Qei |
Qm |
.Уху. |
Где ах, оуі аХгУ — напряжения, приложенные к слою; ев, е,, ?ху — деформации слоя;
Qu - зиг - f Ua cos 20 + Ui cos 49;
- зиг - f u2 + ua cos 20 + t/4 cos 49; Qu = Qu = Ui ~ U* — Ui cos 0; Qee = иг + U2 - f Ut cos 40;
QtІ = Qu = 4'Ua sin 20 + Ui sin 49;
Qea = Q«e = -5-u*sin 20 + u*sln 4e'
Где 9 — угол между осями ориентации слоя и образца. Кроме того,
Ul = "8^"Е22 V*lEu
U* = - ЩГ — "Г + VI2Ј22)] ;
UІ = - щ - [Еп + Еп — (v21Ј11 + v12Ј22) - Цв1г],
Где £и, Е2і, Gn — продольный, поперечный (трансверсальный) и сдвиговый модули упругости слоя; v12 — главный коэффициент
309
Пуассона; val — второстепенный (поперечный) коэффициент Пуассона; г|? = = 1 — vuvei.
В соответствии с теоремой Максвелла имеем
V12ei2 = v21Јu.
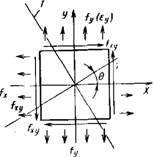
Традиционные направления напряжений в плоскости слоя приведены на рис. 20.7.
Большинство типов структур подвергаются сложному нагружению, меняющемуся от точки к точке. Так как ориентация волокон внутри слоя не может быть изменена без разрушения волокна, ориентация однонаправленных слоев в композите осуществляется в четырёх основных направлениях (0°, 45°, 90°, —45°), составляющих четыре основные группы. Ламинаты внутри каждой из таких групп могут быть созданы со свойствами, близкими к оптимальным. В зависимости от требований число слоев каждого вида может варьироваться. Относительно биссектрисы угла между осями ориентации слоев +45° и —45° существует ось симметрии. Это уменьшает возможность коробления композита, которое с большой вероятностью возникает при создании несимметричных ламинатов.
Для уменьшения напряжений в матрице (в связующем) и обеспечения максимальной реализации свойств волокон слои должны быть ориентированы минимум в трех направлениях: 0°, +45°, —45°. В большинстве конструкций используются слоистые композиты с ориентацией слоев во всех четырех направлениях. Это позволяет минимизировать напряжения в матрице и создавать наиболее благоприятные условия поведения композита.
В данной главе, посвященной конструированию и анализу структур материалов, будут рассмотрены слоистые композиты с ориентацией слоев во всех четырех направлениях и парных слоев (+45°, —45°).
|
Рис. 20.7. Направление напряжений в слое: |
|
1 — ось ориентации поперек слоев, Ец 2 — ось ориентации вдоль слоя, Ец |
Рассмотрим ламинаты с ориентацией (0°, 90°, ±45°) и равным числом слоев в направлении ±45°. Коэффициенты упругости для каждого слоя приведены в табл. 20.4.
|
(20.2) |
Используя L, М и N для обозначения вклада (числа) каждого из слоев с ориентацией соответственно 0°, 90° и ±45°, суммируя деформации в плоскости слоя и используя условие равновесия, получаем
La* + MoT + No? = ах; Lay + AfaJ* + NaNy = <r„; Low + N a xy = oxy,
20.4. Коэффициенты упругости в уравнениях зависимости - напряжение — деформация для слоев с различными углами ориентации
|
90" |
|
±45' |
Коэффициент
|
Qa |
ЈUA|) |
Ejy |
|
Qn |
Ejy |
Eii/rJ» |
|
Qu |
VtaEM/$ |
|
|
Qee |
Git |
Gii |
|
Qie |
0 |
0 |
* Для слоев ±45° коэффициент Qee используется в виде среднего значения модуля упругости при растяжении и сжатии Elt и £22, т. е. £п ср = (£ц +
+ £22)/21 £22ср = (£22+ ^и)/2-
Где ох, а„, аху — соответственно продольные, трансверсальные
L М
И сдвиговые напряжения в ламинате; сг^ и а{/ — напряжения в направлениях 0 и 90° соответственно; Оц— напряжения в слоях с ориентацией ±45°.
Объединяя (20.1) и (20.2), запишем
*, = (£ TfQu)E,+ (Ј #Q?2)Є, = Аигя + А12Є»;
А„ = (2 RQn) е„ + (Е RQ&) 8Р = А12ех + Л22е,; (20.3)
Охд = ( S RQgg) Ухе = АбвУхд,
Где JjRQ? i — суммирование по слоям данного направления по всей толщине материала, так что
ZRQft =LQ?, + MQ? i + JVQji; Atj — коэффициенты жесткости ламината.
Преобразуя уравнения (20.3) относительно деформаций, имеем
Е„ =
1 [splits' ( '
_ аху
УХУ " £
|
20.5. Упрощенные коэффициенты упругости в уравнениях зависимости напряжение — деформация для слоев с различными углами Ориентации
|
Упругие характеристики слоистых материалов могут быть получены из следующих соотношений:
Уху*ух
А22 = АУ=
|
Ап |
|
= S Я(2& |
1 — v*yvyx
Л12 =
F — VxyVy»
Лбб = Лw = GXy = s v
*f ~ S '
"" M'
Напряжения, возникающие в каждом слое, можно получить из уравнений 20.4 и 20.1:
* [of, S ~ Q.2 £ - [ей S - eg S.
|
(20.5) |
|
12, |
|
On = |
.і? _ - s - Qia S q* + [^2 s ^Qn - Qia a °y
1 — Wi/x
CTjey =
Наибольшая сложность использования этих соотношений для анализа и конструирования материалов заключается в необхо - 312
Димости знания очень большого числа параметров. Кроме того, накладываются и различные внешние влияния — например, изменение температуры. По крайней мере, семь основных величин для материала должны быть известны для каждой температуры. Величины Еп (£пр), <*в1, аст и v12. являющиеся В СЛОЄ соответственно продольным модулем упругости, пределом прочности при растяжении, пределом прочности при сжатии и коэффициентом Пуассона, незначительно зависят от температуры. Однако значения £Поп. Gn> Ga и G66 (соответственно поперечный или трансверсальный) модуль упругости, модули сдвига в плоскости слоя и два межслоевых модуля сдвига) существенно зависят от температуры, так как определяются свойствами матрицы.
|
К О Л 0,2 |
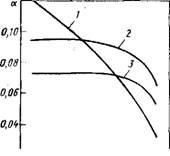
Для предварительных конструкторских разработок расчеты должны быть упрощены, например, если допустить максимальную ошибку для эпоксиборопластиков (ЭБП) равной 10 %, а для эпоксиуглепла -
|
|

 Опубликовано в
Опубликовано в