СВАРИВАЕМЫЙ КОНТАКТ. И ПРОЦЕССЫ ЕГО АКТИВАЦИИ
 26 февраля, 2016
26 февраля, 2016  admin
admin 1.1. Структура и геометрия металлических поверхностей
В технологии машиностроения занимаются лишь геометрией металлических поверхностей. Для сварочной технологии кроме геометрии необходимо исследовать физические процессы, которые происходят на поверхностях свариваемых деталей. Процессы эти разнообразны, динамичны и очень сложны по своей физической природе. Для сварочной технологии, на современном ее этапе, полезно рассмотреть все, что происходит на поверхности металла от момента ее подготовки к сварке до самого сварочного процесса. Наиболее удобно анализировать поверхностные явления на металле, используя следующую модель. Представим себе, что разрываем металлический образец. До разрыва внутренние слои металла были абсолютно свободны от всяких посторонних загрязнений. Они были построены в виде нормальных кристаллических структур, с обычными для реального металла дефектами. Поверхность разрыва в момент ее образования идеально чиста. Такую чистоту называют ювенильной. Обнажающиеся при разрыве кристаллические грани элементарных кристаллов особенно и необычайно подвижны. В первые же миллионные доли секунды большая часть свободных электронов покидает кристалл и образует над его гранями подвижное отрицательно заряженное облако. Вслед за этим эффектом, а затем и одновременно с ним все острые кристаллические грани размываются, придавая острым выступам округлые очертания: при выравнивании и закруглении рельефа поверхностная энергия уменьшается.
Электронное облако над поверхностью и избыточный положительный потенциал кристаллов создают прочный и стойкий двойной электрический слой (рис. 1.1, а). Такой слой может существовать только в абсолютном вакууме. Если же разрыв металла произошел на воздухе, то двойной пограничный слой может возникнуть только как первый импульсный эффект. Электронное облако без промедления (рис. 1.1, б) активирует молекулы кислорода в окружающей атмосфере, которые с большой скоростью образуют оксидную пленку. Электрическая структура пленки непрерывно сохраняет разнополярность внутреннего и наружного слоев. Если первый электронный слой возникает мгновенно, то он мгновенно же вступает во взаимодействие е молекулами кислорода, активи-
зируя их на образование химической связи с металлом. Над поверхностью металла образуется рыхлое и подвижное облако ионов металла, его оксидов и свободных электронов. В этом облаке самой активной составляющей и притом длительно, в течение минут и даже десятков минут, остаются свободные электроны. Электронная эмиссия с металлической поверхности за это время продолжается даже сквозь слой уже образовавшегося оксида (рис. 1.1, в). В земной атмосфере при избытке кислорода мономолекулярный слой кислорода на поверхности только что разорванного образца выстраивается за миллиардную долю секунды, при давлении КГ6 мм рт. ст. — за 2 с, при давлении 10~8 мм рт. ст. — за 30 мин, в космическом вакууме — за 7 лет. Созданная на реальном металле оксидная пленка не остается непроницаемым и мертвым панцирем. Она сама по границе ее с металлом и по границе с окружающей средой весьма длительно живет подвижной электрической жизнью, если даже на нее не воздействуют никакие механические силы. Образовавшийся оксидный слой непрерывно обменивается с металлом электрическими зарядами. Верхний слой металла, на котором образуется оксидная пленка, представляет собой особую физическую систему, поскольку любая механическая обработка создает в этом слое полностью разрушенную и разориентирован - ную кристаллическую структуру. Глубина таких слоев зависит от способа механической обработки: после тонкого шлифования — приблизительно от 2 до 25 мкм, после точения и грубого шлифования — от 75 до 250 мкм, после полирования — от 0,2 до 0,5 мкм. Энергетическая и электрическая пересыщенность таких слоев по сравнению с нормальной структурой металла весьма велика. Это и проявляется в необычайно высокой активности, с какой на такой поверхности возникают оксидные наслоения, с которыми и приходится особенно считаться технологу при различных способах сварки давлением.
![]()
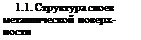
 Начальные скорости окисления обнаженных металлических поверхностей, как уже указывалось, огромны. Однако по мере увеличения толщины оксидного слоя на холодном металле стабилизируются пленки такой сравнительно небольшой толщины, что металл визуально сохраняет свой характерный металлический блеск. Такие оксидные наслоения благодаря их малой толщине оптически прозрачны. Так, в частности, если говорить о железе, то его металлическая поверхность не теряет своего блеска, пока
Начальные скорости окисления обнаженных металлических поверхностей, как уже указывалось, огромны. Однако по мере увеличения толщины оксидного слоя на холодном металле стабилизируются пленки такой сравнительно небольшой толщины, что металл визуально сохраняет свой характерный металлический блеск. Такие оксидные наслоения благодаря их малой толщине оптически прозрачны. Так, в частности, если говорить о железе, то его металлическая поверхность не теряет своего блеска, пока
|
Цвет побежалости |
Температура возникновения, рС |
Приблизительная толщина слоя д. І0». см |
|
Соломенно-желтый |
220—240 |
450 |
|
Оранжевый |
240—260 |
500 |
|
Красно-фнолетовый |
260—280 |
650 |
|
Синий |
280—300 |
700 |
|
Окалина |
600 |
5000 |
толщина оксида не превышает 3-10"8 м. Можно заметить отсюда, что даже самое мелкое зерно, какое может быть в полированном слое (0,2 мкм), в семь раз превышает толщину оптически прозрачного оксидного слоя 0,03 мкм. Разумеется, нагрев металла при его механической обработке может заметно увеличить толщину оксидного слоя. Известно, в частности, что с повышением температуры поверхности на железе появляются цвета побежалости (табл. 1.1).
Электрическая структура оксидов многих металлов чисто полупроводниковая. Наслоения оксида на металлической поверхности имеют более сложную переходную структуру от металлического проводника к полупроводнику. Поверхностный слой разориенти - рованных кристаллов по своей электрической структуре иногда ближе подходит к полупроводникам, чем к металлу.
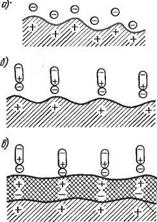
Рассмотрим геометрические характеристики механически обработанной металлической поверхности. Геометрию металлической поверхности исследуют и изучают в различных масштабах. Если масштаб макроскопический, то п’оверхность характеризуется степенью ее волнистости. В пределах каждой волны поверхность в зависимости от способа обработки обладает той или иной шероховатостью (рис. 1.2). Шероховатость в технологии машиностроения моделируют в виде различных геометрических фигур. В этой книге шероховатость принято моделировать пирамидами с квадратным основанием (рис. 1.3). Волнистость измеряется обычными инструментами (линейками, штангенциркулями), шероховатость очерчивают особые приборы — профилографы. Одна из типовых профилограмм показана на рис. 1.4. Каждая пирамида построена из множества разрушенных кристаллитов (рис. 1.5) и оказывается насыщенной огромным числом дефектов решетки. В сумме все разрушенные кристаллические организации и являются теми концентраторами избыточной энергии, за счет которой весьма активно оксидируется металлическая поверхность. Структура Двойных электрических слоев повторяется и на поверхности оксидных пленок (рис. 1.6). Воздушная среда цеха обеспечивает адгезионные наслоения на оксид водяных, масляных и пылевых частиц, каждая из которых всегда электрически полярна.
п
|
|
|
|
Как видно, металл надежно защищает чистоту своих глубинных слоев. Оксидные и адгезионные наслоения и являются главным препятствием против самопроизвольного сваривания любых металлических поверхностей, образующих контакт. Электрическая связь адгезионных и оксидных наслоений с металлом очень прочна.
Зачистка всех наслоений с поверхности металла практически невозможна никакими химическими, физическими и механиче-
|
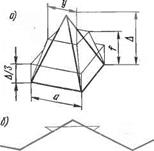
Рис. 1.4. Профилограмма поверхности алюминиевой пластины после зачистки ее наждачной бумагой (с) и в результате ее деформации плиткой Иогансона поддавлением 20,100 и 200 МПа (б)
|
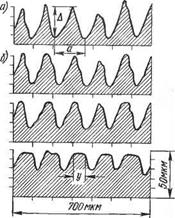 Рис. 1.5. Микроструктура пирами-
Рис. 1.5. Микроструктура пирами-
дальной шероховатости
Рис. 1.6. Схема строения слоев на
реальной металлической поверхно-
сти:
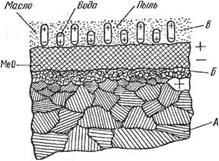 А — металл глубинных слоев; Б металлооксидная евтектика внешнего кристаллического слоя; В — адсорбционные наслоения по оксидному слою (воздух, пары воды, масло, пыль); МеО —’ оксидный слой (толщина относительно увеличена)
А — металл глубинных слоев; Б металлооксидная евтектика внешнего кристаллического слоя; В — адсорбционные наслоения по оксидному слою (воздух, пары воды, масло, пыль); МеО —’ оксидный слой (толщина относительно увеличена)
скими средствами. Всякая, даже самая тщательная, зачистка металлических поверхностей способна только свести к минимальной толщине все оксидные и адсорбционные наслоения на поверхности металла. Контакт двух металлических деталей без промежуточной оксидной и адсорбционной прослойки, т. е. непосредственно контакт между кристаллами может быть обеспечен только в двух случаях:
1) когда контакт осуществляется в космическом вакууме;
2) когда пластическая деформация выдавливает и выносит за пределы плоскости контактирования все оксидные и адсорбционные наслоения.
К последнему, идеальному случаю с различной степенью успеха стремятся все технологические приемы всех процессов сварки давлением.
Что касается процессов сварки плавлением, то здесь все оксидные и другие наслоения просто растворяются в расплавленном металле. Удаление загрязнений металла в одних случаях и растворение этих загрязнений в других — вот в этом и есть одно из самых существенных различий между сваркой давлением и плавлением. Как будет показано в дальнейшем, при современной контактной точечной и шовной сварке соединения образуются по принципам плавления.
На рис. 1.4 представлена картина постепенной деформации выступов шероховатости при сдавливании этих выступов плиткой Иогансона, т. е. почти идеально плоской деталью. Наибольшее давление (200 МПа) значительно превышает предел текучести отожженного алюминия. Тем не менее пирамиды полностью не смялись и не превратились в параллелепипеды. Этот факт объясняется следующими причинами.
Поверхностный слой металла в результате любой механической обработки становится предельно наклепанным, насыщаясь линейными и точечными микродефектами в сотни и тысячи раз больше, чем это характерно для нормального проката. Оксидные прослойки проникают в глубину шероховатостей, создавая своеобразную эвтектику металла с его оксидами (слой Б на рис. 1.6). Показатели микротвердости, приведенные в табл. 7 приложения,
определяют, насколько может повыситься микротвердость пирамид в целом, если их структура из чисто металлической превращается в металлооксидную. При значительных давлениях в порах, образующихся между пирамидами, сжимаемый воздух настолько нагревается, что должно произойти энергичное окисление металла, окружающего поры. Этот эффект вызывает еще большую концентрацию оксидной фазы в металле и соответственно повышает и показатели твердости, и значения удельного электрического сопротивления поверхностного слоя металла. В табл. 7 приложения приведены сравнительные значения удельных электросопротивлений некоторых металлов и их оксидов. Сравнивая эти данные, можно сделать вывод, что и с точки зрения электропроводности шероховатая поверхность металла по своим свойствам может значительно приближаться к полупроводникам.
Учитывая изложенное выше, следует констатировать: в земной атмосфере никакие металлические поверхности не могут быть свободными от оксидных и адсорбционных наслоений. Весь вопрос для сварщиков сводится только к тому, какова структура и толщина этих наслоений. Несмотря на неизбежное наличие поверхностных наслоений, в технологической практике используются термины «чистого металла» в смысле его зачистки перед сваркой. Для контактной сварки визуальная оценка чистоты определяется отсутствием явно видимой окалины или явно видимого потускнения. С этой точки зрения идеальной поверхностью считают холодный прокат, протравленный металл, металл, зачищенный абразивным инструментом и абразивным материалом.
Выше было определено, что главной и даже единственной причиной неизбежных оксидных и адсорбционных наслоений на поверхности металла является факт энергетического неравновесия, энергетического контраста между средой и вновь образовавшейся поверхностью металла в этой среде. Электрическая полярность всех слоев на металле, показанная на рис. 1.6, говорит и об электрической природе всех границ структур, что подтверждается многими измерениями разности потенциалов. Установлено, например, что не только два соседних кристаллита энергетически неравновесны, но даже граница зерна по сравнению с его серединой электрически более отрицательна. Упругие деформации почти не изменяют разности потенциалов между соседними зернами, пластические же сказываются в очень сильной степени. Все надрезы, трещины и другие концентраторы напряжений дают отрицательный потенциал относительно основной массы металла.
Любые соседние контрастные элементы структуры, любые два соседних зерна одной и той же структуры, но разного размера, два различно деформированные зерна обязательно имеют между собой электрическую разность потенциалов как следствие электрической природы строения вещества.
Эти общеизвестные факты почти не используются, к сожалению, металловедами при изучении металлических структур.
Для технологов сварочного производства отмеченные микро- электрические эффекты существенны, особенно при изучении контактных сопротивлений. Вероятно, существует прямая связь между явлением экзоэлектронной эмиссии и фактом медленного выравнивания разности потенциалов между различно деформированными объемами металла.
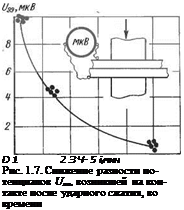 Максимум экзоэлектронного выхода наступает через несколько минут после момента пластической деформации. Падение электрического потенциала £/ю от максимума до нуля на холодном контакте во времени от момента контактирования также происходит за минуты (рис. 1.7).
Максимум экзоэлектронного выхода наступает через несколько минут после момента пластической деформации. Падение электрического потенциала £/ю от максимума до нуля на холодном контакте во времени от момента контактирования также происходит за минуты (рис. 1.7).
Механическая деформация шероховатостей — это акт некоторой общей для контакта атомно-электронной активации, которая за несколько минут постепенно угасает, создавая равновесную электрическую структуру. Это и фиксируется, в конечном итоге, нулевой разностью потенциалов на холодном контакте. Получается некоторый физический парадокс: механический контакт при своем возникновении оказывается чисто электрическим. Другое дело, что разности потенциалов на нем измеряются микровольтами, что весьма мало по сравнению с теми, что возникают на контакте при прохождении через него сварочного тока. Тем не менее для объяснения электрического пробоя через поверхностные слои на металлических поверхностях в контакте вряд ли следует пренебрегать явлением его своеобразной электризации путем давления. Наиболее достоверно считать, что в плоскости всякого механического контакта в момент его организации за счет энергии пластической деформации образуется структура плазмы, и плазмы безусловно проводящей, если этой проводимости не мешают большие толщины оксидов.
Оксидная пленка на рис. 1.6 показана схематически и увеличенной толщины. Ее сцепление с металлом происходит через промежуточный разориентированный слой оксидно-металлической эвтектики. Наличие такого слоя в плоскости холодного контакта неизбежно при любой толщине оксидной пленки. Рассматривая профилограмму поверхности на рис. 1.4, можно сопоставить относительные размеры пирамид шероховатости и толщины оксидной, оптически прозрачной пленки на пирамидах. Если высота пирамиды приблизительно 50 мкм, а толщина пленки 0,03 мкм, то из рис. 1.4 можно увидеть, что высота пирамиды в тысячи раз больше толщины оксида на ней. Таким образом, макрошлиф реального
холодного контакта свежезачшценных деталей покажет толщину оксидной пленки, разделяющей детали приблизительно такого же размера, как и толщина межкристаллитных границ. Однако структуры этих двух границ категорически различны, так же как различно строение самой пирамиды и внутреннего зерна металла.
Зерна (кристаллиты) составлены из фрагментов, фрагменты — из блоков. Блоки как группа элементарных кристаллов могут быть разориентированы (а не разделены прослойками) относительно друг друга на доли градуса, фрагменты — на несколько градусов. Внутри зерна никаких оксидных загрязнений нет, но зерна отличаются друг от друга не только ориентацией, они отделяются особыми межкристаллитными границами. Эти границы оказываются насыщенными всеми возможными несовершенствами кристаллических решеток. Тем самым межкристаллитные границы представляют собой концентраторы особой энергии, всегда стремящейся к возможной разрядке. Разрядка может происходить в виде высокой химической активности границ по сравнению с серединой зерна.
Общеизвестное явление повышенной скорости травления меж - зеренных границ для сварщиков-технологов должно быть подчеркнуто особенно. Протравленная межзеренная граница своей чернотой создает впечатление полной разобщенности зерен и тем самым якобы подчеркивает полное отсутствие прочностной связи между ними. В действительности между зернами существует сильнейшая металлическая связь. Зерна посредством больших пластических деформаций могут дробиться на множество более мелких, показывая при травлении свои новые границы. Эти границы при последующей рекристаллизации исчезнут в процессе поглощения одного зерна другим. Новые границы снова будут визуально фиксироваться как черные изолирующие прослойки. Однако эти прослойки никогда не вызывают у исследователя сомнений в прочности металла по межзеренным границам, поскольку известно, что во многих случаях здесь оказывается большая прочность, чем в сердцевине зерна.
Некоторые процессы контактной сварки (особенно микросварки) протекают при температурах ниже точки плавления. При этом достигаются высокие прочностные свойства соединений, но в разрезе соединений на макрошлифах также видна протравленная сплошная чернота по плоскости контакта. Вот эта чернота в сваренном контакте почему-то у многих металловедов вызывает подозрение в непроварах. Можно вполне определенно утверждать, что и по плоскости сваренного контакта визуально заметная граница только потому и оказывается заметной, что здесь в процессе сваривания произошла обильная концентрация микродефектов всех родов. Это вызвало активную химическую реакцию травления, что и зафиксировалось черной прослойкой, видимой на макрошлифе.
Вопросами теории холодных контактов металлических поверхностей задолго до сварщиков занимались технологи машиностроения. В этой области накоплен большой опыт, который и следует позаимствовать для контактной сварки, но если речь идет только о холодном контакте, находящемся под статическим давлением.
Показатели шероховатости после различных видов механической обработки поверхностей представлены в табл. 5 приложения. Здесь же даны значения коэффициентов b и v, введенные в практику Н. Б. Демкиным и И. В. Крагельским [31.
Как было ранее обусловлено, шероховатость моделируется в виде пирамид с квадратным основанием. Моделирование такого рода безусловно идеализировано, но без систематизации размеров и форм шероховатостей невозможны никакие расчеты и даже качественные выводы. На основании конкретных значений шероховатости можно сделать вывод, что при всех видах обработки пирамиды представляют собой сильно сплюснутые геометрические фигуры: размеры основания в десятки или сотни раз превышают высоту пирамид. Такая форма выступов определяет разную деформационную картину в зависимости от программы приложения действующего давления и температуры пирамиды.
Для ударного давления плоской пластиной по холодной пирамиде она получает деформацию по схеме рис. 1.3, б. Нагретая целиком под действием статической или медленно изменяющейся силы пирамида деформируется по схеме рис. 1.3, в. Такого рода деформации характерны только для сил, сдавливающих пирамиду от ее вершины точно по оси симметрии. Однако практически почти при всех способах сварки давлением осевое давление сочетается со сдвиговым в какую-либо сторону. Мало того, и чисто осевое давление в свариваемом контакте как в отдельных микропирамидах, так и по всей плоскости контакта всегда завершается сдвиговым эффектом. Как будет показано в дальнейшем, этот эффект является самым главным фактором формирования сварного соединения вообще.
Для равномерной осевой деформации при полном смятии пирамида превращается в параллелепипед. Частичная деформация создает идеализированную усеченную пирамиду. Единичную площадь контакта смятой пирамиды у2 принято обозначать так:
У2 = Mr - (1-1)
В плоскости реального металлического контакта (рис. 1.8) мо
жет образоваться п таких площадок. Если считать все АЛ, одинаковыми, то в сумме они составят так называемую фактическую площадь контакта
А, — пААг. (1.2)
Фактическая площадь контакта — это в значительной мере
показатель поверхностной шероховатости, но не только. Чис-
ло элементарных. площадок п определяется и волнистостью контактируемых деталей (см. рис. 1.2). В связи с этим введено понятие контурной площади контакта. Эту площадь обозначают Ас и ее размер определяют теми границами, в пределах которых вписываются все элементарные площади контакта ААГ.
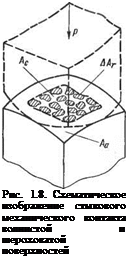 Размер площади сечения всей свариваемой детали, или размер предельно возможной площади контактирования деталей, называют номинальной площадью контакта и обозначают символом Аа.
Размер площади сечения всей свариваемой детали, или размер предельно возможной площади контактирования деталей, называют номинальной площадью контакта и обозначают символом Аа.
В технологии машиностроения принято определять относительную деформацию единичной пирамиды следующим образом (см. рис. 1.3):
—-Т1-1— / = Д (I -«)-
(1.3); (1.4)
Относительную деформацию группы микропирамид, составляющих фактическую площадь контакта, согласно экспериментальным данным Н. Б. Демкина [3 ], принято вычислять так:
Е — ІР/(Рс. д&)]1/у< (1.5)
В этой формуле козффи шенты Ь и v характеризуют деформационную способность шероховатой поверхности чисто геометрически, без учета способа обработки поверхности ее физического состояния; р — давление, усредненное по контурной площади контакта; рс. д — сопротивление деформации микропирамид, это показатель в значительной степени неопределенный, его величина зависит от способа обработки поверхности металла и энергии, с какой это делалось.
В технологии машиностроения величину рс. д для всех видов станочной обработки рекомендуют принимать, в среднем, равной тройному пределу текучести металла
Опыт показал, что для свариваемых контактов при точечной и стыковой сварке это соотношение дает удовлетворительные результаты при расчетах площадей контактирования.
Контактные площади определяются критериальным числом [7]
где 0 — температура металла в зоне контактирования; 0ПЛ — температура плавления.
Контурная площадь контакта определяется 17] в зависимости от критерия деформационного подобия Z по формуле
Д, = Д,(1 —e~z). (1.8)
При Z я* 4Лс я» Аа в холодном контакте при 0 = 0ХОЛ такое равенство может наступить при р — р0.п.
Тогда» приравнивая
^ПЛ
определяем коэффициент
а~4ввл/вхоя. (1.9)
Подставляя его в формулу (1.7), получаем значение критерия Z как для холодного, так и для горячего контактов
2 = 4р8/(рс. д8хол), (1-Ю)
где 0хол! — комнатная температура, равная примерно 300 К; 0 — температура горячего металла в зоне контактирования. Значение рс. д можно принимать по соотношению (1.6), т. е. равным тройному пределу текучести.
Если контурная площадь под действием давления и нагрева стремится в пределе к номинальной, то, видимо, фактическая площадь имеет своим пределом контурную. Закономерность изменения фактической площади под действием давления и нагрева, очевидно, также должна определяться критериальным числом, аналогичным Z. В [71 он был обозначен символом X и определен следующими соотношениями:
для грубообработанных поверхностей, когда значение показателя степени в формуле (1.5) принимается равным двум (см. табл. 5 приложения), критерий X равен
XVr~2 — 0др/(28
для тонкой (чистой) обработки при v — 3
X-v—ъ = 0дР/(8холСгтЬ). (1.12)
Для холодных контактов, когда температуру выступа можно считать 8д = Охоаг эти формулы соответственно принимают вид:
XV4=2 = р/(о*2Ь); Х^ - рЦаф), (1.13); (1.14)
где стт — предел текучести металла в предельно наклепанном состоянии (при деформации 80—90 %). Коэффициент Ь приведен в табл. 5 приложения.
Фактическую площадь контакта определяют по формуле
' Лг = Лс(1-е~х). (1.15)
Формулы (1.11)—(1.15) полностью достоверны для машиностроительных контактов, в которых все деформационные, струк-
19
|
Рис. 1.9. Схемы распределения напряжений по плоскости контактирования в статических механических контактах |
турные и, следовательно, электрические микропроцессы успокоились и стабилизировались. Для свариваемых контактов в моменты их образования определение площади весьма затруднительно, особенно при действии ударных сдавливающих сил. Для такого рода нагрузок на контакт значения величин ре. д, ат, входящих в структуру критериев Z и X, могут заметно различаться в зависимости от программы приложения давления, действующего на контакт и, следовательно, в зависимости от мгновенной концентрации энергии в плоскости контакта.
Вопросам концентраций и распределения действующих механических напряжений посвящено много литературы. Для условий контактной и некоторых других процессов сварки давлением схемы силового взаимодействия представляют значительный интерес. о_
На рис. 1.9 показаны эпюры распределения механических напряжений по плоскостям контактирования и плоскостям резкого изменения сечений.
Для практических расчетов принимают, что под абсолютно жестким пуансоном (рис. 1.9, а) абсолютно жесткая плита равномерно нагружается силой Р, т. е. полагают, что
р ■-= Р/(яг2).
В действительности распределение давления происходит по закону
p-^-L-L 1 (1.16)
Уг 2 пг9 і xi/ri
Формула (1Л6) дает теоретически бесконечно большие значения давления по образующей цилиндрического пуансона. Практически идеально жесткого пуансона не бывает, так же как не бывает пуансона хотя бы без самых малых закруглений по краю опорного круга 1—1 (рис. 1.9, а). При наличии таких закруглений кривая распределения давлений также превращается в закругленную: кривая 2—2 (рис. 1.9, б). Если плита сама оказывается к к тому же не абсолютно жесткой, а обладает пластичностью, то кривая давлений резко меняет свое очертание, превращаясь в кривую 3—3. По этим кривым, в согласии с формулой (1.16), Видно, что в центре, по осевой линии пуансона, во всех случаях действует давление
Рп = 0,5Р/(яг*) (1.17)
или несколько меньшее этой величины. На рис. 1.9, в показано внедрение пуансона в металл (прошивка металла). Стрелки показывают течение слоев металла радиально осевой линии пуансона. Для определения действительных напряжений в металле при деформировании по схеме рис. 1.9, в существует известная формула Е. П. Унксова
°-,’’[1 + 6(гаГ + 1п-т]- 0-18)
Как видно из формулы (1.18), для прошивки металлической болванки толщиной 6 и диаметром D необходимо создать напряжения сжатия, превышающие предел текучести на некоторый коэффициент (приведен в квадратны* скобках), зависящий от размеров заготовки и глубины проникновения пуансона. Первые два члена этого коэффициента показывают, какие должны быть приложены давления, чтобы деформировать цилиндрическую заготовку abed (рис. 1.9, в) без окружающей ее массы металла. Вторая часть коэффициента, In (D/d), определяет увеличение доли тех напряжений, которые действуют радиально, вызывая распор металла.
Рассмотрим некоторые схемы пластической деформации при стыковом контакте.
Если сжатию подвергается целый стержень из жесткого, непластичного металла, то никаких пластических деформаций нет, и эпюра действующих напряжений сжатия представляется в виде равномерно распределенной нагрузки (рис. 1.9, г). Если на стержне из такого же жесткого материала сделан кольцевой вырез (или два идеально подогнанные друг к другу по плоскости контакта стержня, которые по краю не соприкасаются) (рис. 1.9, д), то у вершины выреза концентрируются пиковые напряжения. Если целый стержень из пластического металла деформируется между двумя плитами, в которых он жестко закреплен (абсолютное трение), то распределение напряжений сжатия представляется эпюрой, изоб-
(1.19)
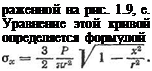 При стыковой сварке двух стержней (рис. 1.9, ж) эпюра действующих давлений на практике оказывается более сложной, чем для целого стержня (рис. 1.9, е). При значительных деформациях с небольшими скоростями по краям свариваемого контакта появляются напряжения о, обратного знака, разрывающие металл (рис. 1.9, ж).
При стыковой сварке двух стержней (рис. 1.9, ж) эпюра действующих давлений на практике оказывается более сложной, чем для целого стержня (рис. 1.9, е). При значительных деформациях с небольшими скоростями по краям свариваемого контакта появляются напряжения о, обратного знака, разрывающие металл (рис. 1.9, ж).
Рассмотренные модели позволяют сделать заключение о том, что в свариваемых контактах только в редких случаях получается равномерное распределение напряжений сжатия. Неравномерность распределения этих напряжений определяется и формой деталей, и механическими свойствами металла при температурах сваривания. Все рекомендуемые в литературе нормы для величин таких напряжений исходят из условий не только равномерного распределения напряжений, но и равенства приложенных напряжений пределу текучести металла.
Теория пластических деформаций показывает, что средние действующие напряжения сжатия, при которых металл течет, определяются равенством
![]() (1.20)
(1.20)
где S — площадь сечения сжимаемой детали; и — периметр сечения; h — высота заготовки (расстояние между зажимными губками).
Для круглых заготовок формула (1.20) принимает вид
![]() сг = сгт (1 - f
сг = сгт (1 - f
О зависимости такого рода уже говорилось при рассмотрении модели, показанной на рис. 1.9, в. В связи с этим формулы полезно сравнить (1.21) и (1.18).
Все приведенные выше формулы, относящиеся к деформационным напряжениям н их концентрациям, справедливы только для статических нагрузок или нагрузок, прикладываемых с малыми скоростями. Для ударных же давлений все общепринятые показатели механических свойств металла недостоверны. При каждом способе сварки давлением деформационные картины в контакте различны. При сварке взрывом момент образования контакта и момент его сваривания по времени неразличимы. Поведение металла в контакте при холодной сварке и трением — это течение металлических слоев под давлением, а не стабильное соприкосновение поверхностей. Для этих способов сварки представления о контакте, принятые в машиностроении, не применимы. Богатый
теоретический и экспериментальный материал, накопленный в технологии машиностроения, может быть использован для приближенных расчетов только при контактной точечной и рельефной сварке.
1.3. Физическая сущность активации свариваемых * контактов
Активация контакта — это процесс преднамеренного повышения энергии в поверхностных слоях или по плоскости контакта, или, плюс к этому, в некотором объеме металла вокруг контакта. Конечная цель активации — создание сварного соединения. Активирование металла может производиться как в микро-, так, „ и в макрообъемах. Энергия активации может быть получена'за счет любого физического процесса, ограничением обычно служит технологическая целесообразность.
Для сваривания энергию, вводимую в контакт, программируют весьма разнообразно. Поскольку программирование энергии — это количественное изменение ее во времени, то можно сравнивать инерционности приложения каждого вида энергии.
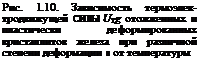
 С этой точки зрения механическая энергия, вводимая в свариваемый контакт для его активации, весьма универсальна и безынерционна по сравнению с энергией тепловой. Если иметь в виду электрическую природу строения вещества вообще и металла в частности, то можно говорить, что всякая активация контакта — это активация внутренней электрической структуры металла. На первый взгляд поэтому кажется, что механическая энергия, по закону термодинамики, способна непосредственно превращаться только в энергию тепловую. И как будто бы только сама электрическая энергия способна электрически активировать металл. В действительности это не так. Механическая энергия — это отличный активатор внутренних электрических процессов в свариваемом контакте в частности, а в металле — и вообще во всем объеме.
С этой точки зрения механическая энергия, вводимая в свариваемый контакт для его активации, весьма универсальна и безынерционна по сравнению с энергией тепловой. Если иметь в виду электрическую природу строения вещества вообще и металла в частности, то можно говорить, что всякая активация контакта — это активация внутренней электрической структуры металла. На первый взгляд поэтому кажется, что механическая энергия, по закону термодинамики, способна непосредственно превращаться только в энергию тепловую. И как будто бы только сама электрическая энергия способна электрически активировать металл. В действительности это не так. Механическая энергия — это отличный активатор внутренних электрических процессов в свариваемом контакте в частности, а в металле — и вообще во всем объеме.
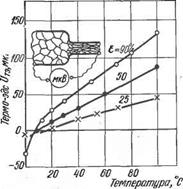
На рис. 1.10 дана экспериментальная кривая, показывающая термоэлектродвижущую силу UT3 отожженных и деформированных кристаллитов железа, измеренную через длительный промежуток времени после деформации. Такая стабилизированная картина устанавливается через несколько минут с момента деформации. В начальный же момент значение этой термо-э. д. е. превышает стабили -
зированноє в 10—15 раз. Такое или даже большее превышение определяется скоростью деформации, которая может обеспечить и весьма ощутимое повышение температуры зоны контакта. Таким образом, механическая активация свариваемого контакта обеспечивает в нем не только развитие теплового, очень привычного нам эффекта, но и одновременно создает явно электрические процессы. Однако сварщики не должны пренебрегать элек- тротепловыми эффектами в свариваемых соединениях. Их признание весьма заметно поможет более глубоко и достоверно понимать физическую сущность металлического контактирования вообще. Каждый процесс сварки давлением завершается операцией сдавливания — операцией осадки. Все процессы сварки давлением отличаются друг от друга временной программой операций осадки. Эти операции могут быть:
1) длительно действующими при постоянном давлении; это соответствует процессу диффузионной сварки;
2) ударно-импульсными — характерными для сварки взрывом и магнитно-импульсной сварки;
3) специально программированными, т. е. переменными по силе сдавливания и времени действия этой силы. К этой области относятся, по сути дела, все процессы сварки давлением, имеющие наибольшее применение в современной технике: контактная, холодная, трением, ультразвуковая и даже диффузионная. Ультразвуковая представляет собой способ сварки с наиболее сложной временной программой приложения давления, сочетая ударноимпульсное действие с переменной во времени силой удара.
Каждый процесс сварки давлением может обеспечить высокие качества соединения при соблюдении только двух обязательных условий.
I условие: или все оксидные и адсорбционные наслоения в плоскости свариваемого контакта в процессе плавления контакта растворяются в расплаве;
II у с л о в и е: или все оксидные и адсорбционные наслоения полностью выдавливаются из плоскости свариваемого контакта при операции осадки.
Вакуумирование свариваемого контакта, даже весьма высокое, не может полностью освободить поверхность металла от оксидных и адсорбционных загрязнений.
Условие I полностью соблюдается при контактной точечной и шовной сварке; условие II выполняется для всех остальных процессов сварки: контактной стыковой, трением, холодной, ультразвуковой.
Особый характер имеет очистка плоскости свариваемого контакта при сварке взрывом. При ней свариваемые поверхности очищаются воздушно-плазменной кумулятивной струей.
Как видно из изложенного выше, для основных процессов сварки — контактной стыковой, трением, холодной и ультразвуковой — представляется весьма существенным выяснить физиче - 24
скую сущность операции сдавливания как главной операции* завершающей формирование сварного соединения. При этом в первую очередь следует подчеркнуть, что сваривание может свершиться только в результате пластической деформации и уж никак не упругой. На основании этого можно утверждать: в зависимости от величины сдавливающей силы и от программы ее действия в плоскости контакта могут происходить процессы межкристаллического разрыва; межкристаллического сдвига; всестороннего сжатия кристаллов. Эти процессы могут происходить в любой комбинации друг с другом, каждый по отдельности и даже все вместе взятые одновременно в любом соотношении.
 Для того чтобы хотя бы весьма приближенно оценить количественно межкристаллические пластические деформации, рассмотрим некоторые достоверные модели. Постараемся при этом возможно более строго разграничивать понятия масштабов. В частности, если вести речь о действиях в масштабе элементарных кристаллов, то уже не делать попытки использовать для них константы, известные для макроскопических объемов металла. Это касается не только физических, электрических, механических, но и других констант. Это, к сожалению, касается даже целых понятий, таких, например, как «температура».
Для того чтобы хотя бы весьма приближенно оценить количественно межкристаллические пластические деформации, рассмотрим некоторые достоверные модели. Постараемся при этом возможно более строго разграничивать понятия масштабов. В частности, если вести речь о действиях в масштабе элементарных кристаллов, то уже не делать попытки использовать для них константы, известные для макроскопических объемов металла. Это касается не только физических, электрических, механических, но и других констант. Это, к сожалению, касается даже целых понятий, таких, например, как «температура».
Физически точное определение этого понятия формулируется так: температура — это мера энергии массы движущихся частиц. При этом, вообще говоря, безразлично, о каком движении идет речь — поступательном или колебательном относительно точки равновесного состояния.
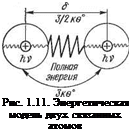
Как видно, понятия «температура» и «энергия» неразделимы. Они и в самом деле неразделимы, даже и в микрообъемах. Допустим, у нас речь идет всего о двух связанных друг с другом атомах кристаллической решетки. Эту модель можно представить в виде схемы, приведенной на рис. 1.11. Собственные гармонические колебания атома относительно точки равновесия — это энергия потенциальная, равная
Еяо, = hvt (1.22)
где h — постоянная Планка, равная 6,62.10-м Дж. с; v — частота колебаний.
Кинетическая энергия атома в целом
Еяяя = &Є, (1.23)
где k — постоянная Больцмана; 6 — абсолютная температура пространства, в котором расположены атомы или, точнее, это тот самый показатель, который определяет кинетическую энергию
одной частицы и который для и частиц привыкли назБівать температурой.
 Полная энергия системы равна сумме кинетической и потенциальной энергии при трех степенях свободы
Полная энергия системы равна сумме кинетической и потенциальной энергии при трех степенях свободы
Е — Епот 4* Еивн ™ 3kQt (1.24)
поскольку Ejiqvj. = Ехи]ц.
Модель, показанная на рис. 1.11, для условий холодного металла представляет собой равновесную систему со стабильным расстоянием между центрами шаровых моделей атомов. Это параметр кристаллической решетки б. Что будет происходить при изменениях этого расстояния, можно выяснить исходя из следующих соображений.
По образной терминологии Я. И. Френкеля, в холодном металле атом находится в состоянии «оседлой» жизни. Если же сообщить ему импульс тепловой энергии, характерный для плавления кристалла, то атом способен мгновенно (снова по образной терминологии Я. И. Френкеля) «совершить прыжок» в соседнюю вакансию, проделав тем самым путь, равный параметру решетки 6. Но ведь можно, следовательно, рассуждать и обратным путем: если мы смогли какой-то силой переместить атом из его стабильного положения на такое расстояние б, значит обязательно тем самым сообщили кристаллу энергию, эквивалентную энергии плавления. А эта энергия совсем необязательно должна быть тепловой, она может быть и электрической, и, что самое интересное, — механической.
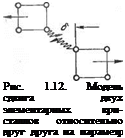
«Прыжок» атома в соседнюю вакансию совершается, разумеется, уже не с той «холодной» частотой, с какой он пребывал в состоянии равновесия, а с той мгновенно высокой, какая характерна для частоты плавления. Но как только атом «оседлает» вакансию, он мгновенно отдает избыточный импульс колебательной энергии в пространство, т. е. соседним атомам, и система успокаивается, снова на низкой частоте холодного металла. Таким образом, если сдвинуть (рис. 1.12) один целый кристалл относительно другого на единичный параметр б, то эта операция будет эквивалентна энергии плавления, но в объеме, занимаемом только этими двумя кристаллами. Все остальные кристаллические «соседи» вокруг этих двух сдвинутых почувствовали этот сдвиг только как факт звуковой затухающей волны. В этом и заключается особенность высокоэнергетического процесса в микромасштабе: механической силой был создан элементарный сдвиг, не разрушивший целостность кристаллической связи и совершенно не замеченный большой массой металла. Тем не менее мгновенная энергетическая вспышка в двух элементарных кристаллах эквивалентна акту их плавления. Эту формулировку полезно запомнить для дальнейшего понимания операции осадочного давления при сварке давлением.
С изменением межатомного расстояния б связаны еще и следующие процессы. Так, в частности, известно, что при всестороннем сжатии кристалла, когда удается уменьшить его параметр только на одну четверть, на такой эффект затрачивается энергия, равная энергии плавления. С учетом этого на рис. 1.13 построена кривая изменения энергии кристалла в зависимости от изменения расстояния между его частицами. Точка 1 соответствует энергии холодного металла, для которого и измерены расстояния 6. Сдвиг атома до точки 2 создает разрыв связи и это соответствует энергии плавления Еал. Вся правая часть энергетической кривой от точки 1 показывает изменение энергии кристалла при деформациях сдвига. При этом, если сдвиг от точки 1 до точки 2 дает. атомный прыжок в соседнюю вакансию, и это является случаем пластической деформации, то движение атома от точки 1 к 4 обратимо и характерно для упругих деформаций. То же происходит и при сжатии, когда атом смещается в точку 3 и также с увеличением энергии. Разумеется, не следует забывать, что деформации кристалла— это одновременно и деформация внешних орбит свободных электронов. Схематически такую деформационную картину можно представить с помощью рис. 1.14, на котором изображена энергетическая кривая свободных электронов.
Расстояние г0 соответствует размеру электронной оболочки невозбужденного атома, т. е. не подверженного пока никакой активации. Но вот кристалл подвергнут растяжению силой F. Здесь прежде всего следует отметить существенную разницу между параметром решетки б и расстоянием г0. Связь друг е другом частиц кристаллической решетки иногда справедливо моделируют в виде
Рис. 1.14. Схема изменения энергии электрона в зависимости от деформации электронной орбиты (с) и схема концентрации электрических и мехннческих сил дефекта (б)
пружин, которые при отклонении от своего равновесного состояния сопротивляются и сжатию, и растяжению, возвращаясь в исходное состояние, если деформации были в пределах упругости, и разламываясь, разрываясь, если деформации были пластическими.
Никаких разрывов электронных конфигураций не наблюдается. Эти конфигурации подвижны и непрерывно обеспечивают или мгновенные, или даже длительные равновесные электрические состояния всех зон деформируемого металла. Электроны в атомах при этом непрерывно меняют и свои орбиты, и свои частоты, а каждый переход с одной орбиты на другую сопровождается или поглощением прилагаемой энергии, или ее излучением в пространство.
При любом изменении стабильного радиуса г0 (рис. 1.14, а) на А г электрон или поглощает энергию, или излучает. Электрон может, однако, и уйти далеко от равновесного расстояния г0, если ему передана достаточная энергия. При сообщении ему энергии, равной или большей работы выхода, такие электроны могут в зоне разорванных кристаллов А создать облако отрицательного заряда, компенсирующего положительный потенциал разъединенных кристаллов.
Рассматривая рис. 1.14, б, можно дать некоторое физическое объяснение явлению концентрации механических напряжений сжатия или растяжения относительно трещины, надреза или даже постороннего включения в исследуемом контакте.
Зона D соответствует ненапряженному участку металла и стабильному радиусу максимума электронной конфигурации свободных электронов г0. Зоны В и С — зоны упругих напряжений, зона А — это разрыв металлической связи. Если измерять действующие силы связи как действующие локальные напряжения, то в зонах В они особенно велики и не зависят от того, является ли действующая сила растягивающей F или сдавливающей Р. Независимо от знака деформации свободные электроны мгновенно перераспределились и создали временную равновесную электрическую структуру в зонах В и С.
Каждое движение атома — это одновременно и движение связанных с ним свободных электронов, поскольку только такое совместное движение обеспечивает сохранение электрической нейтральности. Но вот представим себе поверхность, которую механически деформируем и нагреваем. Такая поверхность обеспечивает, очевидно, выброс в пространство свободных электронов за счет одновременно и термоэлектронной и экзоэлектронной эмиссий. Значительная убыль свободных электронов в пространство над кристаллом весьма снижает отрицательный потенциал внутри кристалла. Положительно заряженные частицы кристаллической решетки начинают друг друга взаимно отталкивать и выталкивать из кристалла, а если уход массы свободных электронов происходит быстро, то это можеї привести к взрыву кристалла. Если оценить энергетические характеристики этого эффекта, то такого рода разрушение кристалла далеко выходит за пределы понятия плав - 28
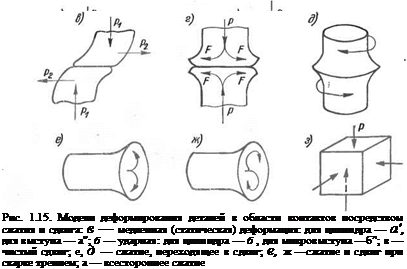
ления. Однако эти процессы «плавления» или даже «кипения» могут быть и не замечены любой термопарой. И не только термопарой. Атомные осколки разрушенных кристаллов мгновенно, вслед за разрушениями, строят новые, обычно дефектные кристаллы. И это происходит по плоскости контакта и иногда в объеме только нескольких кристаллических слоев, что совсем не мешает называть это микродефектное строительство свариванием. Какой бы ни возник по плоскости контакта атомно-электронный беспорядок, он обязательно после прохождения энергетического максимума превратится в металлическую связь, не только не уступающую связи межкристаллитной, но по прочности даже превосходящую ее. Тот факт, что каждый процесс сварки давлением заканчивается плоским сдвигом, становится ясным из рассмотрения Энергетической кривой, показанной на рис. 1.13, и технологических схем, приведенных на рис. 1.15. Деформации растяжения и сдвига (см. правую часть рис. 1.13) идут при значительно меньших затратах энергии, чем всестороннее сжатие. Вполне естественно поэтому, что сила сжатия Р (рис. 1.15) при всех способах сварки давлением обязательно превращается по плоскости свариваемого контакта в силу сдвига F. Это превращение всегда оказывается самым последним эффектом при формировании сварного соединения. Меж - зеренный и межкристаллический сдвиг по плоскости контакта,
![]()
деформация сдвига металла вокруг плоскости контакта ■ • вот чем заканчивается каждый процесс сварки давлением.
Произведем некоторые расчеты. Если на какой-то объем металла действует сила сжатия Р и деформирует этот объем на размер А, то механическая энергия Ph (Дж), по первому закону тер - модинамики, за счет внутреннего трения в металле неизбежно перейдет в энергию тепловую. Это бесспорное положение можно записать в виде
Ph = Ve (deldt) а = ycVT, (1.26)
где V — деформируемый объем; в — относительная деформация; dzjdt — скорость деформации; — коэффициент пропорциональности; ycVT — подъем теплосодержания деформируемого объема.
Поскольку сила Р — pS, то
Как видно по единице физической величины» щ (Дж/с)/ема — это динамическая вязкость или (по другой терминологии) внутреннее трение. Эта характеристика часто используется и ее численные значения определены для многих веществ, в том числе и металлов, но только для жидкого или даже парообразного состояния. Для металлов в твердом состоянии опытных значений коэффициента tj нет. Определим эту характеристику расчетным путем, используя для этой цели принцип механического подобия.
Соотношение (1.25) может быть отнесено к любому как макро-, так и микроскопическому объему. Существуют и механические понятия, которые можно использовать как в отношении макроскопических моделей, так и микроскопических. Например, энергию пружины (Дж) определяем так:
Дпр = Пб2/2, (1.27)
где D — жесткость пружины; б — ее деформация.
Упругопружинными свойствами обладает и любая кристаллическая система. Ее потенциальную энергию (Дж) можно также определить, если вместо константы жесткости D использовать другую константу, которая пригодна для любой кристаллической организации независимо от ее объема. Такой константой, согласно (1.26), является динамическая вязкость. Приравнивая энергии из формул (1.26) н (1.27)
*)S* яа _ D&
2t ° ~ 2 ’
получаем
D = щеЧЦ. (1.28)
Пружинная энергия кристаллов при их деформации и сдвиге превращается в потенциальную
Из равенства формул (1.27) и (1.22), заменяя константу D константой tj, по формуле (1.28) находим
П = 2ftv(/(e263). (1.29)
Если в этой формуле 8 — параметр кристаллической решетки; в — относительная деформация, равная единице при сдвиге на один-параметр решетки б; время t тоже полагать равным единице, то при v (частоте колебаний атомов холодного металла), значение динамической вязкости г] может быть вычислено по табл. 1.2.
В качестве примера можно привести расчет для меди:
![]() 2-6,62.1,5-Ю*3 (108)8-1
2-6,62.1,5-Ю*3 (108)8-1
10ЗЛ (2,55)8
Расчетная формула (1.29) может быть выведена и из других соображений, относящихся непосредственно к деформации сдвига кристаллов.
Если для сдвига кубического кристалла на один параметр решетки необходима сила Р, то энергия сдвига
Рб = р626 = рб3.
Эта энергия превращается в потенциальную fev, т. ©.
Подставляя сюда значение р, получаем
![]() б3 — hv.
б3 — hv.
И, соответственно, динамическая вязкость определяется, как и было записано выше, по формуле (1.29)
т) = 2ftv(/(63sa). (1.30)
Соотношение (1.25) не зависит от величины деформируемого объема, оно определяется по первому закону термодинамики, который действителен и для кристаллических масштабов.
Динамическая вязкость в зависимости от температуры меняется по сложной кривой. Нулевое значение для металлов лежит за пределами точки плавления. Если иметь в виду процессы сварки давлением, для которых температура в плоскости контакта не
|
Таблица 1.2. Физические свойства металлов
|
выходит за границу плавления, то для приближенных расчетов можно положить
Ч « їіо (1 ~ Т/Твя). (1*31)
Сопоставляя это допущение с формулой (1.26), получим
Т = 2усЩЦа&) + UT„„ ' (L32)
В этой формуле константы ус относятся все же к макрообъемам металла. Формула (1.32), как будет показано дальше, дает вполне удовлетворительные результаты расчета во всех случаях, когда речь идет о некоторых объемах металла или о контактных плоскостях, где нагретые слои по толщине много больше, чем размеры элементарных кристаллов. Если же исследуется, например, чисто плоскостной сдвиг, то формулу (1.26) следует переписать с учетом того, что процесс происходит в микрообъемах. Тогда
р — Ц^Ц2і) =» Згел.0, (1.33)
где к — постоянная Больцмана, равная 1,38-10-м Дж/К-атом; л — число атомов в 1 см®; 0 — температура, К.
Соответственно с ощутимой неточностью, вызванной заменой абсолютной температуры на температуру в °С, получим из (1.32^
Гл ~ Ш1-/ЦГ+МТПЛ) * (1'34)
В этой формуле относительная деформация всегда равна единице, поскольку здесь сдвиг меньшим не может быть. Практически формула (1.34) более достоверна, чем (1.32), для деформации пирамидальных выступов шероховатых поверхностей, контактирующих друг с другом. В знак именно такой ориентации формулы (1.34) символу температуры придан индекс А.
Согласно предшествующим теоретическим соображениям, мы приняли, что независимо от используемой энергии эффект сваривания свершается в самый последний момент осадки, в момент максимальной концентрации энергии и за короткий промежуток времени. Формула (1.34) позволяет оценить значение той мгновенной вспышки температуры в плоскости контакта, при которой и формируется сварное соединение по этой плоскости идеально чистых кристаллов. Следовательно, идеальная чистота должна быть на таком же уровне чистоты, как и межкристаллитные границы внутри металла, которые не препятствуют ни размельчению зерен, ни их новому объединению.
Таким образом, всякая операция сдавливання при всех процес ах сварки давлением принципиально делится на два этапа: первый этап — подготовительный — это удаление, выдавливание из зоны свариваемого контакта всех загрязнений; второй — непосредственное сваривание. Если металл не подвергается никакому предварительному подогреву, как это имеет место при холодной
сварке, то подготовительная операция обычно требует выдавливания заметного слоя металла по обе стороны от плоскости контакта.
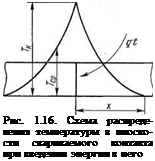 Перейдем к исследованию процессов активации не только плоскости свариваемого контакта, но и некоторого слоя металла вокруг него. Никаких ограничений по видам энергии вводить не будем. Тогда для любого распределения температуры вокруг контакта можно будет написать равенство (рис. 1.16)
Перейдем к исследованию процессов активации не только плоскости свариваемого контакта, но и некоторого слоя металла вокруг него. Никаких ограничений по видам энергии вводить не будем. Тогда для любого распределения температуры вокруг контакта можно будет написать равенство (рис. 1.16)
qt = 2у cSxTcv, (1.35)
где qt — энергия, введенная в контакт, Дж; Тср — среднее значение температуры металла в объеме Sx, °С.
Значение этой температуры зависит от формы температурной кривой, которая по координате и времени определяется различными решениями уравнения теплопроводности Фурье,
дТ _ д[1]Т X д2Т
dt а дх2 ус дх2
Как известно, а — коэффициент температуропроводности, см2/с.
В зависимости от начальных и граничных условий уравнение Фурье дает различные кривые распределения температуры в глубину металла от плоскости контакта. Так, в частности, если вводимая в контакт мощность постоянна (q = const), то уравнение Фурье имеет решение в виде такой сложной функции:
![]() Т(Х, t) =
Т(Х, t) =
qVt
где Ф(|) = е-6г —I [1 — G (g)l.
Параметр функции
£=лг/(2 Yat). (1.36)
Выражение для G
тоже представляет собой одно из решений уравнения Фурье.
Для случая, когда под действием мощности q в плоскости контакта мгновенно вспыхивает температура Тк, распределение температуры вокруг контакта определяется формулой
7W, = Тк [1 — G (1)1,
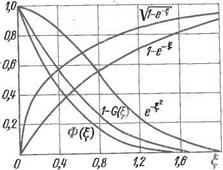
На рис. 1.17 графически представлены эти функции.
2 К - А. Кочергин
Для технологических расчетов достаточны меньшие точности и более простые формулы, сохраняющие наглядность связей всех переменных. Имея это в виду, можно аппроксимировать без больших ошибок кривые рис. 1.17 средней прямой, которая пересечет ось параметра при его значении £ « 1. При этом условии глубина, на которой температура не бу - Рис. 1.17. Графики функций Ф (|), 1 — детповышаться(см. рис. 1.17), G(|), е-52, 1 _ є-*, /П7І определится так:
 х = 2 У at. (1.37)
х = 2 У at. (1.37)
Такую величину для х и можно принять при развертывании формулы (1.35). Тогда среднее значение температуры нагретого металла Тср в зависимости от формы температурной кривой может быть принято таким:
Т’ср — тТк. (1.38)
Для прямолинейного падения температуры m = 1/2, при выпуклости и вогнутости кривых значение m практически не выходит за пределы 7з—2/3.
Учитывая (1.37) и (1.38), перепишем равенство (1.35): qt = TK4mycS У at,
откуда
Эта формула позволяет сделать далеко идущие теоретические и практические выводы. Прежде всего следует еще раз подчеркнуть, что для числителямы не ставили никаких ограничений. Это — энергия, и притом какая угодно: однородная или комбинированная. Следовательно, для случая приложения к контакту только механической энергии формулу (1.39) можно переписать так: если
Эта формула еще раз отчетливо показывает, что в стремлении получить в контакте максимально возможную вспышку темпера - 34
туры Тк, необходимо механическую энергию PhM вводить в плоскость контакта или ударно-импульсным режимом, или кратковременным сдвигом.
Исследуем структуру формулы (1.39) с точки зрения ее критериального содержания. Безразмерное сочетание переменных (1.36) перепишем так:
412 =или ^ = Бо, (1.42)
где Fo — безразмерная критериальная величина at/x2, или критерий Фурье.
Кривые, приведенные на рис. 1.17, показывают, что различные решения уравнения Фурье являются функциями от критериальной величины (1.36), или, что тоже самое, критерия Фурье. Можно показать, что уравнение теплопроводности Фурье построено на этом критерии. Если отбросить знаки дифференциала и разделить обе части равенства на отношение Tjt, то получим определение (1.42).
Некоторые тепловые задачи решаются с помощью уравнения Фурье, учитывающего мощность теплового источника,
где q0 = qlx, Вт/см.
Разделив обе части равенства (1.43) на Tit, получим:
![]()
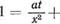
![]() і at і
і at і
ИЛИ 1 = —V + х2
Как видно, здесь фигурирует еще один критерий, который получил имя академика М. В. Кирпичева,
К* ""ТГ = Wx ’ -44)
где q — мощность источника, Вт.
Оба критерия (и Фурье, и Кирпичева) позволяют создать для некоторых процессов сварки расчетные формулы по определению сварочных режимов. Закономерность их применимости может быть доказана следующими выводами.
Из формулы (1.39) получаем
4 пг =---- ут==—р=-.
тк V byes V t
Умножаем числитель и знаменатель на коэффициент теплопроводности А,. Тогда
Этот вывод дает право сформулировать общее заключение: тепловое состояние свариваемого контакта, активированного любым видом энергии, определяется произведением критерия Кирпичева в первой степени на критерий Фурье в половинной.
Вывод (1.45) можно записать такими формулами, вводя обобщенный критерий подобия К:
K = Ki/FS; К= T^vr - 0.46); (1.47)
Вернемся еще раз к формуле (1.39), обратив внимание на то, что для энергии qt мы не ставили никаких ограничений, т. е. она может быть любой: тепловой от экзотермической химической реакции, электрической, механической и пр. Если иметь в виду современные используемые виды энергии, то qt может быть представлено суммой:
qt = фтсд + /2(jRk + /?„) tn - f UItH -[ e(Jn - j- p//2 - j - PhM, (1.48)
где RK и RM — изменяющиеся в процессе нагрева электрические сопротивления контакта и самого металла; ts, — время действия сварочного тока /, т. е. время нагрева.
Из этой суммы энергий технолог может выбирать или любой один вид, или любые комбинации из членов в сумме, если только это может дать желаемый технологический эффект. Первое слагаемое в равенстве (1.48) относится, например, к газовому или термитному нагреву, второе — к контактной сварке, третье — к ней же для процесса оплавления или искрового разряда; elln — это лучевая энергия; р#2 — энергия магнитная и, наконец, PhK — это энергия механическая. Как ни странно на первый взгляд, о последней надо говорить особо. Дело в том, что простейшее понятие PhM как силы, умноженной на путь, в сварочных процессах может быть реализовано разными путями. Сила может быть статической, ударно-импульсной и знакопеременной. Путь может равняться линейной осадке, но может быть и иным. Так, при сварке трением
qt = PTVy + PochM. (1.49)
В этой сумме у — это путь трения, равный
у = п dnt^р/60, (1.50)
где d — средний диаметр стержней; п — частота вращения детали; £гр — время операции трения.
Формула (1.41) получает такой вид:
Т РтрЛ dn 1/~?тр Рос^м _ (151)
Р 4т60 У кус 4т Y^Yc Vtoe ’
где /?тр — давление при операции трения; рос — осадочное давление по окончании нагрева, которое, как видно, нужно прикладывать за короткое время toc, чтобы, во-первых, не упустить состоя - 36
ния подогрева, достигнутое за время tTp, и, во-вторых, осуществить кратковременный, окончательный, сваривающий сдвиг.
Энергия может быть и комбинированной — электрическая плюс механическая. Их соотношение также может быть разнообразным. Например, для стыковой сварки методом сопротивления
Qt = 1% (Як + Ям) + Я ос^м. (1 -52)
Для стыковой сварки методом оплавления и ударно-стыковой
qt = ^опЯш^оп “Ь Яос/ім, (1.53)
где іоп — время процесса оплавления при действующем токе оплавления /оп и напряжении на свариваемых деталях Uon.
Имея в виду все изложенные выше частные соображения о видах энергии, которые можно вводить в контакт, и о величине температуры в плоскости контакта, которая развивается за счет этих энергий, следует написать:
ТСВ = ТК + ТА. (1.54)
Здесь первое слагаемое определяется формулой (1.39), а второе — ранее исследованной формулой (1.34). Если полностью развернуть сумму (1.54) по всем возможным составляющим вводимой энергии, то получим общее энергетическое равенство для любых процессов сварки
т = I2 VTn (Rk ~Ь Ям) I UОП^ОП У ^ОП і св 4m У XycS 4m УXycS
![]() _j______________ УОС“М______ |_
_j______________ УОС“М______ |_
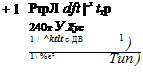 |
|
4m У Хус У toc
Равенство (1.55) интересно тем, что оно показывает, как можно комбинировать виды энергии для известных и освоенных процессов сварки. Например, стыковую сварку методом сопротивления определяют только два слагаемых равенства (1.55) — это первое и третье; для сварки непрерывным оплавлением — второе и третье; для сварки оплавлением с подогревом — первое, второе и третье. Однако это чисто внешние технологические признаки. Вскрыть внутреннюю сущность, а точнее, определить вклад каждого из слагаемых равенства (1.55) может только численный расчет. Для некоторых способов сварки, как, например, контактной точечной и шовной, можно и без расчета определить, что для них используется только первое слагаемое, поскольку металл доводится до плавления и поэтому осадочное давление не нужно. В этих процессах давление обеспечивает другие функции: оно создает начальный холодный контакт и во многих теперь случаях осуществляет опера-
цию проковки уже сваренного горячего металла. Равенство (1.55) может быть продолжено, например, для ультразвуковой сварки
qt=Pbut, (1-56)
где Р — сила сжатия; 1 — амплитуда колебаний; to — частота колебаний; t — время полного цикла.
Соответственно (1.56) в сумме (1.55) появится слагаемое
Р**/И( 4 т |/hус).
Равенство (1.48) еще более существенно и в другом. Оно позволяет предсказать возможность создания новых, пока не используемых процессов сварки. Вряд ли, например, можно отрицать, что когда-нибудь не окажется целесообразным использовать одновременно и энергию трения, и электрический нагрев, т. е. суммировать первое и четвертое слагаемые. Могут быть и другие комбинации, например, любого из электрических нагревов с колебаниями ультра-, гипер - или просто звуковыми. Последние, например, С. И. Кучук-Яценко уже сочетает со вторым и третьим слагаемыми равенства (1.48).
Единственно, какой Процесе сварки давлением не вписывается в равенство (1.48), так это диффузионная сварка в вакууме. Для нее, в классическом ее виде, при постоянных температуре и давлении в этом равенстве не подходит ни одно слагаемое.
Коэффициент диффузии, согласно определению Я - И. Френкеля, для условий печного нагрева
D = Ш(т]б), (1.57)
где kQ — тепловая энергия, которая сосредоточена в свариваемых деталях; при диффузионной сварке она равномерно распределена как по зоне контакта, так и по всей детали в целом; ті — динамическая вязкость, или внутреннее трение; б — параметр кристаллической решетки.
В последние годы для диффузионной сварки стали использовать программированное ударное давление. Мало того, замечено, что внешнее магнитное поле тоже оказывает влияние на процесс диффузии. На основании этих фактов формулу Я. И. Френкеля (1.57) следует дополнить механической ударной энергией фононов hv и магнитной р#2. При этих условиях коэффициент диффузии можно определить по такой формуле
D = (£0 + hv + (л//2)/(т]б). (1.58)
В знаменателе этой формулы коэффициент, характеризующий внутреннее трение, как и ранее, определяется формулой (1.31).
Формула (1.58) показывает, что коэффициент диффузии по свариваемому контакту может возрасти действительно в миллионы или даже миллиарды раз против его значения, известного для условий статического нагрева всего объема металла. Такие именно миллионнократные возрастания за счет ударных давлений и были 38
зафиксированы экспериментально Л. Н. Лариковым, В. Р. Рябовым и В. М. Фальченко.
Формула (1.58) дает объяснение совершенно необычной скорости диффузии при сварке взрывом. В момент соударения зафиксированы частоты более жесткого излучения, чем ультрафиолет. Следовательно, это частоты порядков 1015— 101в Гц. Температура свариваемых поверхностей в результате значительно превышает точки кипения. Внутреннее трение Г] стремится к нулевому значению. Соответственно всем этим фактам коэффициент диффузии D возрастает при сварке взрывом в миллиарды раз по сравнению с тем значением, которое характерно для статических печных нагревов.
Энергетическое равенство (1.48) хотя и содержит много переменных, но не все те, какие вообще участвуют в процессе формирования сварного соединения.
Обратимся к некоторым типовым примерам из практики.
Рассмотрим стыковую сварку методом сопротивления стержней из стали СтЗ диаметром 12 мм. Осциллограмма зафиксировала: среднее значение тока нагрева I = 6350 А. Время нагрева 2,3 с. Сила сжатия Р = 5650 Н. Время осадочной операции toc = 1 с. Размер осадки h = 5 мм. Коэффициент аккумуляции теплоты для стали СтЗ примем -fкус = 1,47 Дж/(см2-°С-с1/2), коэффициент т = 1/2. Тогда при Ph = 5650-5-1(Г8 = 28,52 Дж
Тепловой расчет показывает, что электронагрев в зависимости от величины контактного сопротивления обеспечивает температуру в плоскости контакта 1200—1300 °С. При этих условиях встает парадоксальный вопрос: зачем же вообще нужна механическая осадка, если она добавляет к электронагреву в 1200—1300 °С всего 8,5 °С. Однако выше обращалось внимание на то, что осевая осадка неизбежно завершается сдвиговым эффектом по плоскости контакта. И если на этот сдвиговый эффект положить те же /сдв = = 1 с, то по формуле (1.34) получим
т_________________ I_______________ OOQ °С
д — 6-1,38-0,84-1/1836 + 1/1450 '
А это уже такая существенная добавка, которая или весьма приблизит суммарную температуру Тсв = Ти + Гд к точке плавления, или даже превысит ее, стоит только слегка ускорить операцию осадки. Превышение точки плавления по плоскости контакта не только реальная вещь, но, вероятно, даже желательная. Не следует только забывать, что добавление температуры Тд имеет место только в самой плоскости сдвига, а не в глубинных слоях металла вокруг контакта.
Можно привести и другой характерный пример. Это ударностыковая сварка с разрядом конденсатора на свариваемый контакт. Одна из осциллограмм зафиксировала длительность процесса сварки медных проволок 0,003 с. Время осадки и, следовательно, время деформации сдвига toc = 0,001 с. По формуле (1.34) для меди
Та = 6-1,38-0,85-0,001/1200-1 + 1/1083 = 1076 С-
Отсюда приходится делать вывод, что ударное давление выбивает из контакта весь кипящий металл, нагретый разрядом конденсатора. Сдвиговый же удар по плоскости контакта обеспечивает температуру плавления. Этот факт вполне объясняет структуру сваренного контакта. Его плоскость раздела не отличается от меж - кристаллитных границ. Таким образом, медленная (за 1 с) осадочная операция при сварке методом сопротивления не дает заметной температурной добавки, но скоростная осадка обеспечивает решающий температурный эффект по плоскости контакта. Достаточно заметная по величине составляющая ТА получается и при сварке трением.
На основании приведенных конкретных примеров равенство (1.55) можно расценить как основное технологическое. В нем несколько слагаемых, обусловленных разными видами энергии, но все эти слагаемые дают общую, уже не разделяемую сумму температур. Это значит, что все виды энергии можно регулировать с любой точностью, причем особенно гибко регулируется энергия механическая. В связи с этим следует сделать вывод, что проектировщики современных машин для сварки контактной, трением, холодной мало интересуются скоростью действия сил сжатия, а в основном только их величиной. Характерно, что до сих пор ни в одном литературном источнике не приводится данных о том, какая именно скорость деформации может и должна быть обеспечена. Даются только предельные значения давлений, которые может развить машина. Энергетическое равенство (1.55) убедительно показывает полную недостаточность существующих технологических рекомендаций по параметрам давления. К тому же эти рекомендации неопределенны, поскольку не говорят о программе приложения рекомендуемых давлений. Вот в этой неопределенности и заложены главные причины нестабильности качества сварных соединений. Все приведенные теоретические материалы убедительно говорят о том, что давление должно выжать из плоскости контакта все загрязнения — это условие необходимости. Условие же достаточности обеспечивает завершающий момент деформации сдвига: формируется сварное соединение. И чем кратковременное осуществляется сам сдвиг, тем стабильнее и выше прочность сварного соединения.
Энергетическое равенство (1.48) говорит о том, что любые, до сих пор отработанные и общепринятые режимы могут быть пол - 40
ностью отвергнуты. Вместо них с их установившимися в практике нормами сил сжатия, сил токов и времени действия этих переменных для любого металла могут быть найдены пока не рекомендуемые, но еще лучшие характеристики технологических режимов. Рассмотренные выше теоретические и расчетные материалы дают полное основание сделать вывод: главным и решающим фактором, определяющим все процессы сварки давлением, является механическая энергия, которую благодаря малой ее инерционности можно вводить в свариваемый контакт по любой программе.
Правильное понимание этого принципа позволяет пересмотреть устарелые границы рекомендуемых режимов и найти новые сочетания. например, между электронагревом и осадочными давлениями.
Равенство (1.55) позволяет предсказывать появление новых способов сварки давлением. Их многообразие, однако, будет определять не тепловая, в том числе электрическая энергия, а энергия механическая, различным образом программированная. И термин «контактная сварка» получит, вероятно, более широкое содержание.
Не следует также забывать о возможности всестороннего сжатия отдельных кристаллических организаций. Как было показано на рис. 1.13, деформации такого рода могут создать высокую степень активации контакта. Однако для достижения такой цели скорость деформации должна быть весьма высокой, что обеспечивается при ударной силе. Допустим, что ударно-импульсная сила действует на некоторую, уже макромасштабную плоскость. Тогда можно сказать, что удар фононного потока воспринимают все поверхностные атомы этой плоскости. Колебательная энергия атомов может быть доведена до состояния плавления кристалла, что и определится равенством hvnJI = &0ПЛ.
Зная, что для плавления достаточно сблизить атомы на одну четверть параметра решетки (см. рис. 1.13), можно определить
Vim = Ьвпл/h = 0,208- 10иепл.
Скорость удара для плавления шуд = 6vnJ1/4. Значения этих скоростей для некоторых металлов приведены в табл. 1.2. Как известно, такие или несколько менее высокие скорости удара имеют место при сварке взрывом.
Все изложенное выше убедительно говорит о том, что свариваемый контакт только в редких случаях подобен статическому контакту между металлическими поверхностями. Этот вывод может быть подтвержден и еще одним расчетом применительно к контактированию холодных деталей при точечной сварке. Сохраняя принятую выше пирамидальную модель шероховатости, рассмотрим процесс деформации некоторой единичной пирамиды (рис. 1.18). Допустим, электрод точечной машины своим ударом деформирует эту единичную пирамиду так, что ее поверхность за счет сдвига получает нагрев до температуры 7д, а весь смятый объем нагре-
вается до температуры Тср. Тогда энергетический баланс механического удара электродов запишется таким равенством
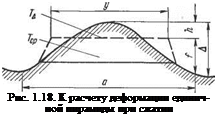 Ph = ycVTcv 4- 2kuTAyt,
Ph = ycVTcv 4- 2kuTAyt,
где V — смятый объем металла пирамиды, V = y*hl3; ycVTcp — теплосодержание объема за счет энергии деформации; кк — коэффициент теплопроводности контакта, совершенно отличающийся от коэффициента теплопроводности металла глубинных слоев.
Значение средней температуры Тср, можно, по-видимому, положить равным TJ2. Тогда энергетический баланс
Ph = ycVTj2 + 2'kvTAyt.
Если коэффициент теплопроводности контакта Як значительно отличается от той же характеристики металла, то следует оценить, в какой мере правомерно'учитывать ус для контакта как характеристику целого металла.
Допустим, что в объеме смятой вершины микропирамиды оказываются запрессованными все оксидные наслоения. Тогда следует сопоставить значения энтальпии ус fДж/(см3• °С) ] металла и его оксидов при Т = 900 °С:
В результате можно сделать вывод, что если смятая железная пирамида будет хотя бы наполовину состоять из оксидов, то и в этом случае величину ус для контакта следует принимать такой же, как и для чистого металла.
Согласно достоверным исследованиям В. М. Попова 116], коэффициент теплопроводности контакта вычисляется по формуле
К = (Ах + Д2)/(2Я),
где Дх и Д2 — высоты контактирующих пирамид; Р — тепловое сопротивление их контакта.
Существуют опытные данные для контакта поверхностей из стали 45, обработанных шлифованием, с высотой пирамиды Дх = = Д2 = 40 мкм. При давлении 58 МПа тепловое сопротивление оказалось равным Р = 1,6-10* (м2-°С)/Вт. Согласно этому,
![]()
![]()
![]() 2А 40-104 25
2А 40-104 25
2R ~ 10е-1,6 ~ 10а
Поскольку коэффициент теплопроводности конструкционной стали составляет 0,4 Вт/(см-°С), то, следовательно, эта же харак - 42
теристика для контакта такой стали в 160 раз меньше. Контакт весьма нетеплопроводен. Для того чтобы определить температуру мгновенного нагрева поверхности пирамидального выступа шероховатости в момент удара по контакту электродами точечной машины, надо решить два уравнения с двумя неизвестными:
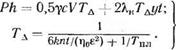 (1.59)
(1.59)
Неизвестными здесь являются Т'д и I.
Рассмотрим конкретный пример точечной сварки стальных листов толщиной 4 + 4 мм. Для них следует предварительно произвести все расчеты, касающиеся вообще площадей контактирования, с использованием формул (1.10), (1.13), (1.15), (1.8).
Вычисления площадей контактирования по этим формулам, как уже отмечалось, справедливы для контактов, которые создаются статическим давлением, и весьма приближенны для условий ударного сдавливания, характерного для точечной сварки. Наименьшая неточность может быть обеспечена в том случае, если выбирать значения предела текучести металла и сопротивления деформации для шероховатостей, соответствующие максимальному наклепу металла. Принимаем следующие значения этих величин. Сила сжатия электродов 8000 Н. Предел текучести стали СтЗ от = 250 МПа. Диаметр сварной точки dT = 12 мм. Контактирующие поверхности обработаны наждачным кругом. Соответственно этому Д = 60 мкм; b — 1; v = 2 (см. табл. 5 приложения). Отношение а! А = 25. Учитывая все это, производим расчеты:
Z = 0,535/d2; Ас = 0,57 см2.
Действующее давление
- р = Р/Ас = 140 МПа.
Основание пирамиды а = 2Д = 0,12 см, тогда
а2 = 144/104 см2.
Число пирамид в границах контурного круга п = Ас/а2 = 40.
По формуле (1.11) критерий X = 0,082.
Здесь принимаем предел текучести, равный 850 МПа, соответственно наклепу, близкому к 90 %.
Фактическая площадь контакта Аг — 0,047 см2. Площадь элементарного контакта смятой пирамиды
у2 .= A fin = 12-10-4 см2; у = 3,42-10"2 см.
Высота смятой пирамиды исходя из постоянства объема определится так:
![]() 2-е
2-е
В данном случае / = 35,35 мкм.
Осадка пирамиды (см. рис. 1.18)
h = А — f = 60 — 35,35 = 24,65 мкм.
Объем смятого участка
V = y2h/3 = 95,5-10-® см3. Относительная деформация
е = 1 — 35,35/60 = 0,41; в2 = 0,168.
Сила сжатия, приходящаяся на единичную пирамиду, р/п = Р' = 8000/40 = 200 Н.
Энергия удара на одну пирамиду ■
P'h = 200-24,5-10-6 = 5- Ю'3 Дж.
Теперь, имея все постоянные величины, напишем для (1.59): 5-Ю-3 = 0,5-5-95,5-10-8Гд + 2-25-10"4-3,42-10-2Гд/;
т’ - ___________ !___________
Л 6-1,38-0,84^/1836-0,168+ 1/1450*
Решая их совместно, получаем:
Гд = 910 °С; t = 0,018 с.
Скорость деформации оказывается около 0,14 см/с.
■ Как видно, и при контактной точечной сварке ударный сдвиг в момент торможения создает мгновенную вспышку высокой температуры деформируемых выступов по плоскости свариваемого контакта.
Все приведенные соображения и расчеты дают основание сделать весьма существенные новые выводы о роли механических деформаций в электрических процессах в свариваемом контакте.
В этой книге неоднократно подчеркивалось отличие свариваемого, весьма динамического в своем поведении контакта, от контакта статического, машиностроительного: скоростное введение механической энергии в свариваемый контакт вызывает в нем одновременно и тепловую, и электрическую активацию.
Основная роль электронных конфигураций в металле проявляется в том, что при всех деформациях, т. е. при любых нарушениях исходной структуры, перемещение электронных конфигураций стремится привести систему в новое, последеформационное 44
равновесие. Равновесие устанавливается не мгновенно, а вспыхивая импульсом, угасает во времени иногда в течение даже не секунд, а минут.'
Степень деформации, ее скорость и геометрия деформируемых микроконтактов различны. В результате между каждой парой выступов получаются различные значения термоэлектродвижущей силы. Эти разности термо-ЭДС создают уравнительные круговые токи по плоскости контакта. Еще большее усложнение вносят оксидные наслоения на металле. Связь металла с его оксидом — чисто электрическая. Всякие разрывы этой связи создают мгновенные электрические микроразряды, которые для тех же микрообъемов вызывают еще один вид активации — электроплазменный.
Вполне достоверно предполагать, что для окисленных поверхностей давление сдвига при ударе создает еще более активированный контакт с образованием в нем одновременно вспышек высокой температуры и плазменной среды. Одновременная и высокотемпературная, и электроплазменная активация является, вероятно, постоянно действующим фактором, определяющим прохождение тока через несзариваемый оксидированный контакт электрод — деталь при точечной сварке. В этом контакте непрерывно чередуются, при каждом ударе, разрывы оксидных пленок и новые их формирования после удара, если толщина пленки не станет столь значительной, что удар не обеспечит ее разрывов.
На основании изложенных выше физических соображений следует признать, что интервал времени между механическим ударом электродов и моментом включения сварочного тока не может быть любым, произвольным.

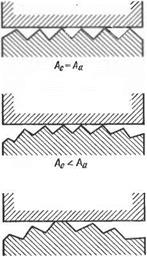

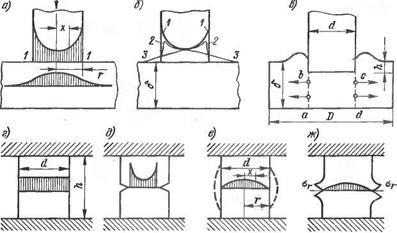
 Опубликовано в
Опубликовано в