Об относительной силе вибрационной связи

между возбудителями

1. О понятии стабильности фазировки при самосинхрониза­ции вибровозбудителей. Устойчивости требуемой фазировки вра­щения роторов вибровозбудителей при их самосинхронизации еще недостаточно для возможности практического использования явления самосинхронизации. Необходимо также, чтобы указан­ная фазировка не была слишком чувствительной к разного рода несовершенствам — к случайному разбросу параметров вибровоз­будителей и двигателей относительно их номинальных значе­ний, вызванному неточностями изготовления и монтажа, а также к влиянию колебаний технологической нагрузки. Если эти не­совершенства приводят к значительному изменению требуемой устойчивой фазировки, то заметно изменяется и характер ко­лебаний рабочего органа машины, что, в свою очередь, может вызвать недопустимое нарушение технологического процесса.

Свойство вибрационного устройства с самосинхронизирующи - мися вибровозбудителями сохранять в заданных допустимых пре­делах рассогласование сдвига фаз вращения роторов возбудите­лей при наличии всякого рода реально влияющих на него факто­ров будем называть стабильностью фазировки такого устройства. Стабильность фазировки представляет собой существенную со­ставную часть общей стабильности рабочего режима колебаний рабочего органа вибрационного устройства [49, 57], а последняя — важную составную часть надежности вибрационной машины — ее способности к выполнению задания в определенном объеме. А именно, можно сказать, что стабильность фазировки есть та составная часть общей надежности вибрационной машины с са - мосинхронизируйяцими вибровозбудителями, которая учитывает специфику применения в ней таких возбудителей.

Стабильность фазировки может быть изучена на основе рас­смотрения основных уравнений, определяющих разность фаз вра­щения вибровозбудителей. Зная возможные отклонения парамет­ров системы, из этих уравнений можно найти отклонения фазо­вых сдвигов Да, от значений этих сдвигов а* — а® в устойчивых синхронных движениях при отсутствии отклонений. При этом в случае малости отклонений параметров и углов Да* основные уравнения могут быть линеаризованы относительно этих отклоне­ний, в результате чего нахождение Да, сведется к решению си­стемы (& — 1) линейных алгебраических уравнений (к — число вибровозбудителей).

2. Случай симметричной схемы с двумя возбудителями. Рас­смотрим сначала вопрос о стабильности фазировки для достаточ­но широко распространенного класса вибрационных устройств с двумя самосинхронизирующимися дебалансными возбудителями, для которых основные уравнения могут быть представлены Б форме

(к»! — со) ± W (со) sin а] = 0,

(9-1)

Р2 == — [/с2 (со2 — со) т W (со) sin а] = 0.

2

Именно так записываются основные уравнения в случае вибро­возбудителей с положительными и не слишком сильно различаю­щимися парциальными скоростями ©і и ©2, работающими в про­стейшей колебательной системе (см. уравнения (6.3) и равенства

(5.16) ), а также в более сложных системах, обладающих некото­рого рода симметрией (см. н. 3 § 10). Через ИЧсо) в уравнениях

(9.1) , как и ранее, обозначен модуль вибрационного момента. Вы­читая уравнения (9.1), получим следующее соотношение для определения сдвига фаз а:

„ VC-2 1

итсюда видно, что при одинаковых парциальных скоростях воз­будителей (©j = ©2) в рассматриваемых системах возможны толь­ко синфазное (а = осо = 0) и противофазное (а = оо = я) враще­ние роторов возбудителей. Поскольку согласно уравнению (8.31)

X = ft> = ± h+Ь. w (to) cos а, (9.3)

то одно из этих движений непременно будет устойчивым, а дру­гое — неустойчивым.

Обозначим через Да отклонение угла сдвига фаз а от его зна­чений ао = 0 или ао = я в устойчивом синхронном движении, имеющем место при одинаковых парциальных скоростях toi и ©г; назовем Да углом рассогласования фаз. Полагая в уравнении

(9.2) а = а<> + Да, получим

|5шДа| = К-Ш1|-^-р~• (9-4)

Вытекающее из (9.2) или (9.3) условие возможности самосинх­ронизации

] W (©) (9.5)

сводится, таким образом, к требованию, чтобы различие между парциальными скоростями вибровозбудителей не было слишком большим. Если обозначить

дш і I Ю2 ~ Ю1 I 1 I К-%)- (Ю1~Юо) I

2 | to |max 2 | to Imax’

РІ = К = 2 kMk, + k2), (9.6)

то из условия (9.5) получим

Ии — Ра/ 9ч> ^ 1> (9*7)

а из формулы (9.4) найдем

J sin Дос |щах == (9.8)

По своему смыслу величины qa и ра представляют собой со­ответственно максимально возможное и максимально допустимое по условию самосинхронизации отклонения парциальных скоро­стей возбудителей от их номинального значения ©о, а величи-

О /

па И(о= ра! Чы может быть названа коэффициентом запаса по са­мосинхронизации. Из формул (9.7) и (9.8) видно, что для обеспе­

чения самосинхронизации необходимо, чтобы коэффициент запаса у. а был больше единицы, а лля обеспечения словия стабильности

фазировки

| Да |Шах <С | ЛоС |тах (9-9)

этот коэффициент должен быть не меньше некоторого минималь­но допустимого значения ив:

Ию хи. (9.10)

Если разброс значений суммарных коэффициентов демпфирова­ния к и &2 не слишком велик (напомним, что возбудители пред­полагаются номинально одинаковыми), то в формуле (9.6) для ко можно принять к = /с2, и тогда получается

k0 = ki — к2. (9.11)

Как показывают расчеты, основными причинами разброса пар­циальных скоростей дебалансных вибровозбудителей являются две следующие.

а) Отклонение скоростей вращения электродвигателей при но­минальной нагрузке, обусловленное неточностями изготовления самих двигателей. Согласно ГОСТ 183-55, п. 30 соответствующее максимальное относительное отклонение для асинхронных двига­телей общего назначения определяется по формул©

„(е) ___ Ле)

— ге) (г)

где пв и п0 —соответственно синхронное и номинальное число оборотов ротора электродвигателя в минуту.

б) Отклонение коэффициентов трения в подшипниках возбу­дителей. Соответствующее относительное отклонение парциаль­ных скоростей вычисляется по формуле [57]

medf 14 со/с* + L ((0)1 = [2 . 'а, (9.13)

о

где те — статический момент дебалансных грузов, d — диаметр внутреннего кольца подшипников возбудителя, / — коэффициент трения в подшипниках, L*>( ю) — номинальный момент на валу

возбудителя, Qf = у | /2 — /і І// — максимальное относительное

отклонение коэффициентов трения в подшипниках; согласно име­ющимся данным qt ~ 0,3. Коэффициенты демпфирования fc0,

и к° и момент L0(6)) могут быть подсчитаны по формулам

к* = ^ "ТГ ' и)" иу к° = }mzda>, к0 = к* + /с°, L0 = п]1(0Р

п„ — п0

С

где і и г] — соответственно передаточное отношение и коэффици­ент полезного действия передачи от вала двигателя к валу возбу­дителя (если, конечно, такая передача имеется; в противном слу­чае г = т] = 1), L(0e) — номинальный момент на валу двигателя.

Имеются и другие причины разброса парциальных угловых скоростей, например неодинаковость статических моментов воз­будителей те величин і и т] и т. п., однако их влияние значи­тельно меньше.

В результате суммарное максимально возможное отклонение парциальных угловых скоростей возбудителей может быть най­дено по формуле

м = /(?»)• +(даТ (9-15>

Эта формула учитывает случайный характер отклонений, вслед­ствие чего одновременное достижение соответствующими откло-

ц ® ® и

пеппямп их максимальных значении и у/ является крайне маловероятным.

Приведенная методика оценки стабильности во многих слу­чаях может быть значительно упрощена. Это упрощение, предло­женное Б. П. Лавровым [164, 166], основано на том очевидном физическом соображении, что стабильность фазировки определя­ется противоборством двух факторов. Стабилизирующим факто­ром является вибрационная связь между роторами, мерой кото­рой, как отмечалось в § 5 и следует также из формул (9.4)—(9.7), может служить модуль вибрационного момента ЙЧсо). Дестаби­лизирующим фактором являются упомянутые выше, как правило, нерегулируемые погрешности изготовления и отклонения техно­логической нагрузки от номинальной [23]). Указанные дестабилизи­рующие факторы в первом приближении можно считать пропор­циональными номинальному моменту двигателя, приведенного к валу вибровозбудителя (если, конечно, двигатель выбран пра­вильно, т. е. достаточной, но не чрезмерной мощности). Тогда мы приходим к следующей величине, которая, так же как и коэф­фициент запаса по синхронизации ии, может служить мерой ста­бильности фазировки самосинхронизирующихся вибровозбудите­лей:

Для стабильности должно выполняться условие

(9.17)

где ка — минимально допустимое значение коэффициента кш, ко­торый назовем коэффициентом вибрационной связи.

Удобство использования величины ка в качестве меры ста­бильности состоит в том, что она содержит легко определяемые величины: момент L0 находится по каталожным данным двигате­ля; легко подсчитывается или оценивается также модуль вибра­ционного момента (см. ниже).

Между введенными мерами стабильности и ка при опреде­ленных условиях существует простая связь. Так, например, если ($)2<(?«)2 и кР^к*, то из приведенных формул получается

= хи Яй 8кы, (9.18)

| sin Да |

так что можно положить иии « 8/сй. Вычисления при несколько иных условиях приводят к зависимостям Ии ~ 5&ш и яв = 5ка.

Заметим, что с коэффициентами хи и ка можно связать веро­ятность наступления эффекта самосинхронизации. Так, если предположить, что величина относительного разброса парциаль­ных угловых скоростей подчиняется нормальному закону с нуле­вым математическим ожиданием и со средним квадратичным от-

1 1 1 I — wi I,

клопсписм стш — - д - дш — - д - | —-— jmax («правило трех сиг­

ма»; см., например, [86]), то согласно (9.6) п (9.7) вероятность

наступления самосинхронизации

(1
U	О)

<Р в

= (41 1 < 30ИХИ) = Ф (Зхв), (9.19)

г

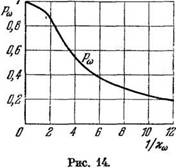
где ф (z) = - Я_ J e~**^dt — интеграл вероятностей. График за - V п о

висимости Р„, от величины 1/ят представлен на рис. 14, при вы­полнении соотношения (9.18) тот же график представляет зависи­мость Ра от величины l/(8fc0), а при иш = 5кы — от величины l/(5fcj.

3. Нормирование и способы повышения стабильности. Разуме­ется, первостепенное практическое значение имеет правильное нормирование минимально допустимых коэффициентов ка и хи

или углов для различных вибрационных устройств; ес­

тественно, что указанные величины должны назначаться больши­ми, например, для классифицирующих устройств, чем для ма­шин, выполняющих лишь транспортные функции. К сожалению, этот вопрос, который должен рассматриваться не только на осно­ве расчетов, но с учетом опыта эксплуатации машин, еще не мо­жет считаться в достаточной мере решенным. Б. П. Лавров рекомендует (см. [466]) для вибраци­онных конвейеров принимать и* не ниже 3,5—5, для вибропитателей в зависимости от их назначения — от 5 до 12 и выше и для грохотов — от 12 до 20. Соответствующие зна­чения будут для конвейеров 0,5—

— 1,0, для питателей 1—2,4, для гро­хотов 1,5—4. Согласно формуле (9.8) этим значениям отвечают значения максимально допустимых углов рас­согласования І Досі шах для конвейе­ров 12—16°, для питателей 5—12°, для грохотов 3—5°. В настоящее время, однако, имеются основания считать, что эти рекомендации явля­ются чрезвычайно осторожными. Так, например, известны случаи успешной эксплуатации вибрационных грохотов с двумя самосинх - ронизирующимися вибровозбудителями, для которых ІДаІшаї®* » 30°, т. е. Ии « 2 и ка « 0,3.

Из формул (9.6)—(9.10) и (9.16) видно, что коэффициент за­паса по самосинхронизации - лы и коэффициент вибрационной свя­зи ка прямо пропорциональны модулю вибрационного момента ТУ (со); формулы, по которым эта величина может быть подсчи­тана для ряда устройств с двумя вибровозбудителями, приводятся в специальной таблице п. 3 § 10; о приближенной оценке Щсо) см. в § 12.

Из сказанного вытекает способ повышения стабильности по­средством увеличения момента TF(co); последнее может быть осу­ществлено как путем изменения параметров (увеличения частоты и амплитуды колебаний устройств и т. п.), так и путем измене­ния структуры системы, например путем увеличения числа сте­пеней свободы несущих тел (см. п. 5).

Другой способ состоит в уменьшении разброса парциальных угловых скоростей вибровозбудителей дю. Это согласно (9.15) и

(9.16) достигается путем выбора двигателей минимально необхо­димой мощности, повышения качества изготовления и сборки под­шипниковых узлов (снижение величины?/), а также путем под-

бора пар двигателей с близкими парциальными скоростями при

номинальной нагрузке (снижение qa)-

4. Об относительной силе вибрационной связи между возбуди­телями. Можно предложить условную градацию относительной силы вибрационной связи между возбудителями в зависимости от значений коэффициентов и кш, представленную в табл. 1.

Таблица 1

Степени относительной силы вибрационной связи Степени отно­сительной си­лы вибраци­онной связи Очень слабая связь Сравнительно слабая связь Сравнительно сильная связь Очень сильная связь Коэффици­ент Хш Коэффици­ 0О. ы<С0,05 0,05<»Св<:0,5 0,5<Xcod ент /сы (при ка — =Яш /5) Вероятность наступле­ 0<&со<0,01 0,01<fcm<0,l 0,l<fcw<0,2 &со >0,2 ния само­синхрони­зации Р и Ра <10% 10%<РШ<50% 50%<Ра<90% Лв>90%

(Эта таблица несколько более детализирована, чем предложен­ная ранее в работе [64].)

В случае очень сильпой связи на возможность самосинхрони­зации и сопутствующих ей явлений можно твердо рассчитывать; в случае сравнительно сильпой связи этого сказать нельзя, но воз­можность таких явлений должна непременно учитываться. При очень слабой связи такие явления, как правило, можно не учиты­вать, а при сравнительно слабой связи — учитывать или не учи­тывать в зависимости от конкретных обстоятельств. Разумеется, что эти рекомендации носят несколько условный характер.

5. Об исследовании стабильности в более сложных случаях. В общем случае вибрационных устройств со многими самосинх - ронизирующимися вибровозбудителями ход исследования ста­бильности сохраняется. В общих чертах он сводится к следую­щему.

а) Иа основе экспериментальных или теоретических данных устанавливаются предельно допустимые по технологическим, прочностным или каким-либо иным соображениям искажения за­кона колебаний рабочего органа вибрационной машины (несу­щего тела или несущей системы тел).

б) Расчетным путем на основе формул типа (8.50) опре­деляется максимальное значение углов рассогласования возбу­дителей | Aas |шах по отношению к номинальной фазировке [24]), при наличии которых искажения колебаний рабочего органа еще ос­таются в допустимых пределах.

в) Значения 1 Aas |тах сопоставляются с теми значениями уг­лов рассогласования 1Да,1тах, определяемыми из основных урав­нений (т. е. уравнений типа (5.І7) и т. п.), которые могут полу­читься при реально возможных неточностях изготовления воз­будителей, их двигателей и т. п.; при этом, как отмечалось в п. 1, основные уравнения обычно могут быть линеаризованы относи­тельно отклонений параметров и углов Aas. Если окажется, что

Аа*|тах <11 Aas |шах, по крайней мере, с достаточно высокой ве­роятностью, то рабочий режим колебаний машины, а также и со­ответствующая фазировка являются достаточно стабильными; в противном случае стабильность следует считать недостаточной и попытаться повысить ее теми же способами, которые были ука­заны выше для случая двух возбудителей.

Более подробно вопрос о стабильности обсуждается в книге [57], в которой, однако, не отражены результаты позднейших ис­следований. В числе таких исследований упомянем о работе О. П. Барзукова, JI. А. Вайсберга, JI. К. Балабатько и А. Д. Учи­теля [91], в которой изучено влияние на стабильность механиче­ской нагрузки, что существенно в случае, когда вес этой нагруз­ки сравним с весом самой машины. Укажем также на статью О. Г. Пирцхалаишвили [231], где рассмотрен способ повышения стабильности путем использования маятниковых подвесок, при­соединяемых к несущему телу посредством упругих шарниров.