Анализ литературных источников показывает, что изложенная теория качественно правильно описывает основные особенности го­рения дуги переменного тока в цепях различных схем.

Для правильного количественного сравнения теории с экспе­риментом необходимо пользоваться экспериментальными данными, ко­торые получены в условиях, где справедливы положенные в основу теории допущения. В литературе соответствующие экспериментальные данные отсутствуют, поэтому воспользуемся результатами проведен­ного авторами исследования дуги переменного тока, горящей в зам­кнутом объеме при большом давлении. Диаметр разрядной камеры был равен 100 мм, эффективное значение силы тока ~ 600 А. Стабилизация положения дуги на оси цилиндрической разрядной камеры осуществ­лялась путем быстрого вращения этой камеры.

Количественное сравнение линейной теории с экспериментальными данными можно проводить двумя способами: а) определить параметр нелинейности по осциллограмме напряжения на дуге, затем рассчитать эффективное значение напряжения (или напряженности поля) и формы кривых напряжения и тока и сравнить с экспериментальными данными; б) произвести прямой расчет параметров дуги и форм кривых на­пряжения и тока по заданным параметрам электрической цепи, гео­метрии дугового канала и свойствам рабочего газа.

Первый способ сравнения основан на том, что для дуги, горящей в цепи заданной схемы, координата амплитуды напряжения явля­ется однозначной функцией параметра Ь (при заданном отношении

Рис. 7.15. Определение параметра не-
линейности по координате амплитуды
напряжения на дуге

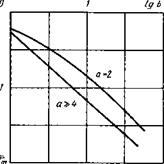а - em/U). На рис. 7.15 приведены

зависимости т (Ь) (где т = 2т /п)

ЇЇІ ш ш

для цепи с дугой и индуктивностью

при а = 2 и а > 4.

Из формулы для Ь (7.8) видно, что при заданных значениях k,

kQ, (j напряженность поля £ является однозначной функцией 6. Отсюда

следует, что если по осциллограмме определить Ь, то можно, во- первых, по формуле (7.7) найти V (или Е) и сравнить с экспери­ментальным значением и, во-вторых, построить теоретические кривые u(t) и Ш) и сравнить их с расчетными.

Необходимо отметить, что при записи через b в формулу (7.7), во-первых, не входят коэффициенты аппроксимации и, что особенно

важно, к ; во-вторых, отношение к /к входит в степени 0,5, что Я Р °

повышает точность определения Е.

Для сравнения с теоретическими результатами используем экспе­риментальные данные, полученные на режиме р = 20 МПа, при этом, согласно оценкам, температура на оси Г = 7000 К. По осциллограмме напряжения находим Ь = 1,2 и по линейной теории рассчитываем «(/). Сравнение этой кривой с осциллограммой (рис. 7.16) показывает почти полное их совпадение. Далее вычисляем k и к при р =

р О

= 20 МПа, Г = 7000 К и по (7.7) находим £ = 110 В/см. В экспери­менте было получено £ = 125 В/см, т. е. расхождение не превышает 1,5 %.

Аналогичные результаты при подобном способе сравнения были по­лучены и при других режимах горения дуги.

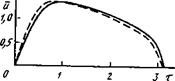Рис. 7.16. Сравнение теоретической и
экспериментальной форм напряжения на
дуге:

--------- эксперимент: .......... теория

Из приведенного сравнения следует, что при определении Ь по экспериментальным данным линейная теория дает правильные качест­венные и количественные результаты, несмотря на то, что для сравнения использовали дугу высокого давления, в тепловом балансе которой важную роль играет излучение, а в линейной теории учет излучения проводится весьма грубо. Этот важный вывод дает осно­вание говорить о применимости линейной теории во многих прак­тически важных случаях, когда температура дуги достаточно высокая, а пик зажигания мал (при большом Ь).

Из этого сравнения также следует, что если по экспериментальным данным определены Е и Ь, то из формулы (7.7) можно найти отношение kp/kg. Поскольку при заданном давлении это отношение является од­нозначной функцией энтальпии (следовательно, и температуры) газа, то по его значению можно определить среднюю за полупериод темпе­ратуру газа на оси дуги.

В разд. 7.6 было показано, что при приближенном учете течения газа в конфузорном канале плазмотрона ’’Звезда” формула (7.7) остается справедливой. Поэтому изложенным выше методом можно оце­нить температуру на оси дуги в конфузорном канале. Для этого по­лагаем напряженность электрического поля в конфузоре постоянной по длине канала и равной полному напряжению, деленному на длину кон - фузора. Подобная оценка проведена на режиме плазмотрона р = 1 МПа,

d =14 мм. При этом Е - 90 В/см, Ь - 230 иТ ~ 14000 К. кр г 0

Рассмотрим второй способ сравнения. Если вычислять Е и b по

формулам (7.7) и (7.8), принимая за г радиус разрядного канала,

д

то получим значения существенно ниже экспериментальных данных, поскольку радиус дуги значительно меньше радиуса канала; однако его реальное значение, которое следует закладывать в расчет, не - известно. Кроме того, в дуге высокого давления очень большую роль играет излучение, точность расчета которого низка. Поэтому прямое сравнение полученных экспериментальных данных с линейной теорией, по-видимому, не оправдано.

Для получения тестовых экспериментальных данных с целью срав­нения с теорией дуги переменного тока А. С. Сергеев разработал специальную установку, в которой воздушная дуга длиной = 500 мм горела при атмосферном давлении в кварцевой трубке внутренним диаметром 24 мм. Последовательно с дугой была включена катушка индуктивности. Один из электродов был сделан подвижным и перед

Рис. 7.17. Сравнение теории с экспе

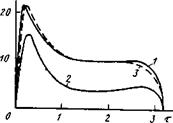риментом:

1 — осциллограмма напряженности эле

ктрического поля; 2 — расчет по не

линейной теории; 3 — расчет по кор

реляционной зависимости

запуском приводился в соприкосновение с неподвижным электродом. После запуска подвижный электрод быстро перемешался под действием пружины и растягивал дугу. В отличие от поджига с помощью зако­рачивающей проволоки такой способ поджига позволял избежать за­грязнения рабочего объема продуктами испарения проволоки. По ос­циллограммам было установлено, что процесс растягивания дуги за­нимал не более 0,1 с, а установившийся режим горения наступал спустя « 0,2 с. Время эксперимента составляло не более 0,5 с. Вследствие присущих дуге переменного тока колебаний мощности и связанных с этим колебаний давления наблюдалось втекание и выте­кание воздуха из трубки. Для исключения влияния движения газа измерение напряженности электрического поля производили в цент­ральной невозмущенной области дуги с помощью двух вольфрамовых зондов,

На этой установке был отработан только один режим по току (/ = = 89 А, т. е. I - І і2 = 125 А). Соответствующая осциллограмма на­пряженности Е(т) приведена на рис. 7.17 (кривая 1). Видно, что пик зажигания существенно больше (ц^ « 2,2), чем дает расчет по ли­нейной теории (и^ = 1,3). Это объясняется относительно малой

температурой газа в дуге, при которой линейная аппроксимация кривой a(h) является весьма грубой.

На этом же рисунке приведена зависимость Е(т), рассчитанная по нелинейной теории при im = 100 A, rQ = 1 см (кривая 2). Видно, что

хотя качественный ход обеих кривых приблизительно одинаков, имеется существенное количественное различие. Анализ показал, что оно обусловлено неучетом излучения, которое в данном случае играет преобладающую роль в тепловом балансе дуги.

Вернемся опять к линейной теории и в соответствии с изложенным в разд. 7.7.2 рассчитаем обобщенное напряжение и 4/ІГ, которое затем перестроим в истинное напряжение на дуге.

Для расчета Ь по формуле (7.8) принимаем 1,5* Ю”4кг(м*с) 1;

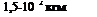Л = 2,5; Г = 0,7; г = 8,5 мм; <о = 314 с ; к

д 0 р

Значение к находим по зависимости объемного излучения воздуха от энтальпии при р = 0,1 МПа, построенной по таблицам работы [1].

_3

Получили ky = 50 кг*м *с. Тогда

2.

k ыг2 Р д

Отсюда видно, что, во-первых, излучение дает основной вклад при расчете значения Ь, и, во-вторых, расчетное значение Ь близко к измеренному по координате пика зажигания на осциллограмме (6 =

= 11). Далее по найденному значению Ь рассчитываем по линейной

теории и иг. а затем с помощью корреляционной функции (см.

рис. 7.12) находим кривую £(т), которая показана на рис. 7.17 штриховой линией (кривая 3). Видно ее хорошее качественное и ко­личественное согласование с осциллограммой.