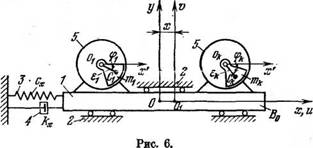
Большинство особенностей постановки и решения задачи о синхронизации механических вибровозбудителей, а также многие закономерности явления, могут быть выяснены на простейшем примере, относящемся к самосинхронизации дебалансных вибро­возбудителей на абсолютно жесткой платформе с одной сте­пенью свободы [31, 57]. Динамическая схема системы изображе­на на рис. 6. Жесткая платформа 1 (несущее тело) может пере­мещаться относительно неподвижного основания 2 в строго

фиксированном направлении Ох. Платформа связана с основани­ем посредством упругих элементов 3 с жесткостью с* и линейного демпфирующего элемента 4 с коэффициентом сопротивления кх. На платформе установлено некоторое число к дебалансных вибро­возбудителей 5 (неуравновешенных роторов), оси которых пер­пендикулярны направлению колебаний платформы и которые приводятся во вращение электродвигателями асинхронного типа.

Описанная система представляет собой частный случай ши­рокого класса механических систем, рассмотренных в § 6 гл. 12 — так называемых орбитальных систем.

Примем за обобщенные координаты системы смещение плат­формы х от положения, соответствующего ненапряженным упру­гим элементам,' и углы поворота роторов ф, (s = 1, ..., к), отсчи­тываемые от направления оси Ох по ходу часовой стрелки. Тогда выражения для кинетической и потенциальной энергии системы запишутся в форме

ft k

Т = jжі* + J-2 + У')' <4Л>

5=1 5=1

к

П = у схх2 + 2 (! — sin ф*). (4.2)

S— 1

Здесь Ж — масса платформы, т, и &ы — соответственно мас­са и момент инерции ротора s-ro вибровозбудителя относительно оси, проходящей через его центр тяжести С., g — ускорение си­лы тяжести, е, — эксцентриситет, а

Zcs = Щ + X + es cos q>s, yCs = v0 — es sin ф3 (4.3)

— координаты центра тяжести s-ro ротора в системе неподвиж­ных осей хОу iuOiv — оси, жестко связанные с платформой и совпадающие с осями хОу при х = 0; и, и v„ — постоянные, пред­ставляющие собой координаты осей вращения роторов о, в осях uOiv).

При учете формул (4.3) выражение для кинетической энер­гии (4.1) преобразуется к виду

к к

Т = j Мх2 + -| 2 ж 2 м&Ч*sin Ч>«- (4.4)

6- Х s—І

Здесь обозначено

ft

м = ж + 2 ms, h = Jcs -Г mfi*. (4.5)

8=1

Составляя теперь уравнения Лагранжа второго рода

d дТ дТ дП р

dt ~

ґде Qj — обобщенные координаты системы, a Qj — соответствую­щие им обобщенные неконсервативные силы, приходим к следу­

ющим дифференциальным уравнениям движения рассматривае­мой системы:

Is<ps = Ls (ер ) — R (ф5) + mses (х sin cps - f g cos q>s)

(* = 1, (4.6)

k

Мх + kxx 4- cx£ = У, m}E:, (cpj sin cpj + rpf cos ф?), (4.7)

j-i

Здесь учтены неконсерватмвные СИЛЫ Qx = —kxZ И Q,=L,{<pa)—

— і?,(ф,), представляющие собой соответственно силу вязкого сопротивления колебаниям платформы ц момент, действующий

на ротор s-ro вибровозбудителя; при этом £,(фв) есть вращающий момент асинхронного электродвигателя (его так называемая ста-

тическая характеристика [13])), а — момент сил сопротивле­

ния вращению, обусловленный, как правило, сопротивлениями в подшипниках; при этом

Rs(<ps) = Rl(<Ps I)Sgnф8, (4.8)

где Rs — модуль момента сопротивления.

Уравнения (4.6) являются уравнениями движения роторов возбудителей, а уравнение (4.7) — уравнением колебаний плат­формы. По своей структуре эти уравнения вполне соответствуют

общим уравнениям задачи о синхронизации динамических объ­ектов (см. уравнения (1.3) гл. 1); в них нетрудно выделить фа­зовые координаты объектов (ср„ и ср„) и системы связи (ж и. г), а также и функции связей.

В делим система (4.G), (4.7) существенно нелинейна. Лишь «ели предположить, тіто роторы возбудителей вращаются равно­мерно, т. е. ф* = os(iDf + aj, где as — постоянные, a lo„l = 1, то уравнение (4.7) превратится в обычное линейноэ уравнение ма­лых колебаний платформы под действием гармонических возму­щающих сил. Это уравнение соответствует предположению, что колебания платформы никак не отражаются на движении возбу­дителей. При изучении ряда вопросов такая упрощенная поста­новка задачи является вполне приемлемой.

При рассмотрении же вопросов синхронизации вибровозбу­дителей нельзя игнорировать наличие связей между колебатель­ными и вращательными координатами системы, ибо как раз наличие этих связей и предопределяет картину движения. Адек­ватные задаче уравнения движения системы при этом, естест­венно, оказываются значительно более сложными. В уравнениях

(4.6) обратное влияние колебаний платформы на движение рото­ров возбудителей отражается слагаемыми те8е, ж sin <р,. Как будет ясно из дальнейшего, именно эти слагаемые предопределяют самосинхронизацию вибровозбудителей, а также другие важные эффекты в рассматриваемой системе.

Основная задача о самосинхронизации вибровозбудителей со­стоит в выяснении условий, при выполнении которых роторы всех возбудителей будут вращаться с одинаковыми по абсолют­ной величине средними угловыми скоростями несмотря на отсут­ствие каких-либо непосредственных связей между ними и на различие параметров, характеризующих возбудители и действую­щие на них моменты. Иными словами, речь идет о выяснении условий существования и устойчивости решений системы (4.6),

(4.7) , имеющих вид

q>s = as [of + as + (tof)] (s = 1, ..., k), x = x (tof), (4.9)

где о — абсолютная величина средней скорости вращения рото­ров, а, — постоянные (начальные фазы вращения), ч]з, и xs — периодические функции времени t с периодом Т = 2л/(й, а каж­дая из величин о, равна либо 1, либо —1; первому случаю отве­чает вращение ротора s-ro возбудителя в положительном, а вто­рому — в отрицательном направлении. Величина синхронной угловой скорости со заранее неизвестна, она подлежит определению в ходе решения задачи.

Движения типа (4.9) в соответствии с терминологией, приня­той в гл. 1, являются простыми синхронными; иногда интерес представляют и кратно-синхронные движения; этот более слож­ный случай, как правило, требует специального рассмотрения (см. [57], а также обзор работ в п. 7 § 8).

Помимо выяснения условий существования и устойчивости синхронных движений, представляет интерес также отыскание, по крайней мере приближенное, закона движения роторов и платформы в устойчивых синхронных движениях, а также реше­ние обратной задачи («задачи синтеза»), состоящей в таком вы­боре параметров системы, при котором обеспечивается существо­вание и устойчивость синхронного движения определенного принтера.

Как показывает опыт и аналитические оценки, в изучаемых синхронных движениях системы вращение роторов мало отлича-

dRs (и) dto

(4.11)

ется от равномерного. Поэтому функции Lsiф,) и /?,(ф3) можно линеаризовать вблизи значения ф, = osg>, положив при учете равенства 14.8) * л • Ls(ф6) = Ls (а6ю) — ks (cps — osa), о • (-4.10) fis (ф«) = osRs (ш) + ks (9S — aso)), где К = - (. , kl d4>s J<Ps=rGs<'> — соответственно коэффициенты электрического и механического демпфирования; оба эти коэффициента обычно положительны, что и будем ниже всегда предполагать. Заметим, впрочем, что окончательный результат получается тем же, если не использовать соотношения (4.10), однако он достигается более сложным путем. Имея в виду решение задачи методом Пуанкаре, введем в систему (4.6) и (4.7) малый параметр р, представив ее в форме h<ps + fcs (ф® — asco) = цФ* (фр, т) (s = 1, ..., к). k. (4.12) Мх + схх = 2 mjEj (ф; sin ф^ - f ф| cos ф^) — yJtxx, і—і где обозначено *) ks = k*s +ks 7 kx = iik’c, (4.13) ііФ. = Т. (a in) — n./i', (o)) ' w. f. (.rsin Такой способ введения малого параметра соответствует допуще- нию о почти равномерном вращении роторов в' разыскиваемом синхронном движении, а также предположению, что рассматри- вается движение вдали от резонанса, когда силу трения кхх в колебательной части системы можно считать малой по сравнению с силой упругости или силой инерции, а также с вынуждающей силой. Впрочем заметим, что в пользу принятого способа введе- ния малого параметра говорят также реальные оценки порядков входящих в уравнепия членов. Подробнее об этом сказало в § 3 гл. XIII, а также в гл. IV книги [57]; там же указано на своего рода «устойчивость» получаемых результатов исследова- ния относительно способа введения малого параметра: эти г»е-

*) Величану ks — k8 -+- ks > 0 назовем суммарным коэффициентом демпфирования.

зультаты, например, изменятся не существенно, если принять также кй — [iks или отказаться от предположения, что кх = ikx - Для решения рассматриваемой задачи можно воспользоваться как непосредственно теоремой § 2 гл. 10, так и результатом ре­шения задачи о синхронизации объектов с почти равномерными вращательными движениями (см. § 4 гл. 12); остановимся на последнем варианте.

Соответствующая уравнениям (4.12) порождающая система

/8фб + к8 (ф" — а[14](й) =0 ($=!,...,&),

к т (4.14)

Мх° + схх° = 2 mJei [фі sin Фі + (фі)2 cos <р®]

і=1

допускает семейство синхронных решений V

2 h

ф,° = Os (at - f as), xn =-------------------- ^—- 2----- COS (cof - f (Xj), (4.15)

to2 — P*

зависящее от к произвольных параметров а,. Основные уравне­ния (см. уравнения (4.6) гл. 12), из которых определяются пара­метры аь..., ah порождающего решения, в данном случае име­ют вид*)

Ps (alt..., aft) s= -^1 <(^ф8 (ф°. *°))> = О

(* = 1, ...,к). (4.16)

Производя усреднение при учете выражений (4.13) и (4.15), а также равенств

сг, = l/as, sin asas = a6 sin as, cosc, as = cosas;

1

<sin (cot - f - as) cos (cot - f as)> = sin (a8 — aj),

<sin (wt + as) sin (at -[- a;)> = <cos (at - f - as) cos (at - j - a,-)> =

= |-cos(as — a,), (4.17)

^уд<?м иметь

<LS (asa) — as/ts (co)> = Ls (asсо) — asRs (со),

<я° sin <р"> =

2т_ j 2 ~ж~ <C0S (wt + sin 03 (wt + =

W Рх j=l

1 gs<0 2 “2 - pI ti

ft

2 ТГ sin ^“s ~ аЛ’ (4-18^

<g cos ф®> = g <cos (of + as)> = 0, в результате чего основные уравнения (4.16) запишутся в форме Ps К, ak) = -^[zs (о., со) - WiK) (a„ ..aft)] = 0

(* = 1 fc). (4.19>

1 "’«є 2 со2 — p.2 -'W

Здесь обозначено WlK) (al7 ..., ah) — — wises <j;° sin ф"> =

Величины Zs и И7!’', имеющие размерность моментов, играют зна­чительную роль в дальнейшем исследовании; назовем их соот­ветственно избыточными моментами возбудителей и вибрацион­ными моментами. Физический смысл этих величин подробно об­суждается в § 5; смьтгл индекса К при W, будет ясен из ска­занного в ц. 2 § 8.

Как и должно быть при решении задачи о внутренней син­хронизации, уравнения (4.19) содержат лишь разности фаз as — ос„ вследствие чего одну из фаз можно считать произволь­ной, например положить ак = 0. Указанные уравнения поэтому содержат лишь к — 1 независимых неизвестных разпостей фаз осі — ак, ..otfc-і — ov, вместе с тем эти уравнения, вообще гово­ря, позволяют определить заранее неизвестное первое приближе­ние к модулю угловой скорости синхронного вращения (О. Для

этой величины из системы (4.19) нетрудно получить одно неза­висимое уравнение, если заметить, что

/ k k

2М — р

, msesrrijEj sin as cos щ —

k h

2 2 msEsrrijEj cos as sin aj = 0 (4.21)

3 3 v_> X j. l

s=X j=l

(тождественность обеих двойных сумм в последнем равенстве становится очевидной, если заменить в одной из них индекс s на /, а / на s). Сложив все уравнения (4.19), предварительно ум­ноженные на ке, при учете (4.21) получим равенство

2 Я. (о., <о) = 0, (4.22)

S—1

или согласно (4.20)'

ft ft

2 osLs (crso>) = 2 К («)• (4.23>

Эти соотношения выражают условие баланса энергии в системе и служат для определения а».

= 0

В соответствии с изложенным в § 4 гл. 12 для существова­ния синхронных движений изучаемого типа необходимо, чтобы уравнения (4.19) допускали вещественное решение относительно разностей фаз a — ak, ..., a. h~ — ah, а уравнение (4.22)—поло­жительные решения относительно а». Каждому такому решению действительно соответствует единственное орбитально асимпто­тически устойчивое синхронное движение, обращающееся при, j. i = 0 в порождающее решение (4.15), если для этого решения arc корни у, алгебраического уравнения Л*-»> степени

д(Рг-рк)	ЧРх-Рк)	8(Pi~Pk)
даг к	да. г	8ak-i
д(Р*-Рк)	4P2~Pk)	°(P,-Pk)
8аг	да2	dcck-i
d(Pk-i~Pk)	д(рь-і~рь)	д(Рп-і-Рн)
да1	да2	dah-1

(4.24)

имеют отрицательные вещественные части. При наличии хотя бы одного корня с положительной вещественной частью соответ­ствующее решение неустойчиво; в случае нулевых или чисто

мнимых корней требуется, вообще говоря, дополнительное иссле­дование.

Заметим, что помимо указанных выше условий устойчивости в рассматриваемой задаче получается еще одно условие, связан­

ное с наличием у характеристического уравнения системы в ва­риациях, отвечающей порождающей системе и порождающему решению, корней р° = е~гкх, равных по модулю единице [31, 573. Однако это дополнительное условие обычно всегда выполня­ется на достаточном удалении от зоны резонанса Я[15] » о и к тому же не зависит от фаз ось..а*.

Поэтому равенства (4.19), (4.22) и (4.24) и являются основ­ными результативными соотношениями теории самосинхрониза­ции вибровозбудителей в рассматриваевом случае.