В предыдущих рубриках приведен алгоритм решения задачи термопластичноети. При этом исходную задачу линеаризовали9 т. е. сводили ее к линейной задаче на каждом шаге прослежива­ния за историей нагружения и на каждой итерации по функции состояния (р и геометрии свариваемого тела. .Рассмотрим теперь численное решение линейной двумерной задачи теории уп­ругости.

В настоящее время при численном решении задачи теории упругости наибольшее распространение получили метод конеч­ных разностей и метод конечных элементов.

Метод конечных разностей уже приводился в подпараграфе 3.7.1 при решении задачи теории теплопроводности. В случав плоской задачи теории упругости, как и в случае температур - ' ной задачи, метод конечных разностей относительно прост, но обладает рядом недостатков, основными из которых являются:

1) трудность аппроксимации криволинейной области прямо­угольной сеткой;

2) равномерность шага сетки, иначе очень усложняется расчетная схема и теряется основное достоинство метода - про­стота. Равномерная сетка исключает возможность учета гео­метрической нелинейности задачи.

Метод конечных элементов лишен этих недостатков, хотя он сложнее и требует более мощной вычислительной техники., В последнее десятилетие численные методы развиваются преиму­щественно на базе конечных элементов. Поэтому при численном решении линейной задачи примем метод конечных элементов, сущ­ность которого изложена в рубрике 3.7.2 при рассмотрении температурной задачи. Несмотря на принципиальное отличие за­дач теории упругости и теории теплопроводности, многие прие­мы реализации метода конечных элементов являются общими, поэтому мы будем часто пользоваться результатами, полученны­ми в 3.7.2.

Из двух вариантов метода конечных элементов - метода сил и метода перемещений - остановимся на последнем, как на более простом и получившем широкое распространение. Идея

х) Более подробно см. [9], главы 3, 5, 12.

метода перемещений заключается в том, что рассматриваемое те­ло разбивается на элементы с узлами в их вершинах и задача решается относительно перемещений узлов, которые однозначно

определяют деформированное и напряженное состояние тела в

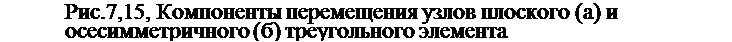
пег—

г

Перемещение является векторной величиной, его представ­ляют в виде двух компонент, которые рассматриваются как ска­лярные величины (рис.7.15), Поскольку это линеаризованная задача, сформулированная в приращениях деформации, то в даль­нейшем будем пользоваться соответствующими приращениями пе­ремещений, Рассмотрим сначала плоскую задачу теории упруго­сти, Распределение горизонтальной йи. х и вертикальной Ли^ компонент приращения перемещений &U в пределах треуголь­ного элемента описывается, как и распределение температуры, уравнением плоскости (см, (3.48)) :

Л u-y = Hi JU)2i+ Nj AUaj + NK AU£k,

где Ni, Nj, NK - функции формы, идентичные представленным в формуле (3.49). Нижние индексы у AU выбраны из условия, что количество узловых перемещений определяется удвоенным количеством узлов. Последние два уравнения можно записать в

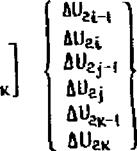матричном виде

260

или

{au.}HX|{AU} , (7.78)

где [N] - матрица функций формы; {йи} - вектор прираще­

ния узловых перемещений.

По известным перемещениям элемента мохно найти его пол­ную деформацию и напряжение. По определению полных деформа­ций в теории упругости

Эи,

Эх

Представляя деформации и перемещения в приращениях, с учетом (7.77) и (ЗЛ9) получим

Эх ~ AU2k_ ,

ДО SftUjg Эйи>^ /р _ дм +1V-AN +

aJxy 0^, + Эх ЄА Чоигн

+ с* AUam+Мия.+ * і йиг j+ К atA&0 і

или в матричной форме

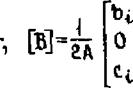Здесь p] - матрица градиентов. Напряжения в элементе [6} определяются по его деформациям {йе.} согласно формуле (7.61) или (7.71).

Таким образом, если известны перемещения узлов всей

системы элементов, то по приведенным формулам можно найти

поле перемещений, деформаций и напряжений. Ножно отметить, что в пределах треугольного элемента деформации и, следова­тельно, напряжения постоянны, как видно из формул (7.80). Хо­тя деформации и терпят разрыв на границах между элементами, перемещения являются непрерывной функцией, тем самым удов­
летворяется критерий сходимости приближенного решения задачи к точному при уменьшении размеров элементов.

Перемещения узлов, как и значения температуры в узлах, определим на основе вариационного принципа. Согласно этому принципу из всех перемещений, удовлетворяющих граничным ус­ловиям, минимальное значение полной потенциальной энергии сообщают те перемещения, которые удовлетворяют уравнениям равновесия. Итак, для определения узловых перемещений следу­ет составить уравнение для потенциальной энергии, выразить ее через узловые перемещения, продифференцировать энергию по каждому узловому перемещению, производные приравнять нулю и полученную систему уравнений решить относительно узловых пе­ремещений. Рассмотрим все этапы этой процедуры достаточно подробно, чтобы можно было довести рассматриваемую задачу до числа,

Полная потенциальная энергия упругой системы П опреде­ляется энергией деформаций в теле Л, и работой, совершаемой внешними силами W :

H=JV-W. (7.82)

Работа V в свою очередь может быть разделена на ра­боту Wp, совершаемую распределенными внешними силами, ра­боту Wt, совершаемую сосредоточенными силами, и работу, совершаемую массовыми силами. При сварке характерны стацио­нарные условия и массовыми силами (силой тяжести) можно

пренебречь. Тогда

n=A~Wp~Wt. (7.83)

Определим все составляющие потенциальной энергии. Из

курса сопротивления материалов для случаев плоского напряжен­ного состояния и плоской деформации известна формула

А- ^ (е] {б} d. V, (7.84)

v. v

где под [z] понимают деформации за весь процесс деформиро­вания. Б рассматриваемой линеаризованной задаче мы поэтапно следим за приращениями деформаций {Ае} и начальными деформа­циями [е°] . Примем 38 начало отсчета энергию на предыдущем этапе нагружения, где удовлетворялись все условия задачи. При - ращение энергии деформации на текущем этапе нагружения опре­деляется аналогично (7.84)

Л*^({АєЬИУ Miv • (7^85)

V

Эта энергия суммируется по всем элементам, С учетом (7.61) и (7.81) получим

yte)

Ф tW'-WT)b,,a№tH£“fl'lv* ‘

е~’ Vte>

ф |г(і»и7мт-итК’]НМ-И)«=

& * у(Й

Ф | |{ійи7[Б1е']Т[Пи][ї<П]Ійи)-[»и)Т[в<‘Тіі>Ю]ІЕ°1-

уф

-№^][в<ег1Н*[e°YP&][е0])<м=Ьі-[йи]т[Б(е>№е>ЮТх

*{il)}AV“ ЩГ[B^]T[Dw]e°}cLV+ [D<fe%°}dvl. (7.86)

yfel y{e1 J

Приращение работы поверхностных сил р, распределен­ных на поверхности тела Ь * определяется следующим образом:

Wp~$(&uxpx+flHyPy')d£=^[fiu}T(p}d5 , (7,87)

s S

где рх і Ру “ компоненты вектора напряжений [р] , парал­лельных координатным осям х, и ^ . Разложим эту работу по

элементам. С учетом (7.78) получим

Wp=£: lfiU}T[N(e)]T|pteHdS. (7.88)

е~' gie> 3

Естественно, вклад в работу Wp может быть только за счет тех элементов, стороны которых образуют поверхность, на­ходящуюся под действием сил р. Приращения работы отдель­ной сосредоточенной силы Р равны произведению этой силы на длину ее пути, т. е.Р(Ш. Поместив в каждой точке приложения

силы узел и обозначив узловые силы через {?} , а узловые

.перемещения через [ни} і работу сосредоточенных сил можно

загшсатъ в виде

wt= • (7.89)

Используя формулы (7.83), (7.86), (7.88) и (7.89), по - лучик уравнение для потенциальной энергии, выраженное через узловые перемещения:

n=g [ Ц М[Л М"-

- j ЬиУТвИ]Т[1)В’]И«+ tle°jT[D<M]it.4d. V-

V® у(е>

A {flu}T[f<(e1]T{pfeljd^-{auT{p} . (7.90)

5(е> ■*

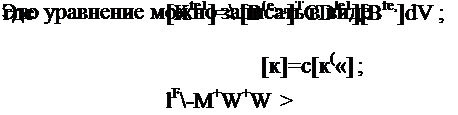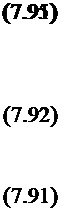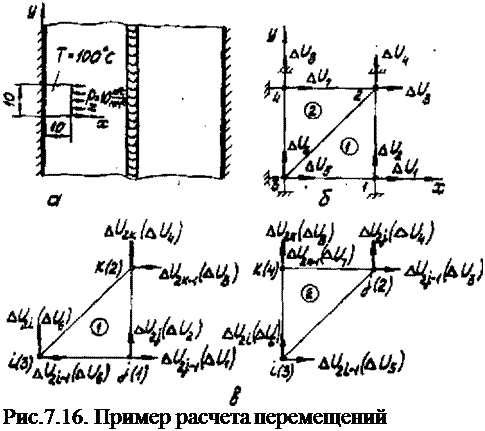
Чтобы минимизировать функционал И s продифференцируем (7.90) по узловым перемещениям [Ли] , пользуясь правилами дифференцирования матричных произведений (3.66), и резуль­тат приравняем нулю:

Видно, что матрица [В] является функцией координат г* и г, поэтому вычисление интегралов, определяющих матрицы

[К**] и ^*0^ , теперь сложнее, так как их нельзя вынести

за знак интеграла. Если элементы относительно малы, то мат­рицы [Ktevl и {*«?} можно определить, приближенно вычис­лив [В] по значениям г и г в центре тяжести сечения элемента, т. е. при г=(гум^+г*уз и 1= (*,L + s - + аЛ)/з. Тогда по формулам (7.94) и (7.96) получим

[к1е'>иГ1т[#’5ет4чЧьи]>ирм]гіг-гй , tow][B(f,№°j4v=[»,a][rfe]t0l гят д.

уф

Черта над [В] указывает на приближенность значения.

В уравнении (7.92) осталось определить вектор {^р*}

Рассмотрим сторону между узлами і и j (см. рис.3.15,б). Опуская промежуточные выкладки, получим
где рг и р*, - компоненты поверхностной нагрузки в на­правлениях гиг. Если поверхностная нагрузка приложена также к сторонам jk или ні элемента, то следует добавить с оотве тствующие елагаемые.

Под внешней узловой силой в осесимметричном случае рг и рй следует понимать совокупность сил, действующих по всей длине окружности, образующей узел элемента.

В отличие от плоской задачи, деформации te и нормаль­ные напряжения огР, , (Гв непостоянны в пределах элемента

и зависят от г и а, как видно из формул (7.103) и (7.73), Принципиальных же различий в алгоритмах решения плоской и осесимметрической линеаризованных задач нет.

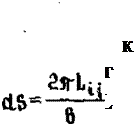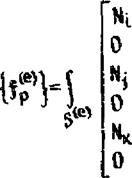Пример.

Последовательность расчета перемеще­ний, деформаций и напряжений просле­дим на простом при­мере. Дана пласти­на толщиной I мм, боковые кромки ко­торой жестко заде­ланы в направлени­ях х. и Nf (рис.7.16,а). Ма­териал ■ пластины однороден, модуль Юнга В — 200 гПа, коэффициент Пуассона ^ = 0,3, коэффициент линейного темпе­ратурного расширения A, = Ю"5 1/°С. Пусть при остывании

после сварки в пластине возникают поперечные растягивающие напряжения рх= 100 МПа (10 кгс/мм2). Выделил у кромки зону площадью 10x10 мм2. Пусть температура этой зоны превышает начальную температуру на 100°С» свойства материала при этом не изменяются. Предположим» что до сварки деформации отсут­ствовали. Требуется определить перемещения, деформации и на­пряжения в выделенной зоне при условии упругого деформирова­ния материала и отсутствия эффекта ползучести.

Разобьем выделенную квадратную зону на два треугольных элемента с четырьмя узлами. так, чтобы разность между номера­ми была минимальной (рис.7.16,б). Пронумеруем в той же по­следовательности узловые перемещения. По условию задачи за­крепим все узлы в направлении у (&Ua= AUj, = AUe=&U8“0 ) и узлы ЗНв направлении х (AUy“M)7=0V В свою очередь пронумеруем в направлении против часовой стрелки узлы и уз­ловые перемещения каждого элемента в отдельности (рис.7.16,в).

Для определения узловых перемещений по уравнению (7.92) необходимо сформировать глобальные матрицы fk] и {F} , для чего предварительно необходимо вычислить матрицы и