На базе решения задачи о напряженно-деформированном со­стоянии балочных конструкций вследствие объемных изменений металла (глава 2) и оценки этих изменений при сварочном на­греве (глава 4) получим расчетные зависимости для определе­ния деформации, напряжений и перемещений в балочных конст­рукциях от продольных и поперечных швов. Под продольными швами в балках будем понимать швы, параллельные ее оси, а под поперечными - швы, расположенные в плоскостях, перпенди­кулярных к оси балки.

§ 5.1. Напряжения, деформации и перемещения в балках от продольных швов

5.I. I. Остаточные деформации и перемещения от продольных швов

Наибольшее практическое значение тлеет расчетное опре­деление остаточных сварочных деформаций и перемещений. В § 4.4 был определен объем продольного укорочения сварного соединения (4.19)

vx= /Ip - *

В это выражение не входят геометрические характеристики се­чения, а коэффициент продольного укорочения jix постоянен при докритических режимах. Поэтому объем продольного укоро­чения до этой формуле может быть определен при сварке полос разной ширины встык к втавр с образованием балки произволь­ного составного сечения. Следовательно, остаточное изменение объема участка произвольной балки единичной длины вследствие наложения продольного шва равно объему продольного укороче­ния сварного соединения, приходящемуся на единицу длины шва. Заменяя в формулах (2.28) на irx, получим

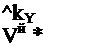где Yt и Zt - координаты оси шва.

Аналогично, заменяя в (2.35) и (2.39) йУтр на йУх,

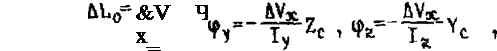получим формулы для определения укорочения длины балки и угла поворота ее концов один относительно другого вследствие наложения продольного вша

где

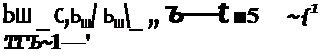Продольный шов при этом может распространяться как на всю длину балки, так и на ее часть. Если шов распространяет­ся на всю. длину балки, то ее ось искривляется по дуге окруж­ности (влиянием концов пренебрегают) и стрелка прогиба посе­редине длины балки определяется по формуле (2*40). Если же шов распространяется на часть длины балки, то искривление оси по дуге окружности охватывает лишь участок шва. Вне это­го участка ось балки остается прямолинейной. В этом случае стрелка прогиба посередине участка балки на длине шва может быть определена также по формуле (2.40), в. которую вместо L, нужно подставить длину участка Ьш. Для оценки стрелки про­гиба всей балки необходимо учитывать поворот на угол. ір пря­молинейны* концов балки. Выражение для стрелки прогиба в данном сечении балки совпадает с выражением для изгибающего момента в том же сечении балки, нагруженной фиктивней на­грузкой, соответствующей кривизне (см. § 2.4). Так, напри­мер, если сварной шов распространяется на длину, охва­тывая среднюю часть балки, то стрелка прогиба посередине ее длины может быть определена по формуле

г ^

где 1^=- - реакция на опоре от фиктивной нагрузки.

В соответствии с (2.42^ деформация в произвольной точке сечения с координатами Y, Z определяется по выражению

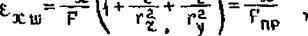(5.4)

где FnP - приведенная площадь сечения (2.44).

Если шов расположен з одной из главннх плоскостей инер­ции. то Yt = 0 ( 1е = 0) и выражения (5.3) и (5.4) соответст­венно упрощаются. В частности, при сварке элементов сдалетр­оичного таврового или двутаврового профиля Yt = 0 и йзгиб возникает только в плоскости стенки. Приведенные формулы мо­гут быть использованы для определения деформаций и переме­щений балочных конструкций, вызываемых продольным прерыви­стым швом. Учет прерывистости шва. производится введением мно­жителя Іщ/t, равного отношению длины участка прерывистого шва 1,ш к его шагу (см. § 4.6). Этот множитель вводится в выражения (5.2) при определении укорочения и углов поворота балки.

Для определения деформаций и перемещений балочных кон­струкций от продольных швов иногда применяют так называемый метод фиктивных сил. Действие продольных пластических дефор­маций укорочения в зоне сварного соединения представляется эквивалентный воздействием некоторой внешней скималцей силы, называемой усадочной, - PVt. Ее величина определяется про­изведением остаточного объема продольного укорочения свар­ного соединения на модуль упругости (ср. с (2.32))

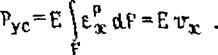
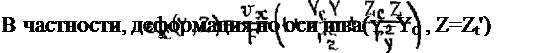(5.5)

По существу, это другая форма представления решения задачи (без принципиального отличия), которая имеет свои преимуще­ства и недостатки.

Преимущества заключаются в том, что расчетные зависимо­сти приобретают структуру, обычную для, формул сопротивления материалов. К недостаткам следует отнести то обстоятельство, что эта форма пригодна только для оценки деформаций, обус­ловленных продольными швами. Применение же объемов укорочения позволяет предложить единую структуру расчетных зависимостей

для оценки деформаций как от продольных, так и от поперечных швов. Кроме того, понятие объема укорочения, по нашему мне­нию, лучше отражает физическую сущность явления и несет' в себе большую информацию, так как характеризует не только ве­личину усилия, обусловленного пластическими деформациями укорочения, но и их распределение.