Исследование влияния локальных неоднородностей на ВАХ ТЭ и ЭХГ требует решения сложной системы нелинейных дифференциальных уравнений, описываю­щих поля температур, давлений реагентов, концентра­ций электролита и поля потенциалов на электродах.

Речь идет о решении сопряженных задач, так как локальная плотность тока зависит от поля температур и потенциалов, которые неразрывно связаны со скоро­стью испарения воды из электролита в поток парогазо­вой смеси, т. е. с полем концентраций в электролите и плотностью паров в парогазовой смеси, и от видов оми­ческих потерь, которые в свою очередь являются завися­щими от распределения плотности тока и поля темпера­тур. Далее надо найти не только эти поля, но и определить некоторые интегральные параметры, харак­теризующие работу ЭХГ в целом и связанные с конст­рукционными и режимными факторами.

По решению поставленной задачи известна лишь одна работа [4.4], в которой разработана программа вычис­лительной машины, определяющая ВАХ ТЭ в зависимо­сти от вышеизложенных неоднородностей. Авторы в про­цессе решения делят поверхность каждого электрода на ряд прямоугольных решеток, каждой из которых при­писывают постоянные по всей поверхности параметры. Предполагается, что ВАХ одного элемента деления явля­ется такой же, как и в небольшом испытуемом ТЭ при некоторых однородных условиях. Информация, касаю­щаяся электродной поляризации, влияния температуры на поляризацию и скорость переноса воды, термические свойства охлаждающего агента, конструкция и удель­ные сопротивления токосъемного тракта вводятся в про­грамму вычислительной машины как входные данные. При этом решается система уравнений, описывающих условия баланса токов и теплового баланса. К недостат­кам работы относится то, что решение проводится для одномерного движения охлаждающего агента и не ясно, как перейти к решению задачи с неодномерным дви­жением. В качестве результатов расчетов приведены поля распределения токов и потенциалов, однако нет обобщающих выводов, дающих конкретные представле­
ния о влиянии тех или иных видов неоднородности на работу ЭХГ в целом.

Для того чтобы определить интегральные параметры, характеризующие работу ЭХГ в целом и связанные с конструктивными и режимными факторами, развитый ранее подход к решению задачи о влиянии омического сопротивления распространим на решение задачи о влия­нии температурного поля на ВАХ ТЭ. В качестве при­мера рассмотрим решение уравнения тепломассообмена для случая, когда съем теплоты с электродов осущест­вляется с помощью протока электролита. Задача решается в предположении, что вся образующаяся в ре­зультате реакции вода испаряется и температура элек­трода практически не отличается от температуры элек­тролита. Кроме того, принимается, что разность потен­циалов на поверхности электродов не меняется, т. е. плотность тока зависит только от температуры. Урав­нение, описывающее изменение температуры электроли­та при его движении, с учетом принятых предположений и уравнения

usVT=Q(T)lWhz,

где П— источник, зависящий от Г; s — направление вдоль линий тока; W — коэффициент, обеспечивающий размерность уравнения, будет иметь вид

Bsvr = ff;(i^)-”-:]^L. (4.23,

где /’—локальная плотность тока; F —число Фарадея» ти0 = 9; U — разность потенциалов между электродами

г) — КПД; г — теплота парообразования; ср— теплоем­кость электролита.

Аппроксимируем зависимость плотности тока от тем­пературы следующим выражением:

/=ЛеМ

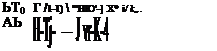где А и b определяются из экспериментальных данных. Проинтегрируем выражение (4.23) с учетом (4.24)

(4.25)

Здесь Т—Т/То, Т0 — температура электролита на входе.

Подставляя выражение для поля температур (4.25) в (4.24) и интегрируя по площади электродов S опре­делим ток:

‘ « • / — J J dS —Л х Д'

. s

Для количественной оценки генерации тока в зависи­мости от неравномерности температурного поля введем коэффициент неравномерности условий токообразования, ' характеризующий в данном случае влияние неравномер­ности поля температур на выходные характеристики ТЭ как отношение полного тока, получаемого в реальном канале, к идеальному /Ид, который может быть реали­зован при той же площади электродов в канале с рав­номерным температурным полем при некоторой опти­мальной температуре,

С учетом (4.26) и (4.27) получим следующую фор­мулу для определения коэффициента неравномерности условий токообразования:

ьт0ль ^ 1—2		"ЧЪОГ ] і г і сра )/	/ Q)

ft 5 X

dS.

(4.28)

Коэффициент fT является функцией геометрической формы канала, отношения компонент тензора проницае.

Мости Yky! kx пористоіГсредьі, расхода и равномерности

раздачи хладоагеита и мощности ТЭ.

Таким образом, анализ решений некоторых упрощен­ных задач о влиянии омического сопротивления и не­равномерности температурного поля на ВАХ ТЭ позво­лил ввести интегральный параметр — коэффициент не­равномерности условий токообразования, благодаря чему стало возможным сравнивать различные конструк­тивные решения, выбирать наиболее оптимальные из них и, внося соответствующие коррективы, повышать выходные параметры ТЭ. Однако все вышеизложенные методы оценки основаны на допущениях одномерности температурных и потенциальных полей и при условии постоянства одного из них. Для более точной оценки влияния неравномерности условий токообразования и возможности строгой и более полной оптимизации кон­струкции и условий эксплуатации ТЭ необходимо найти решение двухмерной задачи, учитывающей одновремен­ное влияние как температурного поля, так и поля потен­циалов.

Для решения этой сложной задачи развивается при­ближенный полуэмпирический метод, основанный на том, что наряду с краевыми условиями в описываемой си­стеме входными данными являются наборы заранее определенных теоретически или экспериментально ло­кальных ВАХ в зависимости от различных параметров— температуры, давления, концентрации и т. д. Для реше­ния поставленных задач используется физическое моде­лирование. При этом могут использоваться не одна, а несколько физических моделей, так что выходные дан­ные одной из них являются входными данными другой. В какой-то мере этот подход отвечает упоминавшейся выше взаимосвязи рассматриваемых явлений и, как по­казывают специальные эксперименты, достаточно близко отражает реальную картину.

Взаимосвязь различных моделей осуществляется сле­дующим образом: предполагая однородным поле потен­циалов на поверхности электродов, можно определить поле температур и парциальных давлений парогазовой смеси, например методом моделирования на гидравличе­ском стенде. Затем, приняв полученное распределение за исходное и зная вид зависимости локальных ВАХ для различных значений этих факторов s=/(0 и s= 188

—/(р) и т. д., можно найти поле потенциалов для урай* нения Пуассона вида

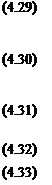
S+7jJ'WC*. и, U)

со следующими граничными условиями:

,, тп и*—и J {х, у, U) — s у)

для области, где генерируется ток, и

4х, У, С/)= О

для области, где не генерируется ток:

?. = *.;

а . ’

— условия на внешней границе рамки в месте присоеди­нения токовыводящих проводов, соединяющих рамку с борнами для катода и анода.

По всему остальному периметру, ’

df — —1 Ox Оу

Для решения данной задачи можно воспользоваться методом комбинированного моделирования, описанным в предыдущем параграфе. Для этого к узловым точкам электрода нужно присоединить переменные сопротивле­ния

У) = к{х7уГв-.......... ' (4>37>

Наиболее наглядно влияние неравномерного темпера­турного поля на ВАХ ТЭ можно проследить при отводе теплоты по периферии электродов. Было исследовано влияние параболического поля температур с разной сте­пенью неравномерности (рис. 4.6) на ВАХ ТЭ. Как вид­но из рисунка, во всех экспериментах вершине парабо-

189

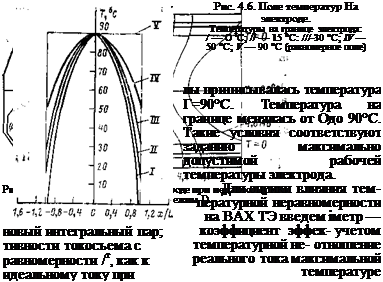электрода, когда омическими потерями можно прене­бречь, при этом напряжение на токосъемниках должно быть одно и то же.

На рис. 4.7 и 4.8 представлены поля потенциалов, полученные на моделирующем устройстве, анализируя которые можно прийти к выводу, что неоднородность исследуемого поля температур не увеличивает, а даже несколько уменьшает неоднородность поля потенциалов 190

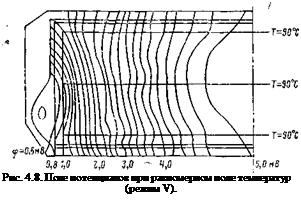
по поверхности электродов. Такое явление можно объяс­нить уменьшением плотности тока на периферийной ча­сти электрода за счет того, что процесс токообразования

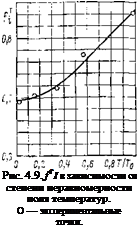происходит при пониженных температурах. Однако, не­смотря на то что поле потенциалов остается почти по­стоянным, коэффициент эф­фективности токосъема с учетом температурной не - равномерности/т,- падает при

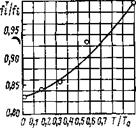
Рис. 4.10. Зависимость вели­чины jTilfi от степени нерав­номерности поля температур. О — экспериментальные точки.

уменьшении Г/То (рис. 4.9). Для равномерного темпе­ратурного поля fTi=fi коэффициент эффективности токо­съема характеризует только омические потери. Отноше­ние этих коэффициентов является мерой ухуд-

шения ВАХ ТЭ за счет неравномерности поля температур для данной конструкции токосъема (рис. 4.10).