Расчет сводится к определению расчетной нагрузки для наиболее нагруженного болта. Затем рассчитывают прочность этого болта по формулам одного из случаев, рассмотренных в § 1.6.

В расчетах, изложенных в настоящем параграфе, приняты следу­ющие допущения: поверхности стыка остаются плоскими (недефор - мируемыми) при всех фазах нагружения, что справедливо только для деталей, обладающих достаточной жесткостью*; поверхности стыка имеют минимум две оси симметрии, а болты расположены симметрично относительно этих осей; все болты соединения оди­наковы и равно затянуты. С некоторым приближением перечислен­ные условия справедливы для большинства конструкций.

Рис. 1.28

Различают три характерных случая расчета соединений, включа­ющих группу болтов.

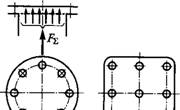
Случай I. Соединение нагружено центральной отрывающей силой, т. е. равнодействующая сила нагрузки соединения перпендикулярна плоскости стыка и проходит через центр тяжести его площади. Этот случай типичен для болтовых соединений круглых и прямоугольных крышек (см. рис. 1.23 и 1.29), нагруженных давлением жидкостей или газов. При этом болтам дают затяжку, обеспечивающую плот­ность соединения. Все болты такого соединения нагружены оди­наково. Внешняя нагрузка, приходящаяся'на один болт,

'"Это допущение позволяет избавиться от сложных расчетов, в которых опре­деляют распределение нагрузки по болтам с учетом деформаций деталей.

F=FjJz,

Где z — число болтов.

Расчетную нагрузку болтов опре­деляют по формулам (1.26), (1.28) или приближенно по формулам (1.36) и (1.37).

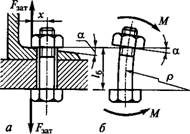
Случай II. Нагрузка соединения сдвигает детали в стыке. Примером служит крепление кронштейна (рис. 1.30). Заданная сила Fz стремится сдвинуть кронштейн вниз по плоскости стыка и повернуть его в направлении часовой стрелки. Полагают, что поворот кронштей­на происходит вокруг оси, проходящей через центр тяжести площади стыка соединяемых деталей. Переместив силу FL в центр тяжести площади стыка и одновременно приложив к кронштейну момент T=FIi19 получают нагрузку, эквивалентную заданной (FПо воз­действию на соединение. При этом сила F^ становится центральной и распределяется по болтам равномерно:

Ff=FZ/Z. (1.38)

Нагрузка от момента (реакции FTl, FTi, ..., FTz) распределяется по болтам пропорционально их деформациям при повороте кронштей­на. В свою очередь, деформации пропорциональны расстояниям болтов от центра тяжести стыка, который является центром пово­рота. Направление реакций болтов перпендикулярно радиусам гь г2, ..., rz. По условию равновесия,

T=FTtr1 + FTlr2 +... +Ft/X9 ^ Где (

> (1.39)

FrJFr^rJri; ...; FTJFT=rJrx. J Для примера на рис. 1.30

Суммарная нагрузка каждого болта равна геометрической сум­ме соответствующих сил Ff И Ft (на рис. 1.30 показана нагрузка для первого болта F{).

Рис. 1.29

Ф ^ Ф

За расчетную принимают наибольшую из суммарных нагрузок. Сравнивая величины и направление реакций, можно отметить, что для соединения, изображенного на рис. 1.30, наиболее нагружен­
ными болтами являются 1-й и 3-й (реакции Ff И Ft близки по направлению) или 2-й (FF и FT направлены одинаково, но FT2<FTi И Ft).

Рис. 1.30

+1 считывают по напряжениям Болты поставлены с за­зором. Нагрузка восприни­

Ь

В конструкции соедине­ния болты могут быть по­ставлены без зазора или с зазором.

Болты поставлены без зазора. Нагрузка восприни­мается непосредственно бол­тами (см. рис. 1.21, б). Про­чность болтов и деталей рас-

Мается силами трения в стыке, для образования которых болтам дают соответствующую затяжку. Приближенно полагают, что рав­нодействующая сил трения, вызванных затяжкой каждого болта, приложена в центре соответствующего отверстия.

(1.40)

Соединение будет прочным (детали не сдвигаются), если равно­действующая сил трения под каждым болтом не меньше, чем соответствующая равнодействующая сил Ff И Ft. Так как по усло­вию задачи болты затягивают одинаково, общую затяжку опреде­ляют по наиболее нагруженному болту (1-му или 2-му; рис. 1.30*). Необходимая затяжка болтов

-^зат ^^maxZ/j

Где К= 1,3...2 — коэффициент запаса; Fmax — сила, приходящаяся на наиболее нагруженный болт, равная, например, F{; F — коэффици­ент трения в стыке деталей[5].

Прочность болтов рассчитывают по формуле (1.19).

Оптимизация конструкции такого соединения может быть выпол­нена за счет: варианта постановки болтов с зазором и без зазора; соотношения размеров а и Ъ расположения болтов; количества болтов. При этом могут быть два случая: размеры кронштейна заданы или подлежат определению. Во втором случае вначале рассчитывают высоту кронштейна по напряжениям изгиба, затем

Рассчитывают соединение и по нему определяют все другие раз­меры.

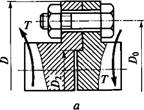
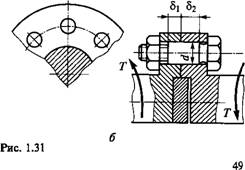
В качестве второго примера расчета группы болтов при сдвига­ющей нагрузке рассмотрим фланцевое соединение валов. В конст­рукции таких соединений обычно предусматривают центрирующие выступы (рис. 1.31, а) или ставят центрирующие шайбы (рис. 1.31, б), которые одновременно разгружают соединение от поперечных нагрузок.

При болтах, поставленных без зазора, расчетная нагрузка болта

F=2T/(ZDQ). (1.41)

При болтах, поставленных с зазором, необходимая сила затяжки

F^lKTKzDoJ). (1.42)

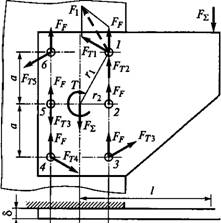
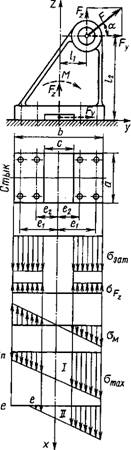
Случай III. Нагрузка соединения раскрывает стык деталей. Этот случай часто встречается в практике (крепление всевозможных крон­штейнов, стоек и т. п.). Метод решения рассмотрим на примере рис. 1.32. Раскладываем силу F на составляющие Fz и Fy. Действие этих составляющих заменяем действием сил Fz и Fy, приложенных в цен­тре тяжести площади стыка, и действием момента

M=Fyl2-Fzlx. (1.43)

Fz и М раскрывают стык, a Fy сдвигает детали. Возможность раскрытия стыка и сдвига деталей устраняют затяжкой болтов

С силой Isai-

Расчет по условию нераскрытия стыка. До приложения нагрузки F затяжка образует в стыке напряжения смятия

^зат = ^зат^Мст, (1-44)

Которые приближенно считаем равномерно распределенными по стыку. В формуле (1.44): Z — число болтов; АСт — площадь стыка.

В этой формуле Fz( 1-х) — доля вне­шней нагрузки, которая идет на разгрузку стыка [см. формулу (1.27)]. На практике в подобных соединениях значение х мало. Упрощая решение, принимаем х=0, что идет в запас по условию нераскрытия стыка.

Сила Fz растягивает болты и уменьша­

Ет (Тзат на

Рис. 1.32

6п

При решении задачи о том, как изме­няются напряжения в стыке под действи­ем момента А/, необходимо выяснить, во­круг какой оси поворачивается кронш­тейн. Применяя принцип наименьшего со­противления, можно полагать, что пово­рот происходит вокруг оси симметрии стыка, так как относительно этой оси воз­никает наименьший момент сопротивле­ния повороту (меньше момент инерции площади стыка). Это условие соблюдает­ся только при достаточно большой за­тяжке болтов, обеспечивающей нераскры­тие стыка. При раскрытии стыка ось по­ворота смещается от оси симметрии к кромке стыка. Если затяжка отсутству­ет, то осью поворота будет кромка стыка. Следовательно, затяжка соединения про­являет себя как пайка или склейка деталей по всему стыку. До тех пор пока стык не раскрылся, кронштейн и основание можно рассматривать как еди­ное целое. Испытания подтверждают это положение.

(1.46)

Рассматривая условия нераскрытия стыка, считаем осью пово­рота ось симметрии стыка (ось х на рис. 1.32). При этом напряже­ния в стыке под действием момента М изменяются в соответствии с эпюрой, аналогичной эпюре напряжений при изгибе. Пренеб­регая значением х-> так же как ПРИ определении о>г, приближенно запишем

(ТмяМ/W^),
где Wn{x) — момент сопротивления изгибу, который определяют для площади стыка.

В зависимости от величин F3&T и F эпюра суммарных напряжений в стыке принимает вид одного из вариантов I или II, показанных на рис. 1.32. Здесь

<W = 0"зат ± 0>z+ 0*f — максимальное напряжение ]

В стыке, К (147)

Ffmin = 0*з&т + GFZ—GM — минимальное напряжение 1 в стыке. *

В этих формулах за положительные приняты напряжения затяж­ки Сзат. Вариант II свидетельствует о раскрытии стыка на участке ее, Так как напряжения здесь равны нулю, что недопустимо. Вариант I иллюстрирует нераскрытие стыка и рассматривается как расчет­ный. Условие нераскрытия стыка,

Ffmin^O,

ИЛИ ИЛИ

(1.48)

Обычно 1,3...2 — коэффициент запаса по нераскрытию стыка.

По условию (1.48) определяют а3&т и затем из формулы (1.44) находят F3ат.

В тех случаях, когда материал основания малопрочен по сравне­нию с материалом болтов, например бетон или дерево, необходимо проверять условие прочности основания по максимальным напря­жениям смятия (см. табл. 1.2):

(1.49)

Если условие (1.49) не удовлетворяется, обычно изменяют размеры стыка.

Расчет по условию отсутствия сдвига деталей в стыке (выпол­няют как проверочный). В соединениях, не имеющих разгрузочного устройства от сдвига деталей, сила Fy уравновешивается силами трения в стыке. Детали не сдвигаются, если сила трения в стыке больше Fy или

[F^z+(-x)Fz}f>KFy, (1.50)

Где /—коэффициент трения в стыке; JRT'«1,3...2— коэффициент запаса по сдвигу.

Ориентировочно можно принимать /«0,3...0,35 — сталь (чугун) по бетону, /«0,25 — сталь (чугун) по дереву;/«0,15...0,20 — сталь по чугуну (по стали).

В формуле (1.50) не учитывается действие момента М, так как момент не сдвигает детали и не изменяет суммарной величины сил трения в стыке.

Если условие (1.50) не выполняется, то это значит, что условие (1.48) нераскрытия стыка не является решающим для данного со­единения и затяжку следует определять по условию (1.50) несдвига - емости деталей

F^=[KFy±(-x)Fim^f) (1.51)

Или ставить болты без зазора.

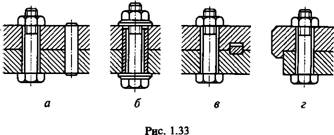
При больших сдвигающих нагрузках применяют также специ­альные разгрузочные устройства (рис. 1.33): штифты (а), втулки (б), Шпонки (в), упоры (г) и т. п. В таких конструкциях болты, постав­ленные с зазором, воспринимают только нагрузки, раскрывающие стык деталей.

При расчете прочности болтов учитывают наибольшую силу затяжки F3АТ из найденных по условию (1.48) или (1.51). Внешняя нагрузка, приходящаяся на один болт от силы FI9

FF=FJZ; (1.52)

Внешняя нагрузка от момента М определяется из равенства

М= I(Fl2el + F22e2+...+№„),

Где I — число болтов в поперечном ряду (на рис. 1.32 I=2); п — Число поперечных рядов с одной стороны от оси поворота (на рис. 1.32 «=2).

Силы Fu F2 пропорциональны их расстояниям от оси поворота: ВД = ^2ит. д.

Учитывая это и заменяя Fi на FM как наибольшую из нагрузок от момента, после несложных преобразований находим

FM=Mem2e + 2el + ...

... + 2ея2)]. (1.53) Суммарная нагрузка

Ь/2

+ +

+ +

+ +

Рис. 1.34

F=FM±FZ. (1.54)

При известных Рж и F расчетную нагрузку определяют по формуле (1.37) и прочность болта по формуле (1.32) или (1.34) с учетом выражений (1.25) и (1.33).

Форма стыка оказывает значительное влияние на прочность соединения. Например, для сплошного 1 и несплошного 2 стыков, изображенных на рис. 1.34, их площади и моменты сопротивления изгибу равны:

Ах = аЬ Ж, = (1/6)д&2; A2=(/2)ab; W^-^ab^

При одинаковой внешней нагрузке М ом во втором стыке воз­растет только на ~ 12% по сравнению с первым стыком, а площадь уменьшится на 50%. При этом условие нераскрытия несплошного стыка можно обеспечить затяжкой болтов, уменьшенной примерно на 38% [см. формулы (1.44), (1.46) и (1.48)].

Комбинированная нагрузка соединения. Рассмотренные три слу­чая расчета группы болтов позволяют производить расчет прочно­сти соединения для любых комбинаций нагрузок. При этом дейст­вие сложной нагрузки расчленяют и приводят к действию суммы составляющих рассмотренных нагрузок.

Оптимизация конструкции соединения здесь выполняется за счет формы стыка. Стык 2 позволяет уменьшить диаметры болтов и площадь кронштейна, необходимую для их размещения. От­метим, что уменьшение площади в два раза, возможно, не являет­ся оптимальным и принято только в качестве примера. Поиск оптимальной формы можно продолжить при других комбина­циях параметров. При этом кроме условия нераскрытия стыка следует учитывать и условие прочности основания формула (1.49), так как с уменьшением площади стыка увеличиваются напряжения смятия.