В большинстве зарядных цепей с активными токоогра­ничительными элементами и вентилями заряд имеет пре­рывистый характер, причем в процессе заряда изменяется не только значение импульсов зарядного тока, но и их длительность, что затрудняет получение точного аналити­ческого решения. Исключение составляет начальный пери­од заряда в схемах трехфазного выпрямления с резистора­ми, включенными на стороне выпрямленного напряжения. Для анализа переходных процессов удобнее всего приме-

к

нять метод усредненных кривых, который заключается в том, что вместо уравнения реальной кривой изменения на­пряжения на конденсаторах отыскивается уравнение усредненной плавной кривой, пересекающейся с реальной кривой в начале каждого воздействующего полупериода напряжения сети.

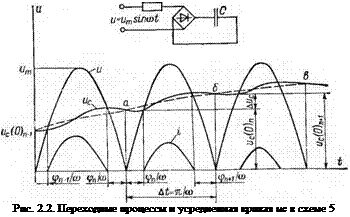
Поясним сказанное на примере переходных процессов в цепи 5, изображенных на рис. 2.2. Зарядный ток на каж­дом из полупериодов заряда протекает лишь в интервале времени, когда напряжение сети больше напряжения на конденсаторах ис. Поэтому на n-м интервале заряда, к началу которого конденсаторы уже заряжены до напря­жения Ис(0)„, момент отпирания вентилей сдвинут отно­сительно начала n-й полуволны синусоиды, как это видно из рисунка, на определенный угол <рл, связанный с вели­чиной «с(0)„ равенством

Sin <pn=Uc(0)„/«m-

Запирание вентилей наступает в момент, когда напря­жение сети вновь становится меньшим напряжения на конденсаторах, причем угол фп+і больше фп из-за увели­чения напряжения на конденсаторах к концу п-го импуль­са зарядного тока на АиСп - Изображенные на рис. 2.2 точ­ки а, б, в лежат на пересечении кривой ис с вертикалями, восстановленными из начала каждого полупериода напря­жения сети. Плавную кривую ис (штриховая линия), про­ходящую через точки а, б, в, назовем усредненной кривой роста напряжения на конденсаторах. Уравнение этой кри­вой дает усредненный закон роста напряжения на бата­рее конденсаторов. Найдем это уравнение, для чего опре­делим приращение напряжения ДиСп для любого п-го интервала заряда Т в общем виде как функцию началь­ного напряжения для данного полупериода ис(0)„. Выра­жение

(я + 0 т

= J *..) (2.2)

пТ

может быть найдено обычными методами. Для этого не­обходимо рассмотреть включение линейной цепи на на­пряжение синусоидальной формы при ненулевых началь­ных условиях «с(0)„ и найти решение для промежутка времени, на протяжении которого вентиль находится в проводящем состоянии. При длительных процессах заряда напряжение ыс(0)„ в выражении (2.2) можно заменить равным ему по значению напряжением, соответствующим усредненной кривой, И, переходя ОТ дискретных Д«Сп и Ос(0)„ к непрерывно изменяющимся Д«с и ис, а также рассматривая в качестве переменной величину ucIUm, мож­но переписать выражение (2.2) в виде

AUc=umF(uc/um). (2.3)

Уточним, что понимается под переходом к непрерывно изменяющимся величинам, связанным с усредненной кри­вой напряжения на конденсаторах Uc. Каждому значению Uc можно поставить в однозначное соответствие опреде­ленное значение <р. Взяв иа усредненной кривой любую точку, проведем через нее прямую, параллельную оси абс­цисс, до пересечения с полуволной синусоиды напряжения источника питания. Угол сдвига фазы точки пересечения относительно начала полуволны синусоиды дает нам зна­чение ф, соответствующее выбранному значению Uc■ При этом функциональная связь между рассматриваемыми не - 34

прерывно изменяющимися величинами имеет ВИД Uc= =«m sirup, что совпадает с уравнением (2.1) при формаль­ном переходе от дискретных величин к непрерывным.

Для усредненной кривой роста напряжения на конден­саторах справедливо следующее очевидное равенство:

duc Дис

чг~~кг

где для любой зарядной цепи с активными токоограничи­тельными элементами и числом пульсаций, равным т, ве­личина

Д/=2я/(/лю) (2.5)

представляет собой интервал времени между точками, в которых усредненная кривая пересекается с реальной кри­вой напряжения на конденсаторах. Интегрируя уравнение (2.4), получим

*з "С ном

Іш= І Р-6)

о “СО

Здесь t3— время заряда, отсчитываемое от начала процес­са; «со — начальное напряжение на конденсаторах, в об­щем случае не равное нулю; иСном — номинальное напря­жение, до которого осуществляется заряд.

Подставляя в уравнение (2.6) выражения (2.3) и (2.5), запишем уравнение усредненной кривой в виде

(2.7)

 

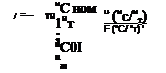Формула (2.7) справедлива для любых зарядных це­пей, и в нее можно подставить как точные, так и прибли­женные выражения функции F. В большинстве случаев указанные интегралы не выражаются через элементарные функции и могут быть решены численными или графиче­скими методами. Целесообразно, введя безразмерное время

t*3=mt3/{RC), (2.8)

строить графики t* как функции отношения «с/«т в без­размерных осях координат. Полученные таким образом безразмерные кривые справедливы для всех зарядных це­пей данного типа, не зависят от величин R к С данной цепи и могут быть использованы для определения одной из величин R, t3 и Uc/Um при заданных остальных.

Для однофазных схем 1—5, изображенных на рис. 2.1, процессы на интер­валах, когда вентили нахо­дятся в проводящем состоя­нии, описываются одним и тем же дифференциальным уравнением. Отличия за­ключаются лишь в числе пульсаций. Рассмотрим про­цесс заряда конденсаторов для любой из этих схем в течение п-го полупериода напряжения сети в середине процесса заряда, когда на конденсаторах уже имеется напряжение «с(0)„, являю­щееся начальным для данного полупериода. Рассмотрение и весь последующий анализ будем проводить при допу­щениях об идеальности неуправляемых вентилей и заряд­ного трансформатора, отсутствии утечек у конденсаторов, а также для процессов заряда, протекающих относительно медленно — в течение большого числа полупериодов пере­менного тока. Учтем также, что циклы заряд — разряд пе­риодически повторяются с частотой f.

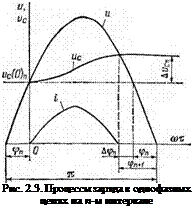
Процессы на выбранном интервале заряда иллюстри­руются рис. 2.3. Условимся время т отсчитывать от начала п-го импульса тока. Зависимость между углом сдвига <рге и величиной «с(0)„ определяется формулой

где ит — максимальное (амплитудное) значение напряже­ния сети.

Второе уравнение Кирхгофа для рассматриваемой цепи на интервале, когда вентили находятся в проводящем со­стоянии, при включении цепи RC на напряжение синусои­дальной формы при ненулевых начальных условиях «с(т=о)=«с(0)п и в момент, когда напряжение сети равно ис(0)п, имеет вид:

ис (Х)п + W - и<Гс11~)П = Um sin (№Х + ?п)’ (2-1°)

duc(t)n

где С —— = і — зарядный ток.

Решив уравнение (2.10), найдем значение напряжения на конденсаторах в любой момент времени т:

ис (х)« = tsin (шх + ¥«)-“ cos + ?и) +

сох

“Ь а (cos ¥„-}-« sin <р„)] е (2.11)

где а—RCiо — безразмерный параметр.

Процесс заряда на п-м полупериоде прекращается, ког­да ток проходит через нулевое значение, в момент време­ни Тп, равный (рис. 2.3)

т„= (2.12)

В этот момент времени напряжение на конденсаторах становится равным напряжению сети, вентиль запирается и напряжение на конденсаторах сохраняется неизменным до следующего импульса зарядного тока. Угол фп+і при длительном процессе заряда отличается от угла ф„ на небольшую величину А(рп:

Фп+1—фп+Афп - (2.13)

Как следует из рис. 2.3, для определения приращения напряжения на конденсаторах АиСп существует простая формула

AuCn — um(sinq>n+i—5ІПфп). (2.14)

Подставляя сюда значение ф„+і из (2.13) и считая, что при малом значении Дф„ справедливы приближения:

sin Афп^Дф„; cos Аф„^1, (2.15)

получим

AUcn^=Mm COS фпАфп* (2.16)

Для определения Дфп воспользуемся уравнением заряд­ного тока, которое может быть получено путем дифферен­цирования выражения (2.11): dt/c СйСит (-

Ї (х)«=с Ж^Т+Т* [cos ('шх + ¥„) + « sin (®* + ¥„) -

Из условия равенства тока нулю в момент времени, определяемый формулой (2.12), и учитывая (2.13), после несложных преобразований получим

a sin (<р„ + Д <р„) - с os (<р„ + Аф„) -

,-2Фя-Д9<|

— (cos<p„-{-asin¥>„)£ а =0. (2-18)

Учитывая приближения (2.15) и считая, что при ма­лом Афц

Дір-

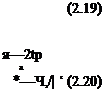і+іь.

1 а

из уравнения (2.18) найдем

я — 2ср..

___ COS уя (1 ~{~ & К ) —а sin уп ( 1 — 6 а )

Г _!z!!s

[° — ~е “ +tg¥;

( 2Ф / *ф 1 cosyyl-j-g а j — gslnyVl —е “ ) я—2ф

Подставляя последнее выражение в (2.16) и переходя к непрерывно изменяющимся Д«с и ф, найдем

Здесь Дис является функцией угла ф, связанного с усред­ненным, непрерывно изменяющимся напряжением на кон­денсаторах зависимостью

5ІПф=цс/«т, (2.22)

где осуществлен переход от дискретных фп и «с(0)п к не­прерывным. При выводе уравнения усредненной кривой из­менения напряжения на конденсаторах целесообразно в интеграле (2.7) произвести замену переменных и соответ­ственно изменить пределы интегрирования. При этом учтем, что на основании уравнения (2.22)

и выражение (2.21) представляет собой функцию F из уравнения (2.3). Подставив выражения (2.21) и (2.23) в уравнение (2.7) и умножив правую и левую части послед­него на m/(RC), получим уравнение усредненной кривой заряда конденсаторов

ф»°м 1 -^2 tgf (t

Г 1—зг* +-ТЧ1-* “ )

• = 2« 7----------------------- 7----- (2'

V. Р + » “ * )

Здесь t*3 — безразмерное время, для которого справедли­во уравнение (2.8); ф0 и фНОм — углы, соответствующие ве­личинам Uco/Wm И Нс ном/

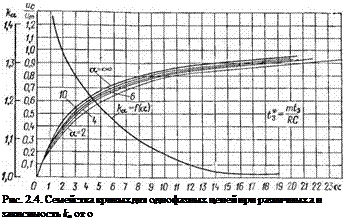Уравнение (2.24) дает возможность построить семейст­во кривых заряда для различных значений параметра «. Это семейство кривых приведено на рис. 2.4. На оси орди­нат вместо угла ф отложена более удобная для использо­вания величина UcjUm, связанная с ф равенством (2.22).

t ___ (f* f* . p.__________ *з— m H з. ном * зо/’ —'

C(l*

Из рассмотрения семейства кривых видно, что кривые для а=2, 4, 6 и 10 могут быть получены путем изменения масштаба предельной кривой ц=оо по оси абсцисс в ka раз, где ka — коэффициент, постоянный для конкретного а, но различный для разных а. Зависимость ka от « приве­дена на рис. 2.4. Эта зависимость позволяет сделать за­ключение, что коэффициент ka для зарядных цепей с п^20 практически не отличается от единицы и для расчета пара­метров в этих зарядных цепях можно пользоваться кривой, которая дает возможность определить время заряда не толь­ко для заряда с нуля, но и для заряда конденсаторов с лю­бым начальным значением «со - Используя фомулы

где t*з. ном и /*30 — безразмерное время, которое определяет­ся по кривой «=оо на рис. 2.4 соответственно для ординат исиом/Um и Uco/Щп, можно определить время заряда /3 при заданных величинах R, С, иСо и «сном либо сопротивле­ние резистора, если заданы t3, С, «со и ис ном. В формулах

(2.25) и (2.26) т= 1 для схемы 1 и т=2 для схем 2—5. Эти формулы справедливы при а^20, что имеет место в большинстве случаев на практике. При меньших значе­ниях а необходимо учитывать, что масштаб величины ^*з. ном t*зо, как было показано выше, возрастает в &араз.

Для определения энергии потерь в однофазных заряд­ных цепях с активными токоограничительными элемента­ми проще всего воспользоваться методом динамических вольт-амперных характеристик, предложенным И. В. Пен - теговым [8]. Динамические вольт-амперные характеристи­ки можно получить, подав на пластины горизонтального отклонения осциллографа напряжение, пропорциональное ис, а на вертикальные — сигнал, пропорциональный току заряда і. Площадь, заключенная между кривой вольт-ам - перной характеристики и осью абсцисс, для любой заряд­ной цепи, в которой ток не разветвляется, будет пропор­циональна энергии потерь в зарядной цепи. В общем виде энергия потерь W для схем 1—5 определяется по формуле

"С hoy

W=RCk3 f Im(uc)duc, (2.27)

"СО

где k3 — специально введенный общий коэффициент запол­нения, равный отношению площади, ограниченной кривой вольт-амперной характеристики и осью абсцисс, к площа­ди, ограниченной треугольником, катеты которого есть оси ординат и абсцисс, а гипотенуза — касательная к макси­мальным значениям вольт-амперной характеристики.

Вольт-амперные характеристики цепей 1—5 одинаковы при одинаковых параметрах R и С. Закон изменения ам­плитуд импульсов тока на вольт-амперной характеристике при длительных процессах заряда может быть получен из второго уравнения Кирхгофа:

/»(*^-^р-=5-( 1 -sinT), (2.28)

составленного для рассматриваемых зарядных цепей в мо­мент времени, когда импульсы зарядного тока достигают своего максимального значения. Уравнение (2.28) доказы­вает, что огибающая вольт-амперной характеристики пред­ставляет собой прямую линию. Отсюда следует, что пло­щадь S вольт-амперной характеристики в рассматривае­мом случае равна произведению площади описанного тре­угольника на общий коэффициент заполнения к3, меньший единицы. Подставив (2.28) в (2.27) и учитывая, что k3= 40

=л/4 (вывод здесь не приводится), получим выражение для подсчета энергии потерь в схемах 1—5:

W^=^C(um-uCQf - («т-«Сном)2]. (2.29)

Легко подсчитать, что при полном заряде от 0 до ит энергия потерь составит

W,-5=0,39Cu2m. (2.30)

Это выражение представляет собой предел, к которому стремится количество энергии, выделяемое в виде тепла в активном сопротивлении зарядной цепи при полном за­ряде и а-»-оо. Как известно, потери при полном заряде от источника постоянного напряжения равны 0,5Си-т - Таким образом, потери при заряде конденсаторов через резистор и выпрямитель от однофазной сети переменного тока в общем случае в 1,29 раза меньше, чем при включении цепи RC под постоянное напряжение, но все же достаточно ве­лики.

Расчетная мощность токоограничительного резистора PR может быть-вычислена по формуле

Рв=щ, (231)

где /= 1/(£гКп) — частота следования зарядных циклов; t„ — время паузы между зарядными циклами.

Расчетное значение среднего квадратического (дейст­вующего, или эффективного) значения зарядного тока можно легко получить, используя выражение (2.31):

I^VwfjR. (2.32)

Мощность вторичной обмотки однофазного зарядного трансформатора будет равна

Р2 = Пэф^эф. з> (2.33)

где иэф '■— umjY2-

Определив потери W по формуле (2.29), можно легко рассчитать другие параметры зарядной цепи по формулам (2.31)—(2.33). Так, для схем 1, 2, 4 и 5 расчетная мощ­ность резистора при периодически повторяющихся циклах заряда равна

w..,—<2-з4>

Для схемы 3 мощность PR для каждого из резисторов в два раза меньше значения, определяемого по формуле

41

(2.34), так как та же энергия потерь распределяется по­ровну между двумя резисторами.

Конечный ВИД формул ДЛЯ Определения /Эф. з и Р2 в схемах 1—5 будет различным в связи с тем, что в схемах 4 и 5 через конденсатор С в любой момент времени течет тот же ток, что и во вторичной обмотке зарядного транс­форматора, в схемах 2 и 3 ток в каждой из половин вто­ричной обмотки зарядного трансформатора течет только в полупериоды одной полярности и каждая из обмоток работает с ПВ=50%, в схеме же 1 ток во вторичной об­мотке протекает лишь в одну из полуволн сетевого напря­жения. Учитывая это и одинаковые условия заряда для всех цепей, найдем действующие токи и мощность зарядно­го трансформатора для схем 1—5 (индекс в скобках обо­значает номера схем, к которым относится рассматривае­мая величина):

г г п

* эф. 3(4 » б) * эф2 (4 . б) 1 эф1 (4. б)

(2.36)

Ршіш. .) = «Эф(з. 2)/эф2(2. 2, = 2«зф(6, (2-37)

п р

1 Зфі(2, 3) 1 зфі(ї)>

1<2. з)=иэф^ эф1<2, г)—иэф! эф1<5) Prlt)'

Рік. з) + р*(ї. «) n /1+КТ

-------- 2--------- = Рт<*> [----- 2--- ) =

^Эф. з(і> ---- ^Эф2 (l) Г 2 /Эф. з(6),

Pj(i) ^эф^эфгЫ У 2 Рт(ь)'

Здесь /эф2 — действующий вторичный ток зарядного транс­форматора; /'Эф, — действующий приведенный ко вторич­ной обмотке первичный ток зарядного трансформатора; Р, и Р2 — соответственно расчетные мощности первичной и
вторичной обмоток зарядного трансформатора; Рт — рас­четная (габаритная) мощность зарядного трансформатора.

Расчетная мощность трансформатора для схемы 1 не находилась, так как для этого необходимо учитывать зна­чение намагничивающего тока, которое в этой схеме вели­ко в связи с односторонним протеканием тока. Очевидно, что эта мощность будет значительно превышать аналогич­ную для схем 4 и 5, поэтому применение зарядной цепи 1 нецелесообразно.

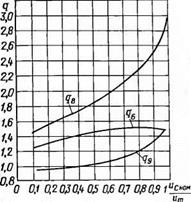
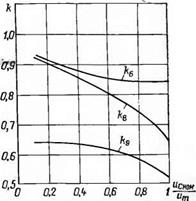
Рис. 2.5. Зависимость коэффициентов k и q табл. 2.1 от «с ном/ып.

Расчеты параметров токоограничительного резистора, токов и мощностей для трехфазных схем 6—9 носят слож­ный характер, отличаются от расчетов аналогичных вели­чин для схем 1—5 и здесь не приводятся. Результаты же этих расчетов сведены в табл. 2.1, где приведены отноше­ния ряда параметров в различных цепях к соответствую­щим параметрам в зарядной цепи 5 при одинаковых усло­виях заряда, т. е. при одинаковых значениях t3, С, иСном/Um, а также при «со=0- Все эти отношения представ­ляют собой либо постоянные числовые величины, либо функции безразмерных параметров q и ft, которые, в свою очередь, при исо=0 являются функциями одной перемен­ной Чсном/Чт и изображены на рис. 2.5 в виде кривых. Зная параметры какой-нибудь одной зарядной цепи, можно с помощью таблицы и кривых рассчитать параметры любой другой зарядной цепи, при которых обеспечиваются те же условия заряда. Единственное, что сужает возможности применения таблицы, это то, что она справедлива для слу-

		Номер схемы
Параметр	Обозначе­ ние	1	2	3	4	5	6[1]	7**	8	9
Число фаз								a
Число пульсаций	—	1		2				3	є
Сопротивление каждо-	R[2]	1/2		1			Ч,	3/2	9.	9.
го из резисторов
Мощность каждого из	р'р		1 1/21		9«ft2	1/3	Qtfi18	9.*а.
резисторов
Действующий заряд­ный ток	^ эф. з	V2		1			*.	—	^8	—
Действующий вторич-	'%ф«	VT	llV2 |			к./УГ	vT/з	/fft,	ft.
ный фазный ток						Vf *
Деііст іующий первич-	^*эф1	__		1			2/3		ft.
ный фазный ток
Начальная амплитуда	"т	2		I			1/9.	2/3	1/9.	1 7Г=- Я в
тока через вентиль Зарядный трансформа-									КЗ
тор;
пиковая мощность	Р	VT		1			0,55	0,362	0,638	1
фазы							9.		9.	3q9
суммарная мощ-	Р*.	V2				2ft.	1,63	VTfta	VTk,
ность вторичных обмоток
суммарная мощ-	Р* і	—		1			vTft,	1,13	VTfte	УГк,
ность первичных обмоток
расчетная мощ-	г Р'г+Р'*				1	1,71ft,	1,39	У 2"ft.	Узь.
ность

фазных обмоток, расположенных на различных стержнях трансформатора. При этом в половинах вторичных обмо­ток, расположенных на каждом стержне, протекают токи противоположного направления и МДС, соответствующие постоянным составляющим ^

этих токов, взаимно компенси­руются. Трансформатор маг­нитоуравновешен.

____ ц;/ j i<?c

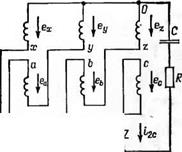
2.1 (последняя строка) и рис. 2.5 позволяет сделать вы­вод, что при заряде до «с Hov/«m^0,77 минимальные расчетные мощности, габа­риты и массу имеет трансфор­матор в зарядных цепях 4 и 5. При заряде до ис НОМ 1ит> 0,77 наименьшую расчетную мощ­ность имеет зарядный транс­форматор в цепи 9; зарядная цепь 8 в этом смысле не - $ сколько уступает цепи 9 и имеет меньшую, чем в це - рис. 2.6. Зарядная пях 4 и 5, расчетную мощ - включением ность зарядного трансформа­тора лишь при соотношении Uc ном 1ит>0,85. Расчетные мощности зарядных трансфор­маторов в схемах 1, 2, 3, 6, 7 значительно превышают ана­логичные в схемах 4, 5, 8, 9, и поэтому применение заряд­ных цепей 1, 2, 3, 6, 7 связано с существенным проигры­шем в габаритах и массе всего зарядного устройства.

Представляет интерес зависимость расчетных мощно­стей трансформаторов от Нсном/пт для каждой схемы. В частном случае заряда при «со = 0 расчетная мощность трансформатора для схемы 5 может быть рассчитана по формуле (2.36). При исо=0 величина /3о=0 и формула (2.36) приобретает вид

Р, ы = 1/-^Си'с^м - (2-43)

где Р*т(5) — расчетная мощность зарядного трансформато­ра в относительных единицах, являющаяся безразмерной функцией ис нон/ит и равная

1/

У 32
/"Си,

Поэтому отношения, полученные для Рт при одинако­вых условиях заряда, справедливы и для Р*т.

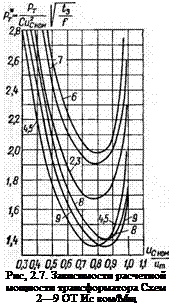На рис. 2.7 по уравнению (2.44) построена кривая 4, 5, показывающая, что при Исном/Ыт=0,8 расчетная мощ­ность зарядного трансформа­тора имеет минимальное значе ние. Также и для всех зарядных цепей существуют условия за­ряда, при которых расчетная мощность зарядного трансфор­матора минимальна. Миниму­мы всех приведеннных кривых лежат внутри интервала 0,8-^ ^«с ном/Ыт^О,9, причем рас­четные мощности зарядных трансформаторов для схем 2—7 минимальны при «Сном/«т=0,8, для схем 8 и 9—при «сном/ыт=0,85. Из вентильных схем наиболее вы­годной является схема 9, так как она обеспечивает наимень­шую расчетную мощность трансформатора при наиболь­шем значении «сном/Um, что позволяет получить минималь­ные габариты и массу всего зарядного устройства.