Ниже будет показано, что при скоростях v > 10 и размере пятна rQ < 5 за время прохождения пятна над рассматриваемой точкой теп­лота распространяется на глубину, меньшую толщины стенки. В этом случае можно рассматривать нагрев полубесконечного тела, поэтому Г, Хг0

= —q— зависит только от скорости:, Т^ = f(v).

Условия v > 10 и S > rQ в плазмотронах обычно выполняются.

Скорость перемещения дуги относительно электрода составляет

10.. . 100 м/с, а радиус пятна 1...5 мм. Тогда для медных электродов получим

vr

V = —1— = 44...2200.

2а

Задача распространения теплоты от движущегося кругового ис­точника решена Н. Н. Рыкалиным с использованием метода источников и

Т,

0,06 0,04

о, ог о

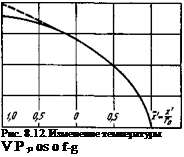
по диаметру пятна при V = 20:

--------- круговой источник; —

нагрев стержня за время Т

ХІи;Тл

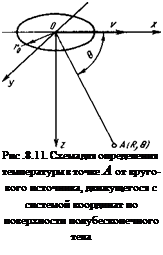
принципа взаимности. В подвижной системе координат, связанной с центром источника 0 (рис. 8.11), температура в произвольной точке в плоскости у = 0 определяется по формуле

Г Хг 1 я - о{х +R )

10 1 f —у - f е *

—Q— = — ! rdr!------------------ ------------- dp.

w я о о R

В качестве примера на рис. 8.12 приведено распределение тем­ператур на поверхности полубесконечного тела вдоль оси х при v - = 20. Для каждой точки двойной интеграл находился численным ме­тодом. Видно, что максимум температуры расположен на краю источ­ника, противоположном направлению движения.

Рассмотрим одномерную задачу нестационарного нагрева полубес­конечного тела под действием постоянного удельного теплового потока

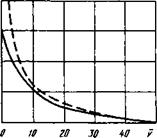
Рис. 8.13. Сравнение зависимости jF температуры на краю источника от

скорости его движения: ЦМ

------ круговой источник; ...................... на­грев теплоизолированного стержня qrf

ЦМ

Будем считать, что за время пробе­гания источника над данной точкой Qos процесс распространения теплоты бу­дет такой же, как в полубесконечном теплоизолированном стерж­не, нагреваемом в течение времени т = — тепловым потоком q.

Температура на поверхности стержня определится выражением

Подставляя т = — и приводя к безразмерному виду, получим

2х

-3

я »г„

Очевидно, что при определении температуры по формуле (8.2) на краю источника при х = 2rQ температура будет несколько завышена.

Однако ошибка уменьшается с ростом скорости. На рис. 8.12 приве­дены распределения температур вдоль источника при v = 20, рассчи­танные по формулам (8.1) и (8.2). Видно, что при о » 20 точность определения температуры по простой формуле (8.2) вполне доста­точна. На рис. 8.13 дано сравнение температур на краю источ­ника, рассчитанных по формулам (8.1) и (8.2), которое подтверждает этот вывод. Если точка, в которой определяется температура

расположена на оси Z и р > 10, то температура может быть опре­делена по формуле

Рис. 8.14. Изменение температуры по

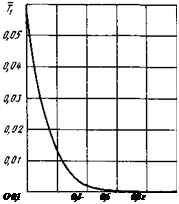оси, проходящей через центр источ­ника, перемещающегося со скоростью

V ш 20

Рассчитанное по этой формуле рас­пределение температур по оси г при

v = 20 показано на рис. 8.14. Видно, что на глубине z = 0,5rQ повышение

температуры от действия источника пренебрежимо мало. Толщина стенки электрода обычно превышает 0,5г^, поэтому при v > 20 можно поль­зоваться формулами, полученными для полубесконечного тела.

Приведем формулу (8.2) в размерном виде

2-2а

3

я or.

Из полученного выражения видно, что температура Г слабо за­висит от силы тока и сильно зависит от плотности тока. Она может быть уменьшена до допустимого значения за счет создания необхо­димой скорости перемещения источника.