Next, we discuss the recombination dynamics as a function of time. Consider a semiconductor subjected to photoexcitation. The equilibrium and excess electron and hole concentrations are n0, p0, An, and Ap, respectively. Since electrons and holes are generated and annihilated (by recombination) in pairs, the steady-state electron and hole excess concentrations are equal,

A n(t) = A p(t) . (2.4)

Using the bimolecular rate equation, the recombination rate is given by

R = B [n0 + An(t)] p0 + Ap(t)] . (2 5)

For the case of low-level excitation, the photogenerated carrier concentration is much smaller than the majority carrier concentration, i. e. An << (n0 + po). Using An(t) = Ap(t) one obtains from

Eq. (2.5)

(2.6)

R = Bn2 + B (n0 + p0) Аn(t)

:xcess •

= R0 + Rexcess.

The first summand on the right-hand side of the equation can be identified as the equilibrium recombination rate (R0) and the second term as the excess recombination rate (Rexcess).

The time-dependent carrier concentration can be calculated from the rate equation

dn(t) dt

(2.7)

G R (0 + Gexcess) ( + Rexcess)

where G0 and R0 are the equilibrium generation and recombination rates, respectively.

Next, we assume that the semiconductor has been illuminated with light and excess carriers are generated. At the time t = 0, the illumination is switched off (i. e. Gexcess = 0) as indicated in Fig. 2.2. The recombination rate can then be calculated by insertion of Eq. (2.6) into Eq. (2.7) and using G0 = R0. This yields the differential equation

(2.8)

The solution of the differential equation can be obtained by separation of variables. One obtains

(2.9)

А n(t) = А n0e - B(n° + p0)t

where An0 = An(t = 0). Rewriting the result as

(2.10)

Аn(t) = Аn0 e {^T

allows one to identify the carrier lifetime т as

(2.11)

т

1

B (n0 + p0)

For semiconductors with a specific doping type, Eq. (2.11) reduces to

1

1

(2.12)

т

n

Bp0

BNa

for p-type semiconductors

and

1

1

(2.13)

Tp =

Bn0

BN

D

for n-type semiconductors

where Tn and Tp are the electron and hole lifetimes, respectively. Using this result, the rate equation, Eq. (2.8), can be simplified for semiconductors of a specific conductivity type. One obtains the monomolecular rate equations.

d. , ч Аn(t)

for p-type semiconductors

(2.14)

А n(t) =------------------ ^-

dt Tn

and

d А p(t)

for n-type semiconductors.

(2.15)

А p(t) = til.

dt тг

p

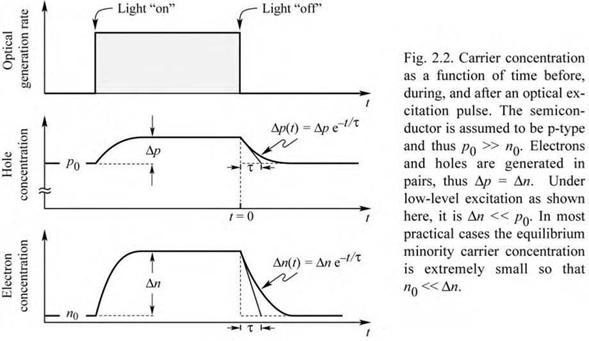
Figure 2.2 shows the majority and minority carrier concentrations in a p-type semiconductor as a function of time (similar considerations apply if an n-type semiconductor is chosen). Note that Fig. 2.2 shows the case of low-level excitation in which the photogenerated carrier

concentration is much smaller than the majority carrier concentration. However, the photogenerated carrier concentration is much larger than the minority carrier concentration.

Once photoexcitation is terminated, the minority carrier concentration decays exponentially with a characteristic time constant denoted as the minority carrier lifetime т. It is the mean time between generation and recombination of a minority carrier.

Note that the majority carrier concentration also decays with the same time constant т. However, only a very small fraction of the majority carriers disappear by recombination, as illustrated in Fig. 2.2. Thus, for low-level excitation, the average time it takes for a majority carrier to recombine is much longer than the minority carrier lifetime. For many practical purposes, the majority carrier lifetime can be assumed to be infinitely long.

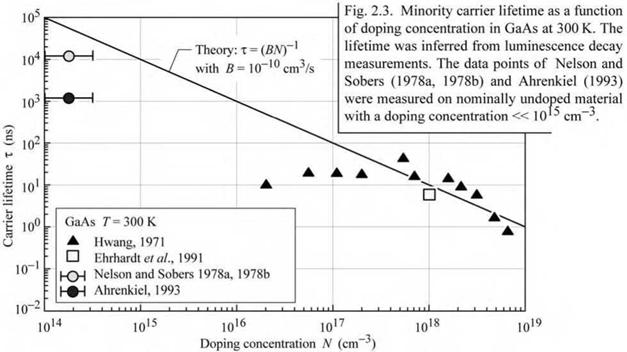
Theoretical and experimental values for the minority carrier lifetime in GaAs as a function of the doping concentration are shown in Fig. 2.3 (Hwang, 1971; Nelson and Sobers, 1978a, 1978b; Ehrhardt et al., 1991; Ahrenkiel, 1993). The theoretical line in the figure is calculated from Eq. (2.10) using B = 10-10 cm3/s. In nominally undoped material, minority carrier lifetimes as long as 15 |j, s have been measured in GaAs at room temperature (Nelson and Sobers, 1978a, 1978b).

Exercise: Minority carrier lifetimes. Calculate the minority carrier lifetime in p-type GaAs at doping concentrations of 1015 and 1018 cm-3 using a bimolecular recombination coefficient of B = 10-10 cm3/s. Assume that one could fabricate GaAs without any impurities. What would be the carrier lifetime in intrinsic GaAs with a carrier concentration of 2 x 106 cm-3 ?

Solution: Tn = 10 ^.s for NA = 1015 cm3

Tn = 10 ns for Na = 1018 cm3

t = 2500 s for undoped GaAs.

Discuss how the modulation speed of communication LEDs is affected by the radiative lifetime and the doping concentration.

2.1 Radiative recombination for high-level excitation For the case of high-level excitation, the photogenerated carrier concentration is larger than the equilibrium carrier concentration, i. e. An >> (n0 + p0). The bimolecular rate equation (Eq. 2.3) is then given by

<>А"« = - B Ап2 . (2.16)

dt

Solving this differential equation by the separation-of-variables method and using the initial condition A"(0) = A"0 yields the solution

(2.17)

А"^) = 1

Bt + А"0

This solution represents, in contrast to the low-density approximation, a non-exponential carrier decay.

In an exponential decay, it takes the time constant т for the carrier concentration to decrease from An0 to A"0 e-1. Using the same definition for the non-exponential decay given by Eq. (2.17), the “time constant” can be calculated from the slope of the decay by using the equation

T(t) = - Hk (218>

dt

Using this definition for the non-exponential decay of Eq. (2.17), one obtains the “time constant”

T(t) = t + ^7— • <219)

B 7n0

Thus, for non-exponential decays, the “time constant” depends on time. Equation (2.19) shows that the minority carrier lifetime increases with time. For sufficiently long times, low-level excitation conditions will be reached and т will approach the low-level value.