Рассмотрим реализацию расчета тепловых и деформационных задач на примере программного комплекса «СВАРКА», разработка которого на­чата на кафедре сварки МГТУ им. Н. Э. Баумана в 1974 г. и продолжается в настоящее время. Действующая версия 4.0 (1999 г.) ориентирована на рабо­ту в среде Windows персонального компьютера.

Работа происходит в основном в диалоговом режиме. Основной экран, появляющийся при запуске программы (рис. 2.9), имеет традиционное оформление Windows с раскрывающимся меню вверху, панелью информа­ции внизу и кнопками панелей инструментов по периметру справа и слева (панели справа сменные). Поле экрана обычно разбито на две части: квад­ратную слева для графических изображений и узкую справа для текстовой и цифровой информации. Эти части относятся к одному и тому же объекту' и дополняют друг друга, редактирование данных можно проводить как в гра­фической, так и в текстовой части окна. Возможно изменение через меню размера всего окна и его частей в процессе работы.

Работа начинается с открытия нового или сохраненного проекта. Про­ектом в комплексе называется совокупность исходных данных и результа­тов моделирования для конкретной модели. При открытии нового проекта работа с его данными начинается с самого начала (все результаты предыду­щих расчетов стираются). При открытии сохраненного проекта восстанав­ливается на экране то его состояние, которое было на момент прекращения

СВАРКА [СВАРКА 11

ЗАЯАМА Геогч*ТрИА,'ММЧфМСІЛ Т»ПГ^Е-Иір4.’>ЗИАУ ЧвьйНЙХЛ :Р*гул»тать» С*КО ПОМЙІЧЬ ''

РАЗМЕРЫ КАРКАСА Размер Значение

га

00.00 (50.00-150.01

_D & в

&>

Ar**ofy.('V!«j»st»Vs«'Jh іЙ^ГІонюІцьч /

**»©«« »*».■» амвсе*>*о» 4 I - |

>j***3323«h ^ і>,іОШмм

’ііСПуоі} й|{Е<Ря#с«'яі)_| By Mtooio»Vfef0.:.| Qitob. Fjittta-.. | jgbawawtbni-[ 58МотмЙіРєуєаД^ C8APKA-{С...

Рис. 2.9. Диалоговое окно комплекса «СВАРКА»

предыдущего сеанса работы с ним. Можно начать работу с просмотра полученных ранее результатов или продолжить моделирование с изме­ненными граничными условиями от любого из уже выполненных шагов.

Построение геометрической модели. Предусмотрены две стадии по­строения геометрической модели детали. Первая стадия выполняется ква­лифицированным пользователем и позволяет построить любую модель.

В процессе построения определяются не только внешние контуры де­тали, но и ее внутреннее разбиение на элементы. Одновременно вводится информация о зонах из различных материалов в пределах детали и прово­дится подготовка к заданию граничных условий для модели.

Второй этап предназначен для работы новичка или для выполнения вариантов расчета на однотипных моделях. Он позволяет, выбрав одну из уже построенных моделей, в графическом режиме редактировать ее размеры и количество элементов в ней.

Рассмотрим структуру модели и этапы ее построения. Разбиение на этапы позволяет выполнять построение не сразу, а постепенно, чтобы после

каждого этапа можно было увидеть изображение построенной части модели. Это облегчает поиск и исправление ошибок.

Основным средством построения модели является блок. Он служит для выделения части объема модели вместе с ее содержимым (материалом).

Простои объемный блок предназначен для моделирования массивных тел. В общем случае он имеет вид деформированного кубика, ограниченно­го шестью гранями, каждая из которых является частью поверхности. Все грани одного блока должны принадлежать разным поверхностям. Каждая грань представляет собой в общем случае деформированный четырехуголь­ник, ограниченный четырьмя ребрами, каждое из которых является частью линии. Все ребра одной грани должны принадлежать разным линиям. Каж­дое ребро является в общем случае пространственной кривой, вид которой задают координаты лежащих на ней узлов. На ребрах простого блока можег быть два или три узла (два из них лежат на концах ребра и являются вер­шинами блока, а третий — на середине ребра). В первом случае ребро представляет собой отрезок прямой, во втором — отрезок квадратной па­раболы, соединяющей узлы ребра. Следовательно, в частных случаях объ­емный блок может иметь прямые ребра, быть параллелепипедом или пра­вильным кубом.

Сложный объемный блок отличается от простого наличием дополни­тельных узлов и линий на гранях и внутри блока. Узлов на ребре сложного блока может быть два или любое нечетное число более двух.

Если узлов более трех, то ребро состоит из нескольких отрезков квад­ратных парабол, каждая из которых соединяет три последовательных узла.

Для описания объемного блока (простого или сложного) необходимо перечислить номера поверхностей, ограничивающих блок.

Поверхности перечисляются в таком порядке: 1 — нижняя, 2 — пе­редняя, 3 — левая, 4 — задняя, 5 — правая, 6 — верхняя (если смотреть из­нутри блока, стоя на любой его грани).

Специальные блоки отличаются числом граней, ребер и вершин. Име­ются два вида специальных блоков: пятигранный в виде деформированной треугольной призмы и четырехгранный в виде деформированной треуголь­ной пирамиды (тетраэдра). Специальные блоки могут быть сложными. Для описания этих блоков также необходимо перечислить номера поверхностей, ограничивающих блоки.

Для четырехгранного блока порядок перечисления: 1 — нижняя по­верхность, 2 — передняя, 3 — левая, 4 — правая. Для пятигранного блока первые четыре такие же поверхности, а 5 — верхняя поверхность.

Пластинчатый пространственный блок предназначен для моделиро­вания листовых конструкций и эквивалентен по виду и устройству грани объемного блока. Простой пластинчатый блок имеет вид деформированного четырехугольника, ограниченного квадратными параболами. Частные случаи — четырехугольник с прямыми сторонами, прямоугольник, квад­рат. Каждое ребро — отрезок параболы с узлами на концах и, возможно, в середине.

Сложный пластинчатый блок отличается наличием дополнительных узлов и линий в пределах блока, он эквивалентен грани сложного объемного блока. Для описания пластинчатого блока необходимо перечислить по кругу номера четырех линий, ограничивающих блок.

Специальный пластинчатый блок имеет вид деформированного тре­угольника и эквивалентен грани объемного четырехгранного блока, он мо­жет быть сложным. Для его описания необходимо перечислить номера трех ограничивающих блок линий.

Плоский блок для моделирования плосколистовых и осесимметричных тел, а также массивных протяженных тел, имеющих в направлении третьей координаты неизменную геометрию, неизменные граничные условия и свойства материала. Он отличается от пластинчатого тем, что все плоские блоки лежат в одной плоскости и их узлы имеют нулевую третью координа­ту. При перечислении линий, ограничивающих плоский блок, следует соблю­дать направление обхода блока против хода часовой стрелки.

Стержневой блок предназначен для моделирования стержневых кон­струкций. Он эквивалентен ребру объемного или пластинчатого блока. Про­стой стержневой блок имеет вид отрезка параболы или прямой с узлами по концам и в середине отрезка.

Сложный стержневой блок имеет дополнительные узлы, соединен­ные по три отрезками параболы, и может иметь форму любой лекальной кривой, а также изломы в узлах.

Для описания стержневого блока необходимо перечислить номера двух узлов на его концах.

Каждый блок, так же как каждая поверхность, линия и узел, имеет свой номер. Все блоки нумеруются по порядку, начиная с № 1. Если в модель вхо­дят блоки разных видов, то вначале нумеруются объемные, далее пластинча­тые, затем стержневые блоки. В процессе построения модели номера блоков могут измениться вследствие их разбиения на более мелкие блоки. Сложные и специальные блоки используются для уменьшения числа вводимых блоков. При дальнейшем построении они разбиваются на простые блоки.

Для моделирования деталей с неоднородностью может быть указан но­мер материала каждого блока. Какой именно материал соответствует каждо­му из номеров, уточняют на следующих этапах построения модели детали. Отрицательные номера материалов предназначены специально для моделиро­вания процесса многопроходной сварки. Они позволяют указать, какая группа элементов разделки заполняется металлом при очередном проходе.

Поверхность состоит из линий. Для описания поверхности необходи­мо перечислить номера лежащих на ней линий (в любом порядке). Поверх­ность может быть плоской или неплоской, в зависимости от геометрии линий.

Основное назначение поверхностей — описание объемных блоков. В связи с этим на поверхности накладываются следующие ограничения:

• поверхность может включать одну или несколько граней объемных блоков и пластинчатые блоки, но не должна включать две грани одного и того же блока;

• поверхность не должна проходить дважды через одну и ту же линию (самопересечение поверхности не допускается);

• не допускаются замкнутые поверхности (в этом случае поверхность следует разбить на части);

• две поверхности могут иметь одну общую линию (линию пересечения);

• двойное пересечение поверхностей не допускается.

Поверхности нумеруются в произвольном порядке, начиная с № 1.

Эти номера не изменяются в процессе построения модели. Новые поверхно­сти добавляются в конец списка.

Линия состоит из узлов. Для описания линии необходимо перечислить номера всех ее узлов в том порядке, в котором они лежат на линии, начиная с любого ее конца. Линия может быть прямой, кривой или ломаной в зави­симости от координат ее узлов.

Правила описания линий:

• линия не может дважды проходить через один и тот же узел (само­пересечение не допускается);

• замкнутая линия не допускается;

• две линии могут иметь один общий узел (точку пересечения);

• двойное пересечение линий не допускается;

• линия не может принадлежать поверхности частично, если номер линии указан при описании поверхности, значит, этой поверхности принад­лежат все узлы линии;

• общая линия двух поверхностей является линией их пересечения;

• линия не должна начинаться или оканчиваться внутри стержневого блока, ребра пластинчатого или объемного блока;

• линии, ограничивающие пластинчатый блок или грань объемного блока, должны все принадлежать одной поверхности (в плоских и осесим­метричных моделях все линии принадлежат поверхности № 1).

Линии нумеруются в произвольном порядке, начиная с № 1. Эти но­мера не изменяются. Новые линии добавляются в конец списка. Линии (хотя бы одна) должны быть введены обязательно. Для ввода прямой линии должны быть заданы два узла на ее концах; для ввода параболы необходимо задать три узла: два — по концам и один -—- в середине; более сложные ли­нии могут быть описаны любым нечетным числом узлов, но практически будут представлены в виде цепочки парабол.

Линии могут быть длинными или короткими (содержать различное число узлов). Поверхности также могут содержать различное число линий. Пользоваться короткими линиями и небольшими поверхностями проще, хо­тя это несколько увеличивает количество исходных данных. Преимущество длинных линий и больших поверхностей в том, что они позволяют описы­вать более крупные блоки. Линии и поверхности внешнего контура узла ис­пользуются при задании граничных условий. Поэтому те участки контура, на которых условия могут отличаться, должны быть описаны разными ли­ниями и поверхностями, а те, для которых условия совпадают, удобнее за­давать целиком.

Узел представляет собой точку с тремя координатами (у плоских мо­делей третья координата равна нулю). Расположение координатных осей может быть любым, но одинаковым для всех узлов модели. В осесиммет­ричных моделях первая координата направлена по радиусу, а вторая являет­ся осью симметрии.

Основные узлы размещаются на линиях и являются узлами КЭ моде­ли. Вспомогательные узлы служат для определения координат основных узлов. В число узлов на линиях можно включать, кроме тех, для которых уже заданы координаты, также узлы с последующими номерами (с неиз­вестными пока координатами) при условии, что эти координаты будут опре­делены в процессе составления модели к моменту их использования.

Узлы нумеруются в произвольном порядке, начиная с № 1. При со­ставлении модели происходит добавление узлов в конец списка. Присвоен­ные узлам номера в ходе составления модели не изменяются, за исключени­ем узлов из конца списка, которым после вычеркивания вспомогательных узлов присваиваются их номера.

Координаты узлов могут быть заданы с помощью смещения (размера) по отношению к одному из ранее введенных узлов. Размеры задаются от­дельно по каждой координате с указанием номера базового узла, имени раз­мера (до четырех символов) и списка номеров вводимых узлов. Затем для каждого имени задается исходное значение размера и (не обязательно) пре­делы его возможного изменения. Если пределы заданы, то этот размер появ­ляется на изображении модели и может быть изменен при редактировании модели в графическом режиме на второй стадии ее построения. Такая форма ввода облегчает параметризацию модели (обеспечивает изменение коорди­нат нескольких узлов при изменении одного размера).

Размеры могу т быть также введены от специального узла № 0 (ко­торый не требуется вводить) с нулевыми координатами (эти размеры

равны координатам вводимых узлов). Предусмотрен также нулевой раз­мер с именем 0.

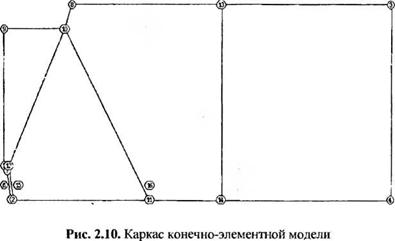
После введения узлов и линий возможна визуализация модели в виде каркасной («проволочной») основы (рис. 2.10).

Дальнейший процесс построения разбивки происходит автоматически и заключается в разбиении специальных блоков на сложные, сложных — на простые. В процессе этого разбиения в списки добавляются новые блоки, поверхности, линии и узлы. В составленной модели все блоки простые. До­полнительное уменьшение числа вводимых данных достигается за счет вспомогательных операций — ввода эллипса, дробления и сгущения.

Эллипс позволяет уменьшить число вводимых координат узлов. Коор­динаты промежуточных узлов вычисляются в программе по уравнению эл­липса. Для ввода дуги эллипса (окружности) необходимо перечислить пять узлов: три вспомогательных (в центре и на концах большой и малой полу­осей) и два основных (на концах дуги). Вместо вспомогательных узлов можно повторно использовать основные. Узлы дуги эллипса должны лежать на одной из линий.

Дробление также имеет назначение уменьшить число вводимых коор­динат. Координаты вычисляются по уравнению квадратной параболы. Дробления затем видны на изображении модели и могут быть изменены при ее редактировании на второй стадии построения модели.

Сгущение позволяет на основе ранее составленной модели получить модель с большим количеством блоков путем их дополнительного разбие­ния вблизи указанных узлов, линий или поверхностей. Для каждого сгуще­ния необходимо указать внутренний радиус (радиус отверстия, создаваемо-

Рис. 2.11. Каркас с кривыми и дроблениями

го на месте прежнего узла или линии); радиус первого яруса концентриче­ской сетки элементов и прогрессию увеличения радиусов следующих яру­сов. Ярусов столько, сколько помещается в исходных блоках, которым при­надлежали узел или линия сгущения. По умолчанию внутренний радиус ра­вен нулю, минимальный очень большой, а прогрессия со знаменателем 2.

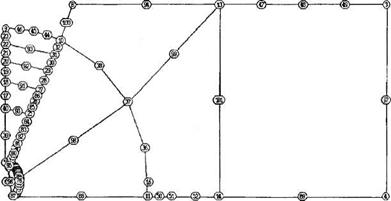
После построения каркаса (см. рис. 2.10) на ребра добавляются узлы с помощью эллипсов и дроблений. В результате некоторые ребра приобретают

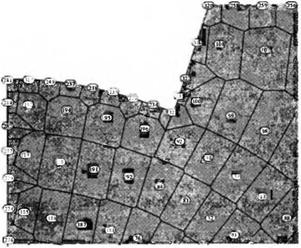
криволинейную форму. Вид модели после этого этапа показан на рис. 2.11. За­

тем производится разбиение блоков на элементы (рис. 2.12). Далее на основе

полученной сетки, пред­назначенной для расчета

напряженно-деформиро­ванного состояния (НДС), строится сетка для задач тепломассопереноса (рис. 2.13), аналогичная сетке на рис. 2.6. Общими у сеток на рис. 2.12 и 2.13 являются центры элемен­тов. В сетке на рис. 2.13 центрами элементов яв­ляются также граничные узлы сетки на рис. 2.12.

Имеется возмож­ность построения объем - Рис. 2.12. Фрагмент модели для расчета деформаций ной модели из плоской

путем разворачивания (движения) вдоль прямой или окружности (рис. 2.14).

Рис. 2.13. Фрагмент модели для расчета массопереноса

Для этого предназначен элемент данных под име­нем секции, указывающий сколько слоев и какого раз­мера нужно создать. Если исходная модель помечена как плоская, то информа­ция о секциях трактуется как линейные размеры по третьей координате в мил­лиметрах, а если модель была осесимметричная — как угловые размеры в градусах.

Предусмотрена также библиотека готовых моделей, которую можно просмотреть, использовать ее модели, отредактировав их размеры, или включать эти модели на правах блоков в создаваемую новую модель.

Встроенный в программу текстовый редактор позволяет после каждо­го этапа просмотреть отчет о ходе геометрического моделирования и пара­метры построенной модели.

Итоговая информация о геометрии модели носит традиционный для МКЭ вид. Ее основу составляют координаты всех узлов и список номеров

узлов для каждого элемента (топология). Это позволяет импортировать моде­ли, построенные вне комплекса, и экспортировать построенные в комплексе, т. е. взаимодействовать с другими конечно-элементными комплексами.

Ввод свойств материала, начальных и граничных условий. Ос­новная модель материала в комплексе «СВАРКА» представляет собой смесь нескольких компонентов с указанием процентного содержания каждого компонента. Свойства смеси определяются интерполяцией по свойствам компонентов. В связи с этим в состав данных о свойствах материалов преж­де всего входят:

• список имен компонентов;

• свойства каждого из них;

• исходный состав для каждого номера материала, введенного для блоков при создании геометрической модели детали;

• для задач сварки — состав материала, заполняющего разделку в процессе сварки.

Свойства компонентов хранятся в базе данных в табличном виде и из­влекаются из нее по именам компонентов при составлении модели. Эта база данных и система ее редактирования являются частями комплекса «СВАРКА». Предполагается дальнейшее развитие моделей поведения компонентов ма­териалов и их взаимных превращений, поэтому в базе данных предусмотрен резерв для добавления новых характеристик.

Основными теплофизическими свойствами являются теплопровод­ность и объемная теплоемкость, а также скрытая теплота при взаимном пре­вращении таких структурных компонентов сталей, как перлит, аусгенит и т. д. Расплавленное состояние тоже может быть представлено как отдельный компонент, что позволяет ввести в модель скрытую теплоту плавления. Ус­ловия превращения могут быть заданы в различном виде, например в виде температурного интервала, при прохождении которого компонент превра­щается в другой.

Набор механических характеристик определяется тем, что в комплек­се «СВАРКА» предусмотрено несколько различных моделей поведения ма­териала, основными из которых являются:

• упругопластическая с произвольным законом упрочнения, с крите­рием разрушения и постоянными механическими характеристиками;

• идеальная упругопластическая с переменными механическими ха­рактеристиками;

• вязкоупругопластическая с характеристиками, полученными в усло­виях программированного термодеформационного цикла;

• модель пористого материала.

Для того чтобы любая модель материала могла сочетаться с любой геометрической моделью, предусмотрен универсальный комплект из восьми механических характеристик материала, часть из которых может быть не задействована в конкретной модели. Все они вводятся в виде таблиц. Для каждой характеристики должно быть указано ее имя, а также ряд пар значе­ний аргумента и характеристики, являющейся его функцией. Минимальное количество пар — две, максимальное — не ограничено.

Список характеристик:

• деформационная характеристика в виде таблицы значений интен­сивности напряжений, аргумент — интегральная пластическая деформация (параметр Одквиста);

• критерий разрушения в виде таблицы значений предельной пластич­ности, аргумент — показатель объемности напряженного состояния;

• отношение предела текучести при растяжении к пределу текучести при сжатии, аргумент — температура;

• предел текучести при растяжении, аргумент — температу ра;

• моду ль упругости при сдвиге, аргумент — температура;

• объемный модуль упругости, аргумент — температу ра;

• модуль упрочнения при ползучести, аргумент — температура;

• дилатометрическая характеристика в виде таблицы значений темпе­ратурно-структурной объемной деформации, аргумент — температура.

Предусмотрен также материал «по умолчанию», соответствующий стали с очень высоким пределом текучести и свойствами, не зависящими от температуры, позволяющий пропускать ввод свойств материала в исходных данных. Он пригоден для использования в рамках любой из перечисленных моделей материала.

Все характеристики, являющиеся функциями температуры, должны иметь одинаковые области определения (крайние значения аргумента).

Для каждого физического процесса предусмотрено три рода гранич­ных условий:

1- го рода: в точках границы задана температура в тепловой задаче или перемещения в деформационной — постоянные или функции от времени;

2- го рода: задан в тепловой задаче поток теплоты, а в деформацион­ной — распределенные или сосредоточенные силы;

3- го рода (только для процессов энергомассопереноса): задана среда за границей со своими параметрами и условия взаимодействия модели с этой средой (например, коэффициент теплоотдачи с поверхности в тепловой задаче).

Г раничные условия 1-го и 2-го рода являются частными случаями ус­ловия 3-го рода. В некоторых случаях возможно непосредственное действие граничных условий на внутренние узлы и элементы модели (индукционный нагрев, гравитационные, инерционные и электромагнитные силы и т. д.).

Для моделирования сложных процессов во времени они разбиваются на шаги (конечные элементы по координате времени). На каждом шаге пре­дусмотрено задание граничных условий для отдельных узлов модели или для групп узлов. Для выделения таких групп на внешнем контуре модели служат поверхности и линии. Для векторных граничных условий (переме­щений и сил) предусмотрено задание компонентов по осям координат, по заданному направлению или по нормали к участку границы.

При выборе вида граничных условий следует учитывать, что сходи­мость решения улучшается при увеличении числа узлов с заданными гра­ничными условиями 1-го рода.

Необходимо задать начальные значения параметров для всех узлов и элементов. Чаще всего они задаются одинаковыми для всей модели или из­влекаются из информации, введенной при геометрическом моделировании. Возможно также использование функций от координат узлов модели.

Составление и решение систем уравнений. На вводе граничных ус­ловий завершается интерактивный этап моделирования, дальнейшая работа протекает автономно с периодической информацией пользователя о ходе работы. Все расчеты на интерактивном этапе приводят к переводу окна пользователя в режим ожидания. В процессе длительного счета необходимо дать ему возможность продолжать работу с моделью, просматривать порции результатов по мере их выдачи компьютером, а при необходимости — вме­шиваться в процесс моделирования. С этой целью в комплексе использована многопоточная система Windows для организации дополнительного рабоче­го потока, в котором проходит счет. В однопроцессорном персональном компьютере запу ск более одного дополнительного потока снижает произво­дительность. Поэтому запуск еще одного экземпляра комплекса или откры­тие одновременно нескольких проектов возможны, но нецелесообразны. При наличии нескольких процессоров можно существенно повысить произ­водительность решения связных задач, разделяя моделируемые параллельно процессы между процессорами компьютера.

Этап составления системы уравнений занимает время, пропорцио­нальное числу КЭ модели, начальный этап ее решения (прямая прогонка) — пропорциональное кубу числа узлов, а обратная прогонка — пропорцио­нальное квадрату числа узлов. В связи с этим операция составления матри­цы занимает основную часть времени счета при небольшом числе элемен­тов, а прямая прогонка — при большом числе. Объем памяти пропорциона­лен квадрату числа узлов. Это следует учитывать при построении модели и измельчать элементы только там, где это необходимо для обеспечения точ­ности решения (в зонах ожидаемых больших градиентов результатов).

В комплексе «СВАРКА» предусмотрено хранение системы уравнений в оперативной памяти. Использование виртуальной памяти на диске воз­можно, но при этом снижается производительность, поэтому целесообразно иметь в компьютере оперативную память, необходимую для решаемых за­дач (порядка 20 Мб для несложных плоских и осесимметричных задач и бо­лее 100 Мб для объемных).

Составление и решение системы уравнений требуется только при не­явной схеме решения, т. е. в комплексе «СВАРКА» для деформационной задачи. Она и является критической по времени и памяти компьютера. Теп­ловая задача может занять много времени при мелких элементах и длитель­ном процессе вследствие большого числа шагов.

Итерационное уточнение решения. Такое уточнение проводится всегда при неявной схеме решения, хотя реальная необходимость в нем имеется только для нелинейных задач, для очень больших по числу элемен­тов моделей, а также при некоторых других особенностях модели (напри­мер, при большой гибкости элементов). Число итераций зависит от парамет­ров точности, введенных в граничных условиях. Их три:

• абсолютная погрешность, зависящая от габаритных размеров модели;

• относительная погрешность, зависящая от изменений характеристик модели за шаг;

• предельное число итераций.

Смысл параметров точности заключается в том, что большая точность не требуется для крупных моделей и при крупных шагах решения, а также в необходимости исключить зацикливание компьютера. Меняя три параметра точности, пользователь влияет на точность решения и время его получения.

Следует отметить, что, поскольку сходимость решения обычно моно­тонная, достигнутую точность приходится оценивать косвенно, не по по­грешности, а по степени изменения результата решения за очередную ите­рацию.

Итерационный процесс построен так, чтобы обеспечивать устойчи­вость решения на каждом шаге, по мере возможности устранять все по­грешности предыдущих шагов, как связанные с нелинейностью, так и воз­никшие при составлении и решении уравнений.

При медленном монотонном изменении результатов итераций можно по итогам нескольких итераций предвидеть их дальнейший ход и за счет этого ускорить сходимость. Такой алгоритм существует и применяется в комплексе «СВАРКА».

Пошаговое моделирование сложного процесса. Число шагов за­висит от особенностей модели и требований, предъявляемых к результа­там. При явной схеме решения шаг ограничен условием устойчивости решения и зависит от размеров наименьшего элемента модели (см. рис. 2.7). При более крупном шаге получается решение, не имеющее ничего обще­го с реальным процессом.

При неявной схеме, если все процессы обратимые (не было текучести и разрушения) и ну жен только окончательный результат, всегда достаточно одного шага. Если происходят необратимые явления, влияющие на итого­вый результат, или представляют интерес промежуточные состояния, необ­ходимо разбивать процесс на шаги. Иногда эти шаги столь же мелкие, как и при явной схеме, поскольку точность обеих схем имеет одинаковый поря­док. С учетом итераций на каждом шаге время счета может оказаться очень большим. Если нелинейность процесса невелика, то можно отказаться от составления системы и прямой прогонки на каждом шаге, оставив матрицу жесткости постоянной. Это обычно не препятствует получению необходи­мой точности результатов, но увеличивает необходимое число итераций. На каждой итерации составляется только правая часть системы уравнений и осуществляется обратная прогонка, что требует гораздо меньшего времени. Однако при значительной нелинейности число итераций возрастает на­столько, что становится невыгодно использовать этот прием.

Передача данных между моделями процессов. Результаты модели­рования каждого процесса записываются в файлы. Это позволяет не только использовать их для моделирования другого процесса, но и просматривать, дополнительно обрабатывать для вывода на печать или хранения, продол­жать прерванное решение, начиная с любого из пройденных шагов.

Поскольку некоторые процессы требуют очень мелкого шага из усло­вия устойчивости, запись производится не после каждого шага, а с перио­дичностью, заданной в исходных данных. Граничные условия для таких процессов также задаются не для каждого шага, а сохраняются постоянны­ми в течение ряда шагов (стадии).

Элементы для разных процессов могут не совпадать, поэтому свя­зующим звеном являются узлы. Результаты моделирования приводятся к узлам и в таком виде передаются другому процессу, в котором при необхо­димости интерполяцией определяются значения для точек внутри элементов.

Расчленение громоздких моделей. Приемы экономии времени и па­мяти за счет разбиения сложной модели на подконструкции существуют, но в комплексе «СВАРКА» пока недостаточно развиты. Они обсуждаются применительно к другим комплексам в § 2.4.

Визуализация результатов решения необходима при анализе ре­зультатов, которые МКЭ выдает в таком количестве, что их иным способом невозможно воспринять, и помогает обнаружить ошибки, допущенные при построении модели.

При просмотре изображения плоской модели предусмотрены опера­ции показа номеров узлов, линий и элементов, поочередный или одновре­менный показ линий сетки элементов для различных процессов, а также из­менение масштаба. Номера линий контура облегчают ввод граничных уело-

вий, правильность которых может быть затем проверена по их условным | обозначениям на изображении модели.

< Для объемных моделей дополнительно необходимо удаление скрытых

линий и раскрашивание поверхностей, имитирующее их освещение источ­ником света, а также изображение в аксонометрии с выбором точки наблю­дения (ракурса) для лучшего представления о форме трехмерного объекта и сетке элементов на его поверхности на двумерном экране. Необходимо так­же изображение сечения по плоскости или по границе элементов для кон­троля внутренней сетки элементов.

При задании граничных условий целесообразно выделение участков внешней границы разными цветами.

При вводе таблиц свойств материалов правильность данных позволя­ют проверить изображения графиков функций. Это относится и к парамет­рам граничных условий, изменяющимся во времени.

Известны следующие средства изображения результатов решения МКЭ: скалярного или векторного поля для плоской детали, а также для на­ружной поверхности или поверхности сечения объемной детали.

Скалярный фактор может быть представлен изолиниями (разноцвет­ными или помеченными номерами), а также в виде аксонометрического изображения поверхности, для которой одной из координат является пред­ставляемый фактор. Эти средства позволяют изобразить поочередно отдель­ные компоненты векторного фактора. Кроме того, векторное поле на по­верхности можно представить в виде рассеянных по ней стрелок, длина ко­торых пропорциональна модулю вектора, а направление указывает линию максимального градиента. Можно также провести силовые линии (нормаль­ные к изолиниям), сгущающиеся в области высоких значений модуля. Под­ведение курсора к одному из изображенных на модели узлов позволяет за­просить информацию о значениях любых компонентов в этом узле. Поле перемещений узлов может быть представлено в виде искаженной сетки, по­казанной взамен или поверх исходной, причем масштаб искажений может отличаться от масштаба координат сетки. Изображение поля искажений можно совместить с изображением еще какого-нибудь параметра.

Если выбрать одну из линий на поверхности или в сечении детали, то 1 возможен одновременный просмотр сразу нескольких графиков функций

вдоль этой линии, ее проекции или развертки. Подведение курсора к точке на линии или на графике позволяет запросить текстовую дополнительную информацию.

Когда имеется несколько шагов решения, картину динамики его изме­нения могут дать либо серия графиков одной функции вдоль одной линии,

4 6705

либо графики функций для одной точки модели, аргументом которых явля­ется время или аналогичный ему параметр, либо мультфильм с чередовани­ем на экране изображений различных групп графиков.

Можно представить параметр в точках выбранной линии не в функ­ции координат, а в функции другого параметра.

Все эти средства реализованы или находятся в стадии реализации в комплексе «СВАРКА». Для управления ими используются нажатия кно­пок на панелях инструмента, движение мыши и нажатия ее кнопок в раз­личных частях обоих окон, а также нажатия клавиш клавиатуры. Для от­слеживания и изменения номера шага просматриваемых результатов в нижнем правом углу экрана появляется специальная панель, на которой по мере решения отображается число пройденных шагов. Пример резуль­татов показан на рис. 2.15.

Существующие программные комплексы МКЭ обычно содержат ряд обязательных звеньев, рассмотренных в этом параграфе. Наряду с этим ка­ждый из них ориентирован на определенный круг задач и включает допол­нительные возможности, актуальные для этих задач. Ряд таких более слож­ных проблем моделирования рассматривается далее на примере действую­щих программных комплексов.

Рис. 2.15. Результаты расчета температуры при наплавке на. железнодорожное колесо