Удельная работа деформации в элементарном объеме с координатами может быть вычислена как произведение интенсивности деформаций на интенсивность напряжений

. (3.102)

Удельная работа при холодной деформации значительно больше, чем при горячей. Это связано с более высокими значениями предела текучести при холодной деформации.

Неоднородность деформации по объему заготовки вызывает и неоднородность интенсивности напряжений, которую также нельзя считать постоянной по всему деформированному объему. Вследствие изменения деформаций и напряжений удельная работа деформации также существенно изменяется по сечению проволоки (или прутка). Наименьшие значения удельной работы соответствуют материалу, расположенному вблизи оси, наибольшие – материалу, находящемуся вблизи поверхности. Так, например, при волочении углеродистой проволоки (C=0,9 %) удельная работа вблизи оси проволоки при деформации и пределе текучести 1500 МПа равна 300 МПа, а на поверхности при и пределе текучести 2000 МПа равна 1200 МПа, т. е. в 4 раза больше.

Для определения мощности, усилий и температуры деформирования необходимо вычислить среднюю удельную работу :

(3.103)

Таким образом, средняя удельная работа при волочении зависит и от изменяющейся интенсивности деформаций, и от изменяющейся по объему интенсивности напряжений.

Подставляя формулы (3.97) и (3.88) в (3.103), получим:

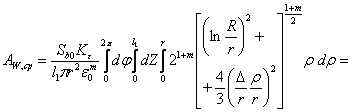
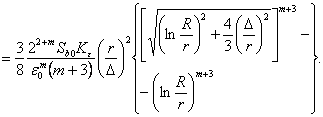(3.104)

Или

(3.105)

Мощность деформирования при волочении определим как произведение средней удельной работы на объем металла, проходящий через очаг деформации за единицу времени:

(3.106)

Здесь удельная работа в МПа, радиус – в Мм, скорость волочения в М/с.

Кроме деформирования, часть мощности необходимо затрачивать на преодоление сил трения, возникающих в деформирующем конусе и на цилиндрическом калибрующем участке (рис. 3.39).

На цилиндрическом калибрующем участке сила трения равна:

, (3.107)

Подставляя в формулу (3.107) вместо площади поверхности цилиндрического пояска площадь поверхности усеченного конуса (рис. 3.40), получим:

(3.108)

Где – максимальный предел текучести на поверхности

Проволоки с учетом упрочнения, в МПа, D – диаметр проволоки,

H – длина калибрующего пояска, в Мм, M – коэффициент трения.

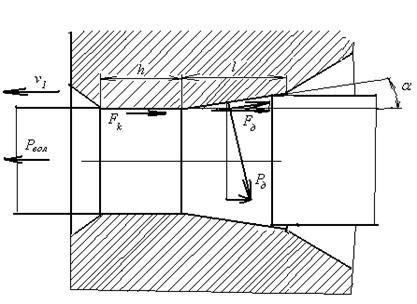
Рис. 3.39. Схема сил, действующих на проволоку в фильере

При волочении

Мощность, затрачиваемая на преодоление трения, будет:

. (3.109)

Суммарная эффективная мощность, необходимая на преодоление трения и деформацию равна:

(3.110)

Силу волочения вычислим как отношение мощности деформирования к скорости волочения, то есть

(3.111)

Для практических расчетов возможно применение упрощенных формул, например:

, (3.112)

Где – средняя величина предела текучести материала.

Из условий отсутствия пластических деформаций изделия вне очага деформации и прочности проволоки (или прутка, трубы) сила волочения не должна создавать в проволоке нормальных напряжений, близких к пределу текучести деформированного металла

. (3.113)