Прочность бетона при сжатии зависит при данной ак­тивности цемента от механических и деформативных свойств цементного камня и заполнителя, концентрации их в единице объема материала, прочности сцепления, а также от формы и крупности зерен заполнителя. Проч­ность бетона на плотных заполнителях принято выра­жать как функцию от активности цемента и водоцемент - ного отношения без учета влияния крупности зерен заполнителя его прочности и упругих свойств. Правомер­ность такой взаимосвязи многократно подтверждена экс­периментами. Между тем попытки описать прочность бетонов на пористых заполнителях (легких бетонов) ана­логичными зависимостями оказались безуспешными, а поэтому для каждого вида заполнителя подбирают корреляционные зависимости, по которым с различной степенью точности рассчитывают предполагаемую проч­ность легкого бетона. Если на прочность обычного бето­на влияет, как уже отмечено, ограниченное число факто­ров, то прочность легких бетонов определяется всеми пе­речисленными выше характеристиками его составляю­щих.

Если исходить из термодинамической теории прочно­сти твердых тел, основанной на феноменологических представлениях, то экспериментальные значения тепло­ты плавления и временное сопротивление при хрупком разрыве монокристаллов являются величинами одного порядка. В связи с этим можно предположить, что изме­нение энергетического состояния бетона под влиянием нагрузки зависит от упругой энергии W (аккумулиро­ванной в элементарных объемах), расходуемой на об­разование новых поверхностей в процессе разрушения материала [24].

Если а — напряжение, возникающее при внешней сжимающей нагрузке, a R& — предел прочности бетона, то можно записать:

W= Odo (11.15)

О

И после взятия интеграла

W = Rl/2. (11.16)

Внутренняя энергия материала может изменяться при передаче ему некоторого количества тепла AQ; при от­сутствии объемной деформации будем иметь

DW = AQ.

Величина AQ связана с энтропией материала 5Э со­отношением

A Q

DS9=-F-. . (11.17)

Таким образом, в первом приближении можно счи­тать, что прочность материала связана с энергетическим состоянием его структуры и энтропией. Полагая, что на системы стохастического (случайного) сложения, состоя­щие из большого числа элементов, можно распростра­нять понятия статистической физики, и приняв, что ве­роятность изменения энергетического микросостояния (прочности) системы W пропорциональна ее энтропии, можем написать:

DW

— = anvkadS0, (11.18)

Где Ctnp и — коэффициенты пропорциональности.

Если рассматривать бетон на макроуровне как двухком - понентный материал с объемными концентрациями раст­ворной части (матрицы) Vpc и включений VK3, тогда при постоянных объеме и температуре изменение энтропии бетона можно выразить в следующем виде:

DS^df-------------- ^------------- V (11.20)

Wpc + ^КЗ J

Где Скз и Срс—удельные теплоемкости включений и матрицы соот­ветственно.

Предполагая,

Что Скз^Срс и —получим:

DS3TtdVpc. (11.21)

В таком случае изменения состояний бетонов при различных объемных концентрациях его составляющих определятся как

С DW С

J — =anp*3J dV рс. (11.22)

1

После взятия интеграла будем иметь

In WQ - In Wvc =- Anp K3 1/кз. (И.23)

Отсюда нетрудно перейти к прочности бетона, приняв

G 2

В расчет, согласно (11.16), что Wpс= и WQ=

In — - In - j - апр ^кз, (П. 24)

Или

D _ АпрH v

= е ~ 3 "кз. (11.25)

Яре

Разложив функцию (11.25) в ряд Тейлора и ограничив его двумя первыми членами, получим

(11.26)

ИЛИ

Яб= ; (11.27)

Согласно выражению (11.27), прочность при сжатии двухкомпонентного материала определяется прочностью матрицы, ослабленной нарушением ее сплошности вклю­чениями и внутренним полем напряжений, характеризуе­мым коэффициентам аПр и k3. Совокупность этих фак­торов способствует снижению прочности бетона. Учи­тывая сказанное, примем, что-^^-^2-, где ао и йСц со-

2

Ответственно коэффициенты, определяющие влияние структурной неоднородности матрицы и прочность ее сцепления с включениями.

Если аре и егкз — напряжения в растворной части и крупном заполнителе, то максимальные их величины не могут превосходить напряжения, возникающие в одном

Из компонентов бетона. Если Якз>Дрс И ЕКз>Ерс, то разрушение бетона при сжатии происходит в основном по растворной части, т. е. цементному камню, причем, как это было показано, трещины зарождаются на по­верхности раздела «цементный камень—заполнитель». При /?кз<Ярс и Екз^Ерс вследствие повышенных дефор - мативных свойств пористого заполнителя напряжения распределяются таким образом, что в процессе деформи­рования бетона большую часть нагрузки воспринимает раствор, в связи с чем его несущая способность исчерпы­вается при меньших предельных напряжениях, чем в бе­тоне на плотном заполнителе. Этим обусловливается разрушение легкого бетона как по раствору, так и запол­нителю.

На этом основании средние результирующие напря­жения можно выразить равенством:

Арсз = арс =Ь <*кз' (11.28)

Знак плюс относится к бетону на плотном заполните­ле (#кз>#рс, £,Кз>£рс), а знак минус —на пористом заполнителе (/?Кз^/?рС> ЕКз^ЕрС).

Коэффициент осо, характеризующий взаимовлияние деформации от внешней нагрузки матрицы и включений, может быть выражен отношением:

Ao = 8Min/Emax- (11.29)

Для бетона на пористом заполнителе emin= 0рсз ■ — р Ерс

TOC o "1-3" h z = gpc акз, или в предельном случае emm=- .

Ерс Rpc

Учитывая условие совместности деформаций, а именно:

^Рс = имеем В таком случае, соглас-

Ерс Екз Ерс

но 11.28, можно написать: арсз=ере(£рс—£,кз), отсюда

8Рс= ареэ— и в предельном случае epC3=#pc. Следо - Ерс—Екз

Вательно, emax= Rvc — • Подставляя значения 8min и Ерс—Екз

Вшах в (11.29) для бетона на пористом заполнителе, по­лучим

#кз ЕРс —Екз А0 = . (11.30)

Крс С, рс

Аналогичным образом определяем значения 8mm и вшах для бетона на плотном заполнителе и после подста­новки в (11.29) имеем

Е в;сЕ д • (11.8D-

При внесении в выражение (11.27) коэффициента ксц и соответствующих значений ао из (11.30) и (11.31), получим два уравнения прочности бетона:

Vpc

На плотном заполнителе при ЕКз>Ерс и #Кз>Ярс

----- f ЕГР (Ч-32)

#СП ^рс "г Акз ^рс "Т &КЗ

На пористом заполнителе при ЕКз^ЕрС и RKs^RQc R6 = Rpc Г1 _ А. Укз Дре-Дк» Ере-Ек_3|_ ^

/гСц /<рс ьрс

Аналогичные формулы без множителя получены

Автором при несколько отличных от приведенного пред­посылках. &Сц находится в прямой зависимости от X це­ментного геля и в диапазоне от 0,876 до 1,65 изменяет­ся в пределах от 0,95 до 0,6 (рис 11.6, а).

Значения коэффициента k3 зависят от концентрации (насыщения) бетона крупным заполнителем и могут быть для каждого его состава определены по вели­чине К КЗ =Ущ£>щ+ УшРшГПщ= V' КЗ (1 +тщ).

Рассчитанные с помощью формул (11.32) и (11.33) к по результатам испытания образцов бетона на плотном и пористом заполнителях различного состава и экспери­ментально определенным величинам Ерс, Екз и i? pc, RKsf Значения K3 приведены; на рис. 11.6,6.

Из анализа формулы (11.32) следует, что при Екз> >Ерс и RK3>RVz крупный заполнитель оказывается не­догруженным, в связи с чем прочность бетона опреде­ляется в основном прочностью цементного камня. В са­мом деле, если г^кз—^-оо и акз то прочность бетона i?6-W? pc. Этим можно объяснить общеизвестный факт, что прочность обычного бетона выражается формулами, в которых не фигурируют свойства заполнителей, т. е. они выражают, по существу, прочность цементного кам­ня при данной активности цемента и В/Ц. Сказанное можно иллюстрировать данными (рис. 11.7), характери­зующими влияние состава заполнителей, расхода цемен­та и воды на прочность бетона [4]. На левой ветви кри-

 

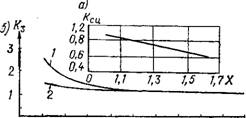Рис. 11.6. Значения коэффициентов 6Сц (а) и K3 (б) I — для пористого за­полнителя; 2 — для плотного заполните­Ля

 

/ о,$ 0,8 0,7 0,6 0,5 о, ъо, г 0,1 о

 

Вой при неизменном объеме крупного заполнителя проч­ность бетона снижается с увеличением количества песка, а затем по мере раздвижки раствором зерен щебня (правая ветвь) наблюдается закономерный рост проч­ности. При этом нетрудно установить, что прочность це­ментного камня составляет — 130%, а прочность раство­рных образцов—120% прочности бетона.

Величины прочности бетона при Х= и различных его составах, определенных экспериментально, могут быть с достаточной степенью точности воспроизведены расчетным путем по формуле (11.32). В этой связи рас­смотрим три характерные точки на кривых прочности бетона (рис. 11.7), а именно: две на левой ветви при за­полнении цементным камнем и раствором пространства между зернами щебня и одну на правой ветви кривой при раздвижке их раствором. Для первой и второй точек имеем: VK3=L-0,67+0,67-0,33~0,9; /г3=2,5 и /гсц=0,95 при исходных данных: RK=70 МПа; /?кз=150 МПа; Ек= 1,9-104 МПа и Екз=5,5-104 МПа. Тогда по форму­ле (11.32) для первой точки получим

Г 2,5 70 1,9

/?б = 70 1 --^^-0,9;

= 57 МПа.

0,95 70+ 150 1,9 + 5,5

Для второй точки при заполнении пустот в щебне ра­створом: fe3=2,5; /гсц=0,95; ЯРс = 60 МПа; Ерс = 3,5Х ХЮ4 МПа:

Яб = 60

2,5 од 60 3,5

= 45 МПа.

0,95 60+ 150 3,5 + 5,5

0,532

55 МПа.

1 ■

0,95

Для третьей точки при 1/щ=0,6; Укз=0,6-0,67+0,6Х Х0,67-0,33=0,532 по рис. 11.6,6, &3=1,2, следовательно: 1,2 Л _ 60 3,5

Яб = 60

60+ 150 3,5 + 5,5

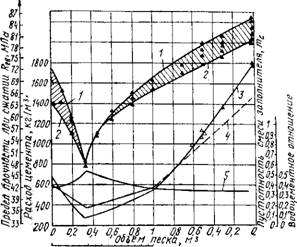
7 1 08 06 0,2 О Объем Щебням* Рис. 11.7. Зависимость прочности бетона от его состава

 

1 и 2 — кривые прочности (между ними область разброса прочности); 3 — кри­вая расхода цемента в кг на 1 м3 бетона; 4—кривая пустотности смеси за­полнителей; 5 — кривая

Сравнение вычисленных значений RQ С данными рис. 11.7 показывает, что они хорошо согласуются друг с другом. Можно убедиться в том, что для правой кривой результа­ты, получаемые по формуле (11.32), близко совпадают с вычисленными значениями, по формуле прочности бе­тона, приведенной в работе [4].

В отличие от плотных, пористые заполнители снижа­ют прочность бетона и тем значительнее, чем больше от­личаются Екз и RK3 от ЕрС и /?рс, поэтому в формулы ви­да R6=F(RnB/U,) необходимо ввести дополнительный па­раметр Сл, равный множителю в скобках формулы (11.33), и вместо (В/Ц) ост —истинное его значение, т. е. (В/Ц) оГст.

 

Из формулы (11.33) следует, что при Е3=Е1)С или /?кз=/?рс Сл=1 и прочность бетона определяется проч­ностью раствора, на котором он приготовлен. Этот ча­стный случай вполне реален, так как истинная проч­ность пористых заполнителей в бетоне значительно вы­ше, чем при испытании дроблением. Объясняется это тем, что при определенном напряженном состоянии, из - за малых деформаций раствора, заполнитель испытывает объемное обжатие, в связи с чем воспринимает нагрузку без образования трещин. Однако вследствие неодинако­вых прочностных и деформативных свойств составляю­щих происходит перераспределение напряжений, сопро­вождающееся большим ослаблением материала запол­нителя, чем раствора. При лавинном трещинообразова - нии в заполнителе напряжение воспринимается пол­ностью раствором и только с этого момента вплоть до разрушения бетон работает как материал, ослабленный пустотами. С увеличением прочности раствора, создаю­щего эффект обоймы, условия, при которых заполнитель играет в бетоне роль «пустот», наступают при больших сжимающих внешних нагрузках.

Здесь уместно отметить, что при подстановке в фор­мулу (11.32) Em=Evc и Rk3=Rvc Мы не получаем равен­ства RQ=Rc, так как крупный заполнитель из плотных горных пород не может иметь свойства, близкие к свой­ствам цементного камня или раствора при обычных спо­собах уплотнения бетонной смеси. Исключение состав­ляет вибропрессованный бетон; в этом случае может оказаться, что Rvc^Rm и Ерс^ЕКз, в связи с чем проч­ность бетона следует вычислять как для легкого бетона по формуле (11.33).

В отличие от других формул, аналогичных в некото­рых отношениях формулам (11.32) и (11.33), в послед­ние входят не отношения RKs/R^C Или ЕКз/ЕрС, а их про­изведения, при этом Екз и RK3 в зависимости от влияния их на прочность бетона представлены в виде выражений: (Ерс+Екз), (Ярс+#кз) и (Ерс—Екз), (#рс—#кз), т. е. как бы результирующих модулей упругости и прочно - стей составляющих двухкомпонентной системы. Проч­ность бетонов на плотных и пористых заполнителях нельзя к тому же выразить единой зависимостью, по­скольку характер эпюр раецределения средних на­пряжений в обоих случаях различен [65]. Форму­лы (11.32) и (11.33) достаточно хорошо. выражают зависимость прочности бетона не только от механи­ческих и деформативных свойств составляющих, но и от водоцементного отношения. При различных значениях Ки. т и неизменной активности цемента Rn Влияние остаточного водосодержания в смеси на проч-

R6} МПа

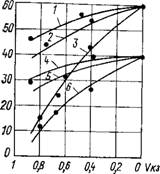
Рис. 11.8. Изменения прочно­сти бетона на плотном (1, 4) И пористом (2, 3 и 5, 6) запол­нителях в зависимости от рас­хода цемента и способа уплот­нения; 1У 2, 3 и 4, 5, 6 при уплотнении вибрированием с частотами 150 и 50 Гц соот­ветственно

Ность обычного и легкого бетонов описывается семейст­вом параллельных кривых.

433

Для оценки степени совпадения вычисленных по фор­мулам (11.32 и (11.33) значений прочности с резуль­татами испытания при сжатии образцов бетона на гра­нитном щебне (ЕКз=5,5-104 МПа; RK3=150 МПа), вул­каническом туфе (ЕКЗ= 5,5-104 МПа; RK3=30 МПа) и шлаке (Екз=0,4-104 МПа; RK3=7 МПа) при Ерс=3,5Х ХЮ4 МПа, /?рс=40 и 60 МПа на рис. 11.8 приведены данные, характеризующие изменение прочности бетонов в зависимости от относительного содержания в нем круп­ного заполнителя, что адекватно расходу цемента. Кри­вые показывают, что чем слабее щебень, тем значитель­нее возрастает прочность бетона с увеличением расхода цемента (прочность бетона на гранитном щебне изменя­ется с увеличением расхода цемента несущественно), однако отсюда еще не следует, что эта мера является радикальной для достижения высокой прочности легко­го бетона. Не говоря уже об экономике, расход цемента, превышающий оптимальный, снижает трещиностойкость и повышает деформации от усадки и ползучести. Как это следует из рис. 11.8, в целях повышения прочности бетонов предпочтительнее высокоактивные портландце - менты и эффективные способы приготовления и уплотне­ния смесей с минимальным водосодержанием, позво­ляющие максимально использовать потенциальные свой­ства вяжущих. Так, например, при одном и том же рас­ходе цемента независимо от вида крупного заполнителя

28—634

Прочность бетона при X— 1 возрастает примерно в 1,4— 1,45 раза.