Предварительный анализ длинных, свободно лежащих на опорах по периметру панелей из сложных композиционных материалов структуры (0°, 90°, ±45°), может быть проведен с ис­ пользованием кривых, представленных на рис. 20.16.

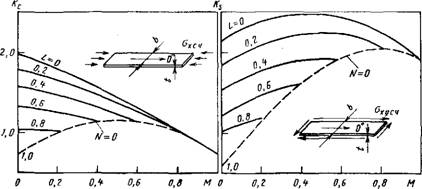
А) ' б)

Рис. 20.! 6. Напряжения продольного изгиба в длинных, свободно опертых по периметру плоских пластинах:

А - прн сжатии (а - EJBU - 0.1; Х - О,,/*,,=0.375): <тхсг =. „„,,/(1 + 1.2 <»,„/<?„) [см - (20.36)]; axc, r ~ КсЕи где Кс - (я/6)1 {(Л„Лгг)1/2 + + 2AJ їси.

<20.28) при сдииге (о - Яи/Яи = 0.1; К == QJEa = 0.375): аху„ = ахуегП +

+ 0,395(/;11/Й1>) (і/b)*і їси. (20.41)1; а'ху„ = (t/b)%: Ks из (20.31); М - доля слоев

В ориентацией 90°; l — доля слоев с ориентацией 0е; n — доля слоев с ориентацией ±45°

12 5 10 20 50 100 ы„/ь, мпа

Рис. 20.17. Оптимальные напряжения сжатия в длинных, свободно опертых по периметру плоских пластинах слоистых пластиков:

Nx/b — структурный индекс; t—Mx/o с max; "стах — максимальное напряжение сжатия: 1 — ЭБП марки avco 5505; 2 — ЭУП марки t300/ns208', 3 — ЭУП марки •4S-1/3501-5.4; 4 — ЭУП марки oy 70/hye 1534; 5 — «Кевлар-49»/С£ 3305

Эти кривые были построены исходя из предположения о том, что панели из композитов однородны и обладают ортотропией. Для их построения были использованы уравнения (20.28) для

Осевого сжатия и (20.31) о о,2 B, f ju; _ о,8 i, o л для сдвига в плоскости слоя,

В которые были включены значения Аи, полученные из уравнения (20.7). Кривые строились с использованием значений а — Е22/Еи = 0,1 и К = G12/Ј22 = 0,375, ко­торые являются достаточно типичными для композитов ЭБП и ЭУП при комнатной температуре (см. рис. 20.8).

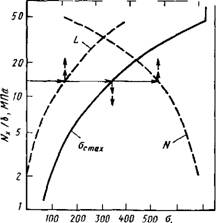
,МПа

Рис. 20.18. Определение оптимальной структуры выкладки для обеспечения свойств панелей нз слоистых композитов при сжатии ЭУП марки >4S-l/3501-5i4:

Р — оптимальная доля слоев; l — доля слоев с ориентацией 0°; n — доля слоев с ориента­цией dz45°; Nx/b — структурный индекс; °с max — максимальное напряжение сжатия

Оценка свойств панелей из КМ при сжатии может быть проведена с исполь­зованием кривых, представ­ленных на рис. 20.17 и 20.18. На рис. 20.17 показано из­менение оптимальных на­пряжений сжатия в зависи­мости от структурного ин­декса. Все кривые построе­ны для ламинатов, в кото­рых слои с ориентацией 90°

200

100

50

20

0,1 0,2 0,5 1,0 2 5 10

Рис. 20.19. Определение оптимальных напряжений сдвига в длинных плоских

Образцах, свободно опертых по периметру:

Nx jb — структурный индекс; о шах — максимальные напряжения сдвига; 1 —> ЭБП марки avco 5505; 2 — ЭУП марки 7"300/./V5208; 3 — ЭУП марки Л5-1/3501-5Л; і ~ ЭУП марки oy 470/hye 1534; 5 — «Кевлар-49»/СЯ 3305

Отсутствуют, т. е. М = 0. Однако следует заметить, что опти­мальные напряжения изменяются несущественно вплоть до зна­чений М < 0,2. На рис. 20.18 показано, при каких структурах выкладки композита ЭУП типа AS-13501-5A могут быть дости­гнуты максимальные напряжения.

Кривые на рис. 20.17 и 20.18 построены с учетом исключе­ния эффектов, связанных со сдвиговой жесткостью при межосе­вом сдвиге, и исходя из соотношений:

Где Кс — коэффициент напряжения продольного изгиба при сжатии; Nx — осевая нагрузка сжатия; b — ширина панели; t — толщина панели. Для конструкций, в которых необходимо избегать продольного изгиба, максимальные (или оптимальные) напряжения (Тс max определяются из равенства охсг — ах. Тогда

Или

(20.44)

Значения Кс, взятые из рис. 20.16, совместно со значениями ах из уравнения (20.14) и данными по свойствам материалов из табл. 20.6 позволили получить кривые для рис. 20.17 и 20.18.

Те же приближения были использованы для получения кривых на рис. 20.19, построенных для определения оптимальных сдвиго­вых напряжений в длинных и плоских панелях. Для условий этого нагружения уравнение (20.44) преобразуется в

(20.45)

Где Nxy — приложенная к образцу сдвиговая нагрузка. Напря­жение сдвига оценивается равным 0,25GZ, что является практи­чески минимальным уровнем напряжений для сдвиговых дефор­маций в панелях композитов. Оптимальная структура выкладки в панелях составляет по 50 % для слоев с ориентацией 90J и ±45°, что соответствует максимальному коэффициенту напряже­ний при продольном изгибе (см. рис. 20.16).

СПИСОК ЛИТЕРАТУРЫ

Barmink Е., Hadcock R. and Forsch Н., «Advanced Design Composite Aircraft

Study», Paper No. 77-393, presented at the 18th AIAA/ASME Structures, Struc­tural Dynamics and Materials Conference, San Diego, California, March 1977.

Hadcock R., «The Application of Advanced Composites to Military Aircraft», 1CAS Paper No. 76-09, presented at the 10th Congress of the International Council of the Aeronautical Sciences, Ottawa, Canada, October 1976.

Schwartz P., «Advanced Design Composite Aircraft, the Next Step for Compo­sites», SAWE Paper No. 1105, Index Category No. 27., presented at the 35th Annual Conference of the Society of Allied Weight Engineers, Philadelphia, Pennsylvania, May 197G.

Ludwig W., Erbacher H. and Lubin G., «Composite Horizontal Stabilizer for the B-l: Design, Fabrication and Test», 32nd Annual Technical Conference; Reinforced Plastics/Composites Institute, SPI, Section 15B, Washington, D. C., February 1977.

6. Tsai S. W. and Pagano N. j., «Invariant Properties of Composite Materials», Composite Materials Workshop, Technomic, January 1968.

Suarez J. A., Whiteside J. B. and Hadcock R. N., «The Influence of Local Failure Modes on the Compressive Strength of Boron/Epoxy Composites», ASTM Special Technical Publication 497, 1972.

Department of Defense, «Structural Sandwich Composites», MIL-HDBK-23A, Washington, D. C., June 1968.

Timoshenko S. P. and Gere J. M., Theory of Elastic Stability, Second Edition, McGraw-Hill, New York, 1961.

Plantema F. J., Sandwich Construction, John Wiley Sons, New York, 1966.