1. О методике исследования устройств с самосинхронизирую- щимися дебалансными вибровозбудителями. Из изложенного вы­текает следующая методика исследования конкретных вибраци­онных устройств с самосинхронизирующимиея вибровозбудите­лями [25]).

1) Находят установившиеся вынужденные Т = 2зт/(о-периоди-

ческие колебания

»

и = и° (erf, ак) (10.1)

несущего тела или несущей системы тел под действием вынуж­дающих сил, развиваемых вибровозбудителями при равномерном вращении роторов с некоторыми произвольными начальными фа­зами «і, .. ак, т. е. при вращении роторов по закону

ф* = ф° = os (erf + as). (Ю.2)

Особенно просто такие колебания находятся в случае линейной несущей системы.

, 2) Составляют основные уравнения (уравнения типа (8.4), (8.28), (8.29), (8.36), (8.37) и т. п.) для определения постоянных а, в возможных синхронных движениях. Это может быть сделано одним из трех способов.

а) Непосредственное усреднение дифференциальных уравне­ний движения роторов еиброеозбудителей. Составляют уравне­ния движения роторов вибровозбудителей с учетом подвижности несущей системы; эти уравнения записывают в форме

+ К (ф, — csc>) = Ф* (<plt..., фй, и, и, и, ш) (10.3) (* = 1,

линеаризовав выражения для моментов L3, передаваемых от дви­гателей, и моментов сил сопротивления R, вблизи синхронной угловой скорости согласно равенствам (4.10), (4.11), (4.13). Пос­ле этого правые части уравнений (10.3) усредняют за период Т = 2л/ш в предположении, что величины ф* и и изменяются по законам (10.1), (10.2), и получают основные уравнения в виде

Ps(ai, ...,а*)®£<(ф;)>э

353 <Ф* (ф?, • • •, ф“, и0, и0, и0, <of)> (s = 1, ..., к). (10.4)

Этот способ является наиболее универсальным; он, в частности, пригоден и в случае, когда среди вибровозбудителей имеются планетарные. Однако в отличие от двух других способов он тре­бует составления не только уравнений вынужденных колебаний тел несущей системы, но и уравнений движения вибровозбуди­телей с учетом подвижности несущих тел.

б) Использование выражений (8.7) для потенциальных м-омен - тоє $ через усредненную функцию Лагранжа системы или при­менение интегрального критерия устойчивости (.экстремального свойства) синхронных движений. При этом способе составляют выражения для потенциальной и кинетической энергий всей си­стемы Пи Т (или же для потенциальной и кинетической энергии системы связи По и То), после чего образуют функцию Лагранжа L — T — П (или Ь0 — Т0 — По). Затем производят усреднение этой функции за период при значениях <ps = <р° ив = в°, определяе­мых формулами (10.1), (10.2). Получающуюся функцию А (или Ло) используют для определения моментов JK, = —дК/да, ==■ = ~дАо/даг, входящих в основные уравнения (8.4), или же, в. случае существования йотенциала усредненных неконсерватив­ных сил В (см. п. 4 § 8), для составления потенциальной функции D = —(Л + В) (илк D = —(Ло + 5), см. равенство (8.50)) и после­дующего применения интегрального критерия устойчивости. Ос­новные уравнения получаются в этом случае из условий стацио­нарности dD/das = 0 функции D. Если силы трения в несущей системе в первом приближении не учитываются, то потенциал усредненных неконсервативных сил В непременно существует, причем

я = 2 [a*Lt (osw) — R°s (ю)] as. (10.5)

s=l

Если, кроме того, несущая система является в первом при­ближении линейной, то вместо функции Лагранжа всей системы можно вычислять лишь функцию Лагранжа несущей системы Lm = Tm - П(1) и величину А(1) = <(£/>)>. При этом согласно <8.51) jD==A(I> — В, а вибрационные моменты = дЛ(1)/да,

(см. равенства (8.35)).

в) Использование выражений для вибрационных моментов через гармонические коэффициенты влияния. Этот способ, при­годный в случае квазилинейной несущей системы, подробно опи­сан в п. 3 § 8. Его использование требует лишь составления и решения линейных дифференциальных уравнений, описывающих в первом приближении колебания несущей системы тел под дей­ствием гармонических сил, приложенных к осям вибровозбуди­телей. Подчеркнем, что этот способ в принципе пригоден в слу­чае любых вибровозбудителей и в случае, когда учитываются силы сопротивления при колебаниях несущей системы.

3) Из основных уравнений Р, = 0 определяются значения разностей фаз as — ak в возможных синхронных движениях воз­будителей и исходное приближение к синхронной угловой ско­рости со; впрочем, последняя может быть найдспа непосредствен­но по формуле (5.18). Условия существования вещественных решений основных уравнений относительно as — ah и являются условиями возможности самосинхронизации вибровозбудителей.

4) Из числа найденных решений основных уравнений отби­рают те фазировки, которым соответствуют устойчивые СИНхрОН-

fi И. И. Блехман ные движения. Этот отбор производят либо на основе алгебраи­ческого уравнения (8.31), все корни которого для устойчивой фазировки должны иметь отрицательные вещественные части, либо на основе интегрального критерия устойчивости, согласно которому устойчивые фазировки соответствуют грубому миниму­му потенциальной функции D.

5) Отобранные значения фаз се, —се[26] подставляют в выраже­ние для а0 и тем самым находят в первом приближении закон колебаний несущей системы тел в устойчивых синхронных дви­жениях.

6) Если устойчива фазировка возбудителей, при которой реа­лизуется требуемый закон колебаний несущей системы, то про­изводят проверку стабильности согласно изложенному в § 9. В случае, когда требуемая фазировка неустойчива, пытаются обеспечить ее устойчивость либо одним из способов, указанных в § 11, либо путем применения средств принудительной синхро­низации (см. там же). В случае, если требуемая фазировка устой­чива, по не достаточно стабильна, изменяют параметры колеба­ний или структуру несущей системы.

2. Примеры исследования самосинхронизации внбровозбудителеи. Про­иллюстрируем изложенное на нескольких простых примерах; более сложные примеры можно найти в книге [57].

Пример 1. Самосинхронизация дебалансных возбудителей в простей­шей колебательной системе. Рассмотрим случай, когда несущее тело имеет всего одну степень свободы (рис. 6). Поскольку способы а) и б) составле­ния основных уравнений по существу иллюстрируются содержанием §§ 4 и 7, то здесь остается составить выражение для вибрационного момента через гармонические коэффициенты влияния. Очевидно, что в рас­сматриваемом простейшем случае все коэффициенты, кроме равны

пулю. а колффицпепты К'^и одинаковы для всех s и т. е. можно по­ложить = Кии. Величина Кии определится в результате решения уравнения

Мх + схх = sin cot, (10.6)

описывающего колебания платформы под действием гармонической вынуж­дающей силы единичной амплитуды, направленной вдоль оси Oiu. Получаем

что упругие опоры являются весьма мягкими, т. е. что частоты свободных колебаний тела Вв па опорах значительно меньше угловой скорости син- хронного вращения роторов со. При этом потенциальной энергией 11 и ответствующими членами в уравнениях движения тела В о можно прене­бречь. Тогда при вращении роторов по вакову (10.2) колебания тела Вй будут описываться уравнениями

	U, и
4	г	М,1 - г А
	О	0.1 °2	X, и

, C0~0

C0~0. Рис. 15.

Ых0 = F[cos (со* + tti) + cos (cot + Иг)], щч = — #[01 sin (cot + «О -f

+ ог sin (cat + a2)], (Ю.7)

/фЬ = Frt[oi sin (cot + Ki) —

— 02 Sin (tOi + Cfc)],

где M и / — соответственно масса и момент инерции вспомогательного те­ла (см. п. 5 § 8), а F = тгto2 — амплитуда вынуждающей силы, развива­емой каждым возбудителем. Решением уравнений (10.7), соответствующим

установившимся вынуждеттым колебаниям, будет

F

1^2 lC0S (®* + «і) + (C0S «* + «2)1’

F

(10.8)

Ф° =

l°isin (ш + ai) + ^ sin (соt + a2)], Fr

—j [oL sin (соt + ax) - o2 sin (cot + oa)].

Для составления основных уравпеппй воспользуемся интегральным критерием устойчивости. Поскольку парциальные скорости возбудителей предполагаются одинаковыми ц положительными, то роль потенцпальной функции в данном случае будет играть среднее значение функции Лагран­жа вспомогательного тела, равное ввиду предположения о мягкости упру­гих опор просто среднему значению кинетической энергии этого тела. Про­изводя усреднение при учете выражений (10.8) и равенств (4.17) легко получим

D _ л<1) = <(?(!))> = ± (М [(і0)2 + (у0)2] + I (ф°)2> =

F2 (. . Мг*

= Ш^і + а^-Сіа2~Т-)соЧа2-аі)+Сі. (10.9)

Здесь С, — не зависящая от углов а, и а2 величина. Как и следовало ожи­дать, функция D в данном случае зависит только от разности фаз а —

= 0.2 — И]. Приравнивая пулю производную ЗД/Sa, приходим к следующему основному уравнению для определения разности фаз а в возможных син­хронных движениях:

(10.10)

sin а = 0.

Это уравнение имеет два существенно различных решения

(а}. = (о.* -

= 0

(iu. il)

/„% /„ і IVV12 «СС2 —- lit} о — я,

первое из которых назовем синфазным, а второе — противофазным. При вы­полнении условия

Mr2

1 + <Tj02 — СЛ —J— <0 (10.12)

функция D при а = (а), = 0 имеет минимум, а при а — (а)2 = я — мак­симум, и поэтому, в соответствии с интегральным критерием устойчивости, синфазное движение является устойчивым, а противофазное — неустой­чивым.

Пусть сначала роторы возбудителей вращаются в одинаковых направ­лениях, т. е. С1С2— 1. Тогда при выполнении условия

Mr1!! > 2 (10.13)

устойчивым будет синфазное вращение роторов, обеспечивающее, как не­трудно видеть из равенств (10.8), круговые поступательные колебания

= Мгг/1>2 Mr/l<2

s)

Рис. 16.

тела Во с амплитудой г0 — 2me/М (рис. 16, а). При выполнении противопо­ложного неравенства Mr2II < 2, напротив, устойчивым будет противофаз­ное вращение роторов, приводящее к поворотным колебаниям тела В0 с уг­ловой амплитудой ф0= 2тегЦ (рис. 16, б).

При вращении роторов в противоположных направлениях, когда а1о2== = — 1, условие (10.12) нигода не выполняется, и поэтому всегда устойчи­во противофазное вращение, приводящее, как нетрудно убедиться с по­мощью (10.8), к прямолинейным поступательным гармоническим колеба­ниям тела В0 перпепдикулярно плоскости, в которой лежат оси вращения роторов (рис. 16, е). Амплитуда указанных колебаний Л0~ 2те/М.

Приведем выражение для вибрационных моментов, знание модуля ко­торых, как отмечалось в § 9, необходимо при оценке стабильности:

W{K) _ _ W(.K) = і ~ 2 да.

F2 ( Mr2

■^Г [1 + а1а2 - aXff2 - f-J Sin “• <10Л4>

Те же результаты, как нетрудно убедиться, получаются при использова­нии гармонических коэффициентов влияния.

Установленные здесь закономерности самосинхронизации двух вибро­возбудителей в описанной простой системе находят широкое применение в вибрационных машинах и устройствах (см. § 15).

3. Сводка условий устойчивости важнейших синхронных дви­жений вибровозбудителей в некоторых колебательных системах. В табл. 2 приведены условия устойчивости важнейших режимов синхронного вращения роторов вибровозбудителей в некоторых практически интересных колебательных системах и выражения для модулей вибрационных моментов; описан характер колеба - инй несущих тел в соответствующих режимах; даны ссылки на источники, в которых система изучена с помощью различных ва­риантов изложенной выше методики.

Более полная таблица приводится в книге [57].

Дадим некоторые общие пояснения и примечания к таблице.

1) В случаях, когда это не оговаривается особо, предполага­ется, что привод возбудителей осуществляется от двигателей асинхронного типа, причем парциальные скорости всех возбуди­телей одинаковы и положительны.

2) Термин «мягко амортизированное твердое тело» означает, что частоты собственных колебаний тела на упругих опорах зна­чительно ниже наименьшей скорости вращения валов возбуди­телей о (на схемах соответствующие упругие элементы снабже­ны надписью с0 ~ 0).

3) В таблице приняты следующие общие обозначения: М, /*, /„, /г — масса и главные центральные моменты инерции относи­тельно соответствующих осей вспомогательных тел (т. е. тел, по­лучающихся из исходных, если сосредоточить массы всех деба­лансных и планетарных возбудителей в центрах вращения их векторов — эксцентриситетов, а массы всех возбудителей направ­ленного действия — в их средних положениях); О — центр тяже­сти вспомогательного тела; т, є — масса и эксцентриситет возбу­дителя; оо — ось вращения ротора возбудителя.

4) При наличии двойных знаков в формулах столбца 4 таб­лицы следует принимать либо только верхние, либо только ниж­ние знаки.

5) При отнесении реальной системы к одной из представлен­ных схем следует обращать особое внимание на правильность учета существенных степеней свободы несущих тел, ибо при

Условия устойчивости важнейших синхронных движений

Динамическая схема, обозначения

Краткое описание системы. Разделы книги или публикации, в которых рассмотрена система

Произвольное число одинако­вых дебалансных вибровозбудите­лей, установленных на абсолютно твердом теле с одной степенью свободы.

См. §§ 4—7 гл. ?, а также [31, 57]

Примечания: 1. Результат справедлив и для возбудителей направленного асронные движения.

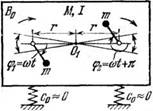
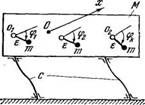
Два одинаковых дебалансных вибровозбудителя, симметрично установленные на мягко аморти­зированном твердом теле, которое может совершать плоские колеба­ния; оси возбудителей параллель­ны, лежат в одной плоскости с центром тяжести тела О и удале­ны от него на одинаковые расстоя­ния г.

См. п. 2 § 10 гл. 3, а также [36, 57]

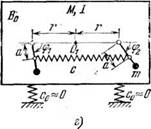
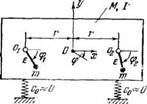
Та же система, что и в п. 2, но роторы возбудителей связаны пру­жиной жесткости с, присоединен­ной на расстояниях а от осей ро­торов.

См. § 11 гл. 3, а также [57]

Таблица 2 возбудителей в~некоторых колебательных системах Характер синхронного движения (в пер­вом приближении) Условия устойчивос­ти синхронного дви­жения Выражения для мо­дулей вибрационных моментов W(co) возбудителей несущих тел а) Іфі1=1ф21=- —=ІфлІ=ші Гармонические поступательные колебания CD < р = Yс/М (р — частота сво­бодных колеба­ний системы) Для к=2 ^(Ю)=-|-Х т2Є2ш4 1 I Х Af р2 — со2| гвовать и другие син- б) ІфіІ=Іф2І = — —=1фЬ/а1= = 1фй/2+1+Л| = — ...= |ф&+л|=ю* (к — четное) действия. 2. При чис. Отсутствие ко­лебаний те возбудителей k > 2 со > р — V с/М в системе могут сущес а) ф]=±юг, ф2=Ч=(ш(+л) (роторы возбуди­телей вращаются в противополож­ных направлени­ях) Прямолинейные поступательные гармонические колебания в на­правлении оси Оу с амплитудой А0=2тг/М Режим устой­чив при любых со­четаниях пара­метров, если гфО Й? (0J) = 1 т2е2ша Mr2 — 2 М I б) <Pz=±e>t (роторы возбуди­телей вращаются в одинаковых на­правлениях) Круговые по­ступательные ко­лебания с ампли­тудой г0~2тв/М Mr* / >2 = 1 т*е*с)3 _ 2 Л/ Х I Мгг х|-Г-2 в) ф!=±СOi, Фг=±(соі+п) (роторы возбуди­телей вращаются в одинаковых на­правлениях) Поворотные гармонические колебания с угло­вой амплитудой Ф0=2 тег/1 Mr2 / <2 а) То же, что в в п. 2, а Mr2 Мсаа I т2е2ы2 То же, что. и в п. 2, а б) То нее, что и в п, 2, б Mr2 Мсая —;—> 2— „ о „- То же, что и в пп. 2, б н 2, в в) То же. что н в д. 2, в Mr2 „ Мса2 I ^ ^ т2Ё2С02

.

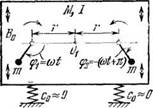
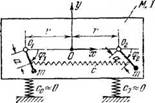
Та же система, что и в п. 2, но роторы либо связаны упругим или электрическим валом жесткости с, либо приводятся во вращение от одинаковых и одинаково установ­ленных синхронных двухполюс­ных электродвигателей с жестко­стью характеристики в рабочей точке dL*/dQ=—c.

У"

См. § 11 гл. 3, а также [57]

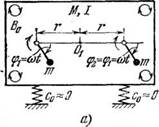
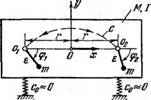
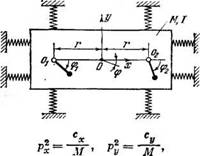
Та же система, что и в п. 2, но твердое тело связано с неподвиж­ным основанием симметричной системой упругих элементов с жесткостями Сх, Cyj =0).

«р м

См. [57, 79]

р*

= '

0)

Та же система, что и в п.12, но с твердым телом связана посред­ством упругих элементов жестко-

сти с и демпфирующих элементов с коэффициентом сопротивления Р дополнительная симметрично расположенная масса М2.

2 н» М1М2 р — м*' м — мг + м3

См. [56, 57]

2П :

м*

Примечание. О системах, в которых к телу Mi присоединены более сложные

Та же система, что и в п. 2, но оси роторов возбудителей не ле­жат в одной плоскости с центром тяжести тела О.

См. [38, 42, 57]

	№	Ґ’і
	-~JL	/ О?
		£v
	и	Л___ 777	3

Сд^О

Be г

- мі

Та же система, что и в п. 2, но возбудители не дебалансные, а мопогармонпческие возбудители направленного действия; Плинии действия вынуждающих сил ле­жат в одной плоскости с центром тяжести тела О и равноудалены от него.

См. [42, 57]

ЩШПШШ

4'Є І т-є

/77 2

V/У////

: Co~U

Табл. 2 (продолжение) Характер синхронного движения (в пер­вом приближении) Условия УСТОЙЧИВОС­ТИ синхронного дви­жения Выражения для мо­дулей вибрационных моментов ТУ(ш) вовбудителей несущих тел б) То же, что и в п. 2, б (кроме формул для амплитуд) Mr2 I >2- 2 (Л, а— 1) (А2 —1)2+4/г2* м2 х Mi (?ь= p/со, п1=п/со) W (<£>) = 1 m2e2co2 I Mr2 ~ 2 М 1 / + + 2(a*-ix в) То же, что и в п. 2, в (кроме формул для амплитуд) элементы, см. [56, 57]. Mr2 / <2~ 2 (А2 - 1) ~(А2-1)2 + 4п2Х мг х М1 Фі=±юг, q>2=:F(cof+iO (роторы возбуди - телей вращаются в противополож­ных направлени­ях) П рямо линейные поступательные гармонические ко­лебания. с ампли­тудой А 0~2тг1М, направленные вдоль оси Оу (пер­пендикулярно плоскости осей роторов OjOg) Реяшм устой­чив при любых сочетаниях пара­метров, если Гф 0 W (со) = 1 m2e2co2 Mr* ~ 2 М I а) q>t=dz(otf Ф2==ьсог Прямолинейные поступательные гармонические ко­лебания с ампли­тудой AQ=2m&/M, направленные вдоль оси Оу (пер­пендикулярно плоскости осей возбудителей) Mr2 / >4 ~ 1 т2е2со2 Лу-Х | Afr21 Х 11 J-1 б) ф2==Ь(<М+я) Поворотные г армоиические колебания с угло­вой амплитудой гп.=9т»г/Т 'i'U —••***••■* Мг°~ I <1

Краткое описание системы. Разделы книги или публикации, в которых рассмотрена система

п/п

Динамическая схема, обозначения

Два одинаковых дебалансных вибровозбудителя, установленных на одной из масс цепной двухмас­сной колебательной системы.

См. [57, 329]

Примечание. О более общих цепных системах с произвольным числом масс

10

Та же система, что и в п. 9, но массы могут перемещаться во вза­имно перпендикулярных направ­лениях и возбудители установле­ны на «внешней» массе.

См. [42, 57, 246, 330]

Табл. 8 (продолжение у

несущих тел

Характер синхронного движения (в пер­вом приближении)

возбудителей

Условия устойчивос­ти синхронного дви­жения

Выражения для мо­дулей вибрационных моментов WXra)

а) ІФіі=ІФ2і= = cot

1 т2е2 со*

W(CD):

■X

2 МЛ

р2 — со2 (р2 — со2) і

X

X

X

co2j

Гармонические колебания обеих масс

(р2 — со2)/(I’l — — СО2) (р2 — СО2) > >0, где p=cjM2, a Pi и р2 — корни уравнения -£і- 4. д- м2)^

м±мъ

= 0

+

б) |ф! І=

= |qyfn|=<»f

Отсутствие ко­лебаний (р2 — ®2) / (pi —

— со2) [pi — со2) <

<0

и произвольным числм любым образом размещенных возбудителей см. [57, 249, 329].

м_ м.

X

АІ.— 1 X •

>0

К-1 ■ +

і2 і '"ж

М і + <0

а) ф!=±соі, ф2=гЬСйІ (роторы возбуди­телей вращаются в одинаковых на­правлениях)

б) ф!=±С0(, Ф2=±(юі-Ья) (роторы возбуди­телей вращаются в одинаковых на­правлениях)

Гармонические колебания массы М., в направлении 0С6ІХ X 11 у И 1»1аССЫ Мх в направле­нии оси X

Отсутствие ко­лебаний

1 т2е2ш2 IV (со) = Tj - jj X 1

, К ~ 1 М 1 + Мг Я2 - 1

X

м м

в) ф 1=±<вг, (p2==-Fcot (роторы возбуди­телей вращаются в противополож­ных направлени­ях

Гармонические колебания обеих масс только в на­правлении оси х

—. 1 т2е2со2

vV (“)==2 М Х

М

ли

а

%

%

11

Два одинаковых дебалансных вибровозбудителя, установленные на мягко амортизированном твер­дом теле с шестью степенями сво­боды; оси роторов возбудителей совпадают с одной из главных центральных осей инерции тела; плоскости вращения центров тя­жести роторов равноудалены от центра тяжести тела.

См. [42, 57]

12

Та же система, что и в п. 11, но оси возбудителей параллельны плоскости xOz, равноудалены от нее и наклонены под углом я/2—Р к плоскости хGу — плос­

кость вращения центров тяжести роторов; оси Oxyz — главные цент­ральные оси инерции тела).

См. [57, 164, 166]

Вид А

Примечание. Система представляет собой пространственный вариант сйс

Та же система, что и в п. 11, по возбудители не дебалансные, а моногармонические возбуди­тели направленного действия; ли-

Таблица 2 (продолжение) Характер синхронного движения (в пер­вом приближении) Условия устойчивос­ти синхронного дви­жения Выражения для мо~ дулей вибрационных МЭМ0НТОВ W(to) возбудителей несущих тел г) (Pj—±wt, Ф2=+(шг-]-л) (роторы возбуди­телей вращаются в противополож­ных направлени­ях) Масса Мх не­подвижна, масса М2 колеблется только в направ­лении оси у 1 М 1 ~М% X*_i <0 фг=ф2=±шг Круговые по­ступательные ко­лебания парал­лельно плоскости xOz с амплитудой г0=2те,/М М г2 —р~> 2 Щ(С)=- X [ т2е2С02 г м х Mr2 2 1" Ф^ісоі <р2=+(соі-]-л) (роторы возбуди­телей вращаются в противополож­ных направлени­ях) ми п. 7. Прямолинейные поступательные гармонические колебания с амп­литудой А0—2шеіМ, параллельные ли­нии 00 * Режим устой­чив при любых сочетаниях пара­метров (еслп Гф0) W( со) = 1 m2e2co2 Mr2 ~ 2 М Г I I гг X Z 1-І - XZ Ixz= 7Z sin2 Р + +/жС082Р а) Іфі1= ^ІФ2І = І°г Прямолішейньїс поступйтол ьньте гармонически е колебания с амп­литудой An=2m&fllT Л/г* /' >* IV |7,Л — - • • V — / х 1 /г?2Є2(02 2 м х Mr2 і-7-

нии действия вынуждающих сил возбудителей OjOj и о2°2 парал­лельны плоскости xOz, равноуда­лены от нее и наклонены под уг­лом Р к плоскости хОу.

См. [42, 57]

Примечание. Система представляет собой пространственный вариант сис

14

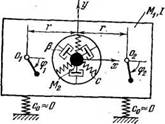
Два одинаковых моногармони - ческпх вибровозбудителя надрав - ленного действия, установленных на твердом теле, которое связано с неподвижным основанием сим­метричной системой упругих эле­ментов и может совершать плос­кие колебания; линии действия вынуждающих сил возбудителей совпадают и удалены от центра тяжести тела на расстояние h.

См. [42, 51, 57]

.2	сх		сф
Рх ~	М ’	ф	м ’
Язе ~	Рх		рф
М '	1 лф -	со

15

Два одинаковых дебалансных вибровозбудителя, установленные на мягко амортизированном твер­дом теле с шестью степенями сво­боды; оси Oxyz — главные цент­ральные; оси возбудителей накло­нены под углом у к плоскости хОу.

См. [57, 118, 163, 164, 330]

Табл. 2 (продолжения Характер синхронного движения (в пер­вом приближении) Условия устойчивое - ги синхронного дви­жения Выражения для мо­дулей вибрационных моментов возбудителей несущих тел параллельные линиям действия возмущающих сил возбудителей OjOj И OgOg Т' _ IxIV. Ixy IxV=Ixcos3P + +1у sin2 p б) ІФхІ— = |<p2+It|=CDt (темы п. 8. Поворотные гармонические колебания Ц отно­сительно некото­рой оси, лежащей в плоскости xOz Mr* г <l а) ІФі1= = |ф2+Л| = (ОІ Отсутствие ко­лебаний і Mh - *2_1 + I X x 4-1<0 ш, 1 m2e2fi)2 (m) 2 м X xU-< + М№ 1 | + ' Ч-‘ 1 б) ІФ11=ІФ»И =Сі)t Плоские непо­ступательные ко­лебания 1 , Mh? X%-i 4 / x x X2 — 1 >0 4> Винтовые гар­монические коле­бания относи­тельно оси z; амп­литуда вертикаль­ной составляющей А0—2т& cos у/М, угловая ампли­туда фо=2 mm sin y! lz Ma2 Me2 / <2+ J + Z X M:(c2+a2 cos2 y) 1 ІУ sin2 v _ 1 т2е2<в2 W (v)— 2 М Х Ма? X sin2 v - j— — z Me2 ^ X M (cs-f-a2cos2 v) I І у sin2 v 1

9 И. И. Блехман

] — передаточное отношение между валами каждого возбудителя

16 Два одинаковых бигармониче - ских дебалансных вибровозбуди­теля, симметрично расположен­ных на мягко амортизированном твердом теле, которое может со­вершать плоские колебания. Плоскости 1—Г и 2—2' осей каж­дого возбудителя параллельны и равноудалены от центра тяжести тела О.

См. [42, 57]

а.		1
	M	e	T%-m
			Am
	jT%
	у

<p,=]t?,+6

х

17

Три дебалансных вибровозбуди­теля, симметрично расположен­ных на мягко амортизированном твердом теле, которое может со­вершать плоские колебания; плоскость осей вращения всех ро­торов проходит через центр тя­жести тела; крайние возбудители одинаковы.

См. [42, 57]

°J e. t.	0,0з °z
5^ *Т*‘Н m ™ m,

с„~0

18 Четыре одинаковых дебаланс­ных иибровозбудителя, симмет­рично расположенные на мягко амортизированном твердом теле, которое может совершать плоские колебания.

См. [42, 57]

Примечание. Об устойчивости режимов, в которых отсутствуют Кодебания

Табл. 2 (продолжение) Характер синхронного движения (в пер­вой приближении) Условия устойчивос­ти синхронного дви­ Выражения для мо­дулей вибрационных моментов возбудителей несущих тел жения W(m) q>i=±G>t ф2=±(0І Прямолинейные поступательные бигармонические колебания парал­лельно оса Ох по закону 2 те х — м cos cot - f- 2т'е' + ~~м - coajfeof Режим устой­чив прн любых сочетаниях пара­метров, однако мо­гут быть устойчи­выми также и иные синхронные режимы. При /=2 такие побочные режи­мы отсутствуют, если 4то'е'Сте фі=ф*=±в>*» Фз==Ь(соЯ-я) (роторы всех воз­будителей враща - ются в одинако­вых направлени­ях) Круговые по­ступательные ко­лебания с ампли­тудой 2me — mgej г°“ М Mr* ^ тзЪз I те а) Фі=±сог, ф2=±(«>Н-я), ф3==р(соі-]-п), ф4==рші (роторы 3-го и 4-го возбудителей вра­щаются в направ­лении, противопо­ложной направле­нию вращения ро­торов 1-го и 2-го возбудителей) б) ф1=±ЮІ, ф2=±(соі+л), фг=±£0«, Ф4=±(о>г+я) (роторы всех воз­будителей враща­ются в одинаковых направлениях) Отсутствие ко­лебаний Режимы’ устой­чивы прн любых сочетаниях пара­метров

•«сущего тела, для систем более оощего вида см. п. 4 § 8 и пп. 6 и 7 § 14 гл. 3.

19

Два одинаковых дебалансных вибровозбудителя или вибровоз­будителя направленного действия, установленные на шарнирно опер­той балке однородного сечения с равномерно распределенной мас - .сой.

См. [57, 330]

. Ы. Р Щ___________ №

Ж?.

ж

ESf— изгибная жесткость, р — погонная плотность балки

Примечание. О случае мягко амортизированной балки с произвольным чис

20

Один дебалансный (1) и один «пассивный» (лишенный двигате­ля) внешний планетарный вибро­возбудитель (2), коаксиально ус­тановленные на свободном твер­дом теле (3), которое может совер­шать плоские колебания.

См. [251, 252, 42, 57]

Примечание. Результат остается справедливым и в случае, когда планетар

Табл. 2 (продолжение Характер синхронного движения (в пер­вом приближении) Условия устойчивос­ти синхронного дви­ Выражения для мо­дулей вибрационных моментов возбудителей несущих тел жения W(co; Упругие коле­бания под дейст­вием синфазных гармонических возмущающих сил Р—тг<х>2, приложенных в точках ох и о2 W (to) т2є2<о4 - 2 Х X 1 Л (со*)f б) |ф1| = (й(, |ф4|=СйІ+Я Упругие коле­бания под дейст­вием противофаз­ных возмущаю­щих сил F—me w2, приложенных в точках ох и о2 А:(со2)<0 лом одинаковых возбудителей направленного действия см. работу [212], а также [57]. Фі = ± (wt + я + + Р' + arcsin q), ЄЬ. , g = ып p', ,s4t jp2=±t0(, si0=mdejma, p'=arctg /' (/'— коэффициент сопротивления перекатыванию), та=М—ть Круговые по­ступательные ко­лебания Режим устой­чив во всей обла­сти своего сущест­вования, опреде­ляемой неравен­ством еь У І + (Я2 & < Г ’ если k. Jkj^i (ks — суммарные коэффициенты демпфирования)

1тый возбудитель является внутренним.

21

Два одинаковых дебалансных вибровозбудителя и один пассив­ный внутренний планетарный вибровозбудитель, симметрично установленные на мягко аморти­зированном твердом теле, которое может совершать плоские колеба­ния.

См. 142,57]

VI + (Ла Г

2. Ревультат

ь

Примечания: 1. Режим существует при - яг-

Si о

изменении числа этих степеней свободы результат, как правило, существенно изменяется (см. п. 2 § 11 и п. 8 '§ 14).

6) Системы, представленные в пп. 2—5, 7, 8, 14, 16—18, 20 л 21, являются частными случаями системы, рассмотренной в п. 5 § 8 (рис. 12), а системы, представленные в пп. 11—13 и 15 — частными случаями системы, изученной в работе [163].

7) Для возможности практического применения большинства приводимых схем необходимо наряду с условиями устойчивости также выполнение условий стабильности фазировки (см. § 9).