От плотности упаковки смеси зерен песка и щебня (гравия) зависят многие технологические свойства бето­на. При исследовании этого вопроса и выявлении мате­матических зависимостей пользуются моделью фиктив­ного грунта, состоящего из шаров одинакового диаметра. Плотность упаковки соприкасающихся шаров в такой модели зависит от их взаимного расположения и может быть определена по формуле

Dm ------------------- Я. (6.4)

6(1 — Cos 6) V 1+2 Cose

Согласно (6.4), плотность расположения шаров одного диаметра характеризуется углом 0, образованным гра­нями ромбоэдра. В зависимости от взаимного располо­жения шаров угол 0 может изменяться от 60 до 90° и в соответствии с этим Dm будет иметь значения от 0,741 до 0,524. По Dm можно вычислить пустотность такой моде­ли, а именно:

Шп— — Dm. (6.5)

При указанных крайних значениях 6 пустотность тп может меняться в следующих пределах:

0,2595 <тп< 0,4764.

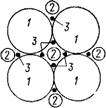
Плотность упаковки рассмотрен­ной модели можно значительно уве­личить, если в пустоты между кру­пными (основными) шарами без их раздвижки поместить шары мень­шего диаметра (рис. 6.1). Шары 2, точно помещающиеся в каждой пу­стоте, образованной основными ша­рами назовем «помещающими­ся», а шары с гораздо меньшими диаметрами, располо­женные между шарами — «заполняющими» (2 и 3).

При упаковке шаров по схеме рис. 6.1 соотношение их диаметров выражается зависимостью

V-i)==0'l56dn' (6'6>

Где Dn—диаметр основных шаров; T)—диаметры меньших по величине заполняющих шаров.

Если учесть, что между шарами возникает трение, препятствующее их компактной упаковке, то соотноше­ние (6.6) должно быть несколько уменьшено и будет равно [5]:

^> = 1/7^. (6.7)

Из (6.7) следует, что для полной упаковки каждый сле­дующий диаметр шара. должен быть в 7 раз меньше пре­дыдущего, т. е. плотность упаковки шаров различного диаметра возрастает по прогрессии 1/7, 1/72, 1/73 и т. д.

Допустим, что единица объема шаров диаметром d{==20 мм характеризуется величиной D1 = 0,524 и 1щ — = 0,476. Добавляя 0,476 объемных единиц шаров диа­метром d2—1/7-20 = 2,8 мм, получаем т2 = 0,476-0,476 = = 0,226 и D2 = 0,774. Внесем в эту систему шаров 0,22 объемных единиц шаров диаметром d3=l/7-2,8 = = 0,39 мм, тогда т3=0,476-0,22 = 0,105 и D3=0,895, и, наконец, при наполнении системы шаровыми части­цами 1/7-0,39=0,054 мм в количестве 0,105 объ­емных единиц будем иметь т4=0,476-0,105=0,05 и £>4=0,95.

В соответствии с приведенными расчетами объемное содержание каждой фракции шаров, м3, может быть определено по зависимости

Vn = Dm~Dw (б-8)

В таком случае плотность упаковки шаров Dm=0,95 по принятой прогрессии достигается при следующем объем­ном содержании каждой из четырех фракций шаров: D1 = 20 мм —0,524 м3, или 55,4%; D2 = 2,8 мм — 0,250 м3, » 26,2%; ^з = 0,39 мм —0,121 м3, » 12,7%; = 0,054 мм —0,055 м3, » 5,7%.

Подобный расчет плотности упаковки может быть приве­ден и для шаров с любым другим соотношением их диа­метров