На основании рассмотренных закономерностей изме­нения плотности упаковки и пустотности песка и щебня (гравия) можно сделать следующие выводы. Если в сме­си песка и щебня (гравия) между двумя смежными фракциями зерен соблюдается определенное отношение ак (допустим, равное 2), то в таком случае упаковка зе­рен данной формы будет тем плотнее, а пустотность тем меньше, чем больше различных фракций зерен содер­жится в смеси.

Для подтверждения выдвинутого положения восполь­зуемся теоретическими представлениями о плотности упаковки зерен упорядоченного гранулометрического состава, в основу которых положена схема, приведен­ная на рис. 6.3, а [154].

Допустим, что смесь состоит из трех фракций зерен одинаковой формы, но разной крупности: d(n-i), ап, d^n+1> и расстояния между ними равны соответственно: S(N-I), Sn, S(n+i). При объеме одного зерна Vm=$Kdh (для ша­ра pK=jt/6) плотность упаковки п — числа зерен диа­метром dm>dn в воображаемом геометрическом объеме (вместимости) сосуда определяется выражением

Заполним емкость VE таким же количеством п зерен диаметром dn естественно, что суммарный объем всех зерен будет меньше, чем в первом случае, а следователь­но, и меньше показатель плотности их упаковки:

Разделив Dm на Dn, получим

Dm/dn = (Dm/D„)1/3.

Из рис. 6.3,6 следует, что Sn=dm—Dn. На этом основа­нии можно написать

Dm Л1/3

, 1-

Dn Dn

Подставляя полученные выражения в Sn, будем иметь

Sn =

— 1

Dm VI3

Dn. (6.9)

Dn

Формула (6.9) позволяет определить расстояние Sn меж­ду смежными зернами различной крупности в зависимо­сти от плотности их упаковки в данной емкости.

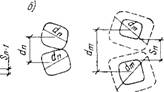
Рис. 6.3. Схема компоновки зерен заполнителя при оптимальной плотности упаковки

^ ^ ("А Д Даоот

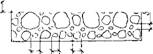
Sn-1 dn-z dn-f

18—634 273

Для того чтобы зерна следующей (более мелкой) фракции d{n-1) могли поместиться в пустотах между зер­нами dn, должно выполняться условие Sn^d(n-i), в свя­зи с чем при прогрессии ак=2 должно быть При несоблюдении этого условия гранулометрия фрак­ций будет нарушенной и плотность упаковки смеси зе­рен различной крупности уменьшится. Рассмотрим это на примере.

Предположим, что в емкость VE, которую примем за единицу, помещена смесь зерен крупностью от d по dn И допустим, что количество фракций п<1т. Обозначим через /Сап отношение объема, занимаемого зернами круп­ностью dn к VE, т. е. плотность упаковки каждой фрак­ции зерен, содержащейся в смеси заполнителя. В таком случае пустотность смеси зерен тсм, состоящей только из фракций крупностью от d(n+до dm, будет равна

Т

™см = 1 ~ 2 П+1

Т

Где 2 — плотность упаковки смеси зерен заполнителя после по-

Л+1

Следовательного исключения из нее отдельных фракций.

В таком случае расчетный показатель плотности упаковки зерен отдельных фракций в смеси заполнителя может быть представлен в следующем виде;

Dan = кап/тсм = Кап/ ^ 1 - S ) . (6.10)

Если известны гранулометрические составы песка и щебня (гравия) и экспериментально определен показа­тель плотности их упаковки в смеси, тогда, пользуясь полученными зависимостями, нетрудно определить, ка­ким образом следует изменить гранулометрический сос­тав, чтобы добиться максимальной плотности упаковки зерен.

Пример. Допустим, что смесь песка и щебня состоит из восьми фракций зерен одинаковой формы и соблюда­ется прогрессия ак=2. Требуется определить, при каких условиях можно получить практически максимальную плотность упаковки Dc, равную 0,85, если в виброуплот­ненном состоянии уп= 1,886 т/м3 и ущ= 1,720 т/м3.

Для решения этой задачи воспользуемся данными табл. 6.3, в которой помещены гранулометрические со-

ТАБЛИЦА 6.3. СОПОСТАВЛЕНИЕ ГРАНУЛОМЕТРИЧЕСКОГО СОСТАВА СМЕСИ ЩЕБНЯ И ПЕСКА Грануломет- Приведенный диаметр зерен, Мм, при ак=2 Рический состав и рас­ | D2 Dz 1 D5 | * 1 Ds Четные па­раметры 0,11 0,23 0,45 0,90 1,60 3,33 6,67 13,35 Щебень, % Песок, % 2,10 15,95 21,00 33,10 11,60 8,50 16,25 36,50 55 V% 0,69 5,23 6,88 10,85 3,80 11,04 24,54 36,97 *a„=Dc Рп 0,005 0,041 0,054 0,085 0,030 0,086 0,191 0,288 Т 2 К =D ~ n+1 а с 0,775 0,734 0,680 0,585 0,56 > 0,479 0,288 0 . П ~2 К 1 а Т См 0,225 0,266 0,320 0,405 0,435 0,521 0,712 1 D = А п 0,022 0,154 0,169 0,210 0,070 0,165 0,268 0,288 = К /т А п см D Т 0,711 0,711 0,711 0,711 0,711 0,711 0,711 0,711 S П 0,240 0,154 0,277 0,450 1,868 2,090 2,555 4,680

Ставы песка и щебня и приведены рассчитанные по фор­мулам параметры.

Из табл. 6.3 следует, что плотность упаковки каждой фракции щебня и песка в отдельности — Dm = 0,711 или rnm=0,289, т. е. одинакова, и это совпадает с экспери­ментальными определениями (см. табл. 6.1). Далее вид­но, что фракция песка не уменьшается в просветах (пустотах) между фракциями D7, так как S7<d6. Это же относится к фракции щебня D7Y поскольку D7<Cds. Для оптимизации гранулометрического состава смеси щебня и песка необходимо изменить их процентное содержание в смеси так, чтобы соблюдалось условие Sn^d(U-), при котором достигается максимальное значение Dc.

Т

При показателе плотности Dc= 1 и тСш=^Кх фор-

Л+1

Мулу (6.10) можно представить в виде:

Dan=/V)-/>,(„-,) . u=Kt (6Л1)

18*

275

РЦП) Pt(n)

Где pt(n) й pt(n-i) — число зерен каждой фракции, проШедШих через отверстия сит; Pn = Pt(n)—pt(n-О соответствуют остаткам на ситах.

По формуле (6.11) видно, что отношение наиболее крупных фракций ко всему количеству, прошедших че­рез сита pt(n), — величина постоянная. Согласно зависи­мости (6.11), количество наибольшей фракции, которое проходит через сито, может быть определено уравне­нием:

Рп = Рцп) —Pt(N-1) = Рцп)

При рЧп)= 1, Рп= 1 - Ю = К°-К1.

Для всех остальных фракций аналогично будем иметь

(6.12)

Р(п-~ 1) = Pt(N-L) ~ Pt(N-2) = Pt(N-L) ~~ КрЦп-1) =

= (1 - К) рНп_г) = (1 - К) Крт = {К} - К*) Рцп)- Р(/1_2) = К* - К3; Р(п-з) = К3-К4 и т. д. Для прогрессии ак = 2 получим

Отсюда следует, что

^, = 0^3,375 = 0,2960,

Пользуясь формулой (6.12), можно подбирать компо­зиции заполнителей для бетона с заданным показателем плотности упаковки смеси зерен различной крупности Dc при известных плотностях упаковки каждой фракции, т. е. удельных фракционных плотностях Dm.

При Ап=0,71 (см. табл. 6.3); Z)n=0,296.0,71 =0,21 и /С1 — 1—Dn = 0,79 можно определить содержание от­дельных фракций в смеси зерен щебня и песка, обеспе­чивающих получение Dc=0,85 (табл. 6.4).

Согласно табл. 6.4, показатель плотности упаковки Dc=0,848 и минимальная пустотность min тСм=0,152 может быть достигнута путем смешивания щебня с Тщ= 1—1,72/2,61 = 0,34 в количестве 44,4% и песка тц= 1 — 1,886/2,63=0,283 в количестве 55,6%. Это сви­детельствует о необходимости соответствующего измене­ния гранулометрических составов щебня и песка.

Приняв за основу рассчитанный гранулометрический состав смеси щебня и песка (см. табл. 6.4), можно пока­зать, как будут изменяться значения Dc и min mc, если

ТАБЛИЦА 6.4. РЕЗУЛЬТАТЫ РАСЧЕТА ОПТИМАЛЬНОГО ГРАНУЛОМЕТРИЧЕСКОГО СОСТАВА СМЕСИ ЩЕБНЯ И ПЕСКА

Содержание от­дельных фрак­ций, %

Параметр Рп^КО-К1 Ро»-^*8-*4

Расчетные значения па­раметра р

(П—т)

1—0,79=0,21 0,79—0,624=0,166 0,624—0,493=0,131 0,493—0,389=0,104 0,389—0,308=0,081 0,308—0,243=0,065 0,243—0,198=0,051 0,192—0,152=0,040

Исключить или добавить отдельные фракции щебня и песка (табл. 6.5).

Из табл. 6.5 следует, что показатель плотности упа­ковки зерен Dc = 0,848 может быть получен как при со­держании двух фракций щебня в количестве 44,4% и песка — 55,6%, так и при содержании в смеси трехфрак- ционного щебня в количестве 59,8% и пятифракционного песка — 40,2%. При изъятии из песка двух фракций смесь, содержащая 50,35% песка и 49,67% двухфракци- онного щебня, характеризуется значениями Dc = 0,757 и min mCM=0,243.

Расчетный метод подбора оптимального грануломет­рического состава смеси щебня и песка, при котором в каждом конкретном случае достигается плотная их упа­ковка, позволяет получить результаты, которые имеют хорошую сходимость с экспериментальными данными.

Подобрав указанным методом гранулометрический состав щебня и песка, когда пустоты каждой восходящей по крупности фракции заполняются без их раздвижки фракциями меньшего размера, при данном показателе ак можно путем графического построения определять изменение тсш в зависимости от содержания в смеси щебня и песка. Для этого по оси ординат откладывают значения тСШу а по оси абсцисс, один под другим, соот-

ТАБЛИЦА 6.5. ВЛИЯНИЕ ГРАНУЛОМЕТРИЧЕСКОГО СОСТАВА СМЕСИ ЩЕБНЯ И ПЕСКА HA DQ И min т{ Приведенный диаметр зерен, мм, при ак=2 Си® Я М Параметр Dt D2 Dz 1 D5 Dti 1 D7 D, Do Зн о 0,11 0,23 0,45 0,90 1,60 3,33 | 6,67 13,35 26.7 1 Рп 0,040 0,051 0,065 0,081 0,104 0,131 0,166 0,210 Тщ(п)> % 4,7 6 7,7 9,5 12,3 15,4 19,6 24,8 — Dc, min /72см 0,848; 0,152 Рп 0,40 0,051 0,065 0,081 0,104 0,131 0,166 0,210 2 Тщ(п)> % 4,7 6,0 7,7 9,5 12,3 15,4 19,6 24,8 £>с, Min mCM 0,848; 0.152

	0,065	0,081	0,104	0,131	0,166	0,210
	8,58	10,70	13,75	17,30	21,93	27,74

0,757; 0,243

Dc, min Тсм

Ветственно процентное содержание песка от 0 до 100 и щебня (гравия) от 100% до 0, разделив обе оси абсцисс на десять равных частей.

Отложив на оси ординат экспериментально опреде­ленные значения тщ(тгр) при пщ(птр), равном 100% и пп=0, а гпи при тщ(гпгх>)=0 и пп=100% и затем minmCM при соответствующем процентном содержании щебня и песка, получим три точки, которые соединяют двумя прямолинейными отрезками. Ломаная кривая, проведенная указанным способом, будет характеризо­вать изменение пустотности смеси щебня и песка опти­мального гранулометрического состава в зависимости от их процентного содержания в смеси. При более точном изображении этой зависимости через три точки следует провести кривую, координаты которой могут быть опре­делены при помощи приведенного расчетного метода. Однако, учитывая громоздкость вычислений и пологость кривой, ее с достаточной степенью приближения можно заменить двумя прямолинейными отрезками.

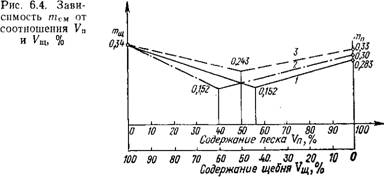
В качестве примера на рис. 6.4 показано графическое изображение зависимости тсм от процентного содержа­ния в смеси щебня и песка, выполненное по данным табл. 6.5. Из графика видно, что minwCM зависит в каж­дом конкретном случае в основном от гранулометричес­кого состава песка. При одинаковом зерновом составе щебня (кривые 1 и 3) и различном песке 1 м3 сухой сме­си получаем при увеличенном содержании щебня и большем значении min тсм (кривая 3). С другой сторо­ны, при практически одинаковом гранулометрическом составе песка (кривые 1 и 2) minmCM=0,152 достигает­ся как при двух-, так и при трехфракционном щебне, однако в последнем случае (кривая 2) в смеси с песком его требуется больше. Для данного гранулометрического состава смеси щебня и песка по графику на рис. 6.4 можно определить тсш при различных их количествен­ных соотношениях.

График изменения пустотности смеси щебня и песка Шсм в зависимости от соотношения их объемов, анало­гичный рис. 6.4, может быть построен другим способом [4]. Результаты вычисления показывают, что тсм, опре­деленные по объемным массам щебня и песка в рыхло - насыпном, а не виброуплотненном состоянии практичес­ки совпадают со значениями тСШу приведенными на рис. 6.4. В этом случае создаются более благоприятные условия, при которых меньшие по размеру фракции мо­гут расположиться относительно более крупных без их раздвижки. Отсюда следует, что оба графоаналитичес­ких способа построения зависимости MCM=F(VTU Ущ)> по существу, равноценны.