Плотность пены зависит от соотношения жидкой н газовой фаз и может колебаться в пределах от 0,5 рж (р« — плотность жидкой фазы) до значений, близких к нулю. Так, плотность пен, применяемых при тушении пожаров или для вытеснения дыма из помещений, составляет 1—0,5 кг/м3 и меньше.

Плотность пены можно математически связать с другим свойством — удельной поверхностью 5 раздела фаз раствор — газ. Объем газа Vr в единице объема пены с плотностью р со­ставляет

TOC o "1-3" h z Vr = 1-Р/Ак (2.4)

Из уравнения (2.4) получим:

DVr = —йр/рж (2.5)

Выражение (2.5) подставим о уравнение состояния пены (газов), в котором величина р должна учитывать среднее гид - - ростатическое давление столба пены:

P = P + pgh/2 (2.6)

где р — среднее давление внутри пузырька, р — давление в пузырьке без уче­та гидростатического давления столба пены; g — ускорение свободного паде­ния; h — высота столба пены.

Гидростатическое давление по сравнению с атмосферным мало, и им можно пренебречь. Тогда имеем:

Зрф/рж — 2 AdS = 0 (2.7)

Из уравнения (2.7) получим:

(Ро — Р) = (S0 — S) (2.8)

3 р

Где ро и S0 — соответственно начальные значения плотности пены и площади поверхности раздела.

Выражение (2.8) показывает, что в процессе разрушения пе­ны уменьшение поверхности раздела сопровождается одновре­менным уменьшением плотности.

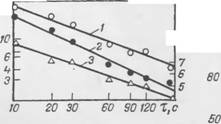
Рис. 15. Изменение среднего диаметра пузырьков и истинной удельной по­верхности пены во времени.

Кратность пены — 25.

Дисперсность пен можно оценить средним диаметром пу­зырьков, удельной поверхностью раздела раствор — воздух или распределением пузырьков по размерам. Обычно размеры пу­зырьков образующейся пены имеют широкий диапазон — от со­тых долей миллиметра до нескольких сантиметров. Лишь i особых случаях можно получить монодисперсную пену, исполь­зуя специальные устройства. Поэтому применять средний диа­метр пузырьков для оценки дисперсности пен, особенно с ячей­ками многогранной формы, не вполне правомерно, хотя и до­пустимо.

На дисперсность пен существенное влияние оказывают фи­зико-химические свойства раствора (поверхностное натяжение, вязкость, концентрация ПАВ и т. д.), способ смешения фаз, кон­струкция генератора "пены или технологического аппарата, а также режимы ведения технологического процесса, в ходе ко­торого образуется пена.

Диаметр пузырьков пены в незначительной степени увели­чивается с уменьшением концентрации ПАВ. Это связано, глав­ным образом, с изменением поверхностного натяжения рас­твора.

Й, мнм

&Ю? м*/Г

160 Г, с

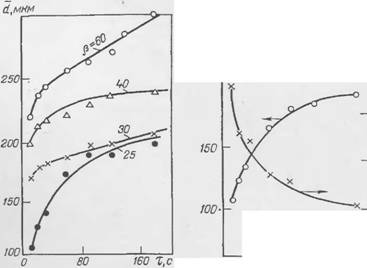
Рис. 14. Изменение среднего диаметра пузырьков пей различной кратности Во времени.

М

Более существенно влияние конструкции аппарата и режима ведения технологического процесса, сопровождающегося пено - образованием. Степень развитости поверхности контакта жид­
кой и газовой фаз особенно важна в аппаратах, предназначен­ных для проведения различных химических процессов в пенном слое. Одна из особенностей этих аппаратов состоит в том, что в слое турбулентной иены происходит многократное обновление поверхности контакта фаз, продолжительность су1дествования пузырька пены исчисляется сотыми долями секунды. Поэтому при расчете истинной поверхности раздела фаз (или среднего диаметра пузырька) необходимо учитывать динамическое со­стояние пены с помощью коэффициента, характеризующего кратность обновления поверхности. Уравнения, описывающие зависимость поверхности контакта фаз от различных факторов, как правило, выводят эмпирически, и они справедливы лишь для аппаратов данного типа.

При постоянной интенсивности перемешивания фаз, когда кратность нены изменялась вследствие незначительных пзмене-

Время с момента образования пеиы (в с): 1 — 15; 2 — 30; 3 — 60; 4 — 120.

5 —С--------- 1-------- 1-------- 1----

31+0 d, MKt.

Рис. 18. Интегральное распределение числа пузырьков пены по размерам (в нормально-вероятностной системе координат).

Время с момента образования пены (в с): 1 — 15; 2 — 30; 3 — СО; 4—120.

Ннй расхода воздуха, были получены данные, характеризующие увеличение среднего диаметра пузырьков при возрастании кратности пены [51].

Между размерами пузырьков и стабильностью пены имеется определенная связь: для данного пенообразователя и условий получения пены существует некоторый интервал размеров пу­зырьков, обладающих наибольшей стабильностью.

AS/S,°/o

S-10'^M%3 ЯАп/П, %

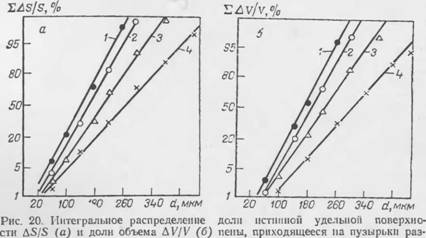
Рис. 17. Изменение доли истинной удельной поверхности пены, приходя­щейся на фракции пузырьков 120— 160 мкм (1) и 80—120 мкм (2), V Всей истинной удельной поверхно­сти (3) во времени.

-10 85-

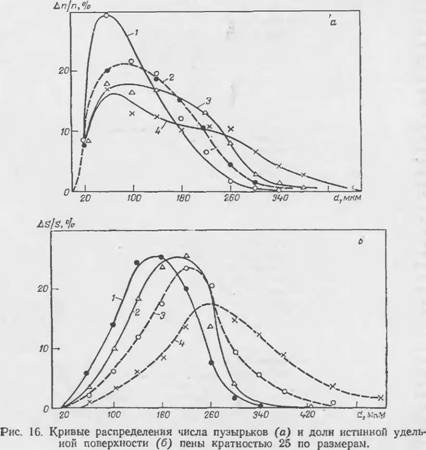
На примере неиы, приготовленной из 1%-ного водного рас­твора смеси сульфонола НП-1 и тринатрийфосфата в отношении 1 : 1 (масс.) путем барботирования воздуха через раствор, изу­чали изменение дисперсного состава пен во времени. На рис. 14 приведены данные об изменении среднего диаметра пузырьков пен различной кратности [67]. Рис. 15 показывает, что наибо­лее интенсивные изменения в дисперсном составе пены протека­ют в начальный момент после ее _образования и только через 80—100 с изменением параметров d И S становится близким к линейному. Зависимость изменения удельной поверхности пены во времени можно выразить некоторым уравнением вида у=ахь, вполне удовлетворительно описывающим изменение дисперсного состава пены во времени [53]. На основании экспе­риментальных данных были построены кривые распределения пузырьков по размерам в зависимости от времени, прошедшего с момента приготовления пены, а также кривые, характеризую­щие долю поверхности раздела, приходящуюся на фракции пу­зырьков различных диаметров (рис. 16). Приведенные кривые показывают, что полидисперсность пены с течением времени значительно увеличивается. В начальный момент после обра­
зования пены наиболее вероятны пузырьки, имеющие средний диаметр от 60 до 100 мкм, а наибольшая поверхность раздела фаз принадлежит пузырькам от 100 до 180 мкм. Доля поверх­ности раздела, приходящаяся на пузырьки фракции 80—120 и 120 ИИ) мкм, резко сокращается ц<> нроменн [Г>1]. а заткчшо - стн AS/S—т п i'—т удовлетворительно описываются уравнением прямой в полулогарифмических координатах (рис. 17).

При иаиесешш данных (см. рис. 16) на график с пор мал мю - всроятноспюн ceiKoii получены зависимости, приведенные па рис. 18. Прямолинейный характер интегральных кривых распре­деления показывает, что они близки к нормальному закону (с усечением). Некоторые отклонения для самых мелких и крупных пузырьков объясняются их малым статистическим ве­сом. Это отклонение наблюдалось и для жировых шариков мо­лока [68].

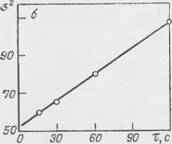
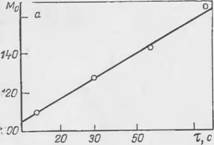
1 По методикам расчета, изложенным в работе [69], были рассчитаны основные параметры нормального распределения пузырьков но размерам (математическое ожидание М, диспер­сия а2). Эти параметры изменяются в процессе старения иены (рис. 19), характер их изменения может быть выражен эмпири­ческими соотношениями

Mo = 601gx-f 40 с2 = 0,45т+ 53 (2.9)

Поскольку дифференциальные кривые распределения несиммет­ричны (см. рис. 16), для них вычислены значения асимметрии А(х) и эксцесса Е(х) путем определения начальных и централь - пых моментов [69]:

Время с момента обра - 15 30 60 120 моплпия йены, с

Значение аснмметрнн 0,58 0,34 0,38 0,525 А(х)

Значение эксцесса Е(х) —0,22 —0,62 —0,44 —0,70

Описанный характер распределения пузырьков по размерам наблюдали и для пен, полученных в других условиях [40].

Рис. 19. Изменение математического ожидания (а) и среднего квадратическо - - о отклонения (б) для распределения пузырьков пены по размерам во вре­мени.

-952 33

Личных фракций (в нормально-вероятное гной системе координат). Время с момента образования пены (в с): / — 15; 2 — 30; 3 — 60; 4 — 120.

Были рассчитаны значения доли не шпион удельной поверх­ности AS/S и доли объема AV/V, приходящиеся па пузырьки различных фракции. Результаты расчетов, представленные на рис. 20, показывают, что и в данных случаях полученные кри­вые распределения вполне удовлетворительно описываются нормальным законом.

Для описания распределения пузырьков в пене по размерам был использован закон Пуассона [70] па основе следующего формализованного подхода. Общее число пузырьков в пене очень велико. Вследствие полиднсперсностп иены диаметр пу­зырьков принимает значения от единиц до сотен микрометров. Поэтому вероятность нахождения в системе пузырька с опреде­ленным диаметром стремится к нулю, что соответствует основ­ному содержанию закона редких событии.

Обозначим п — порядковый номер классов размеров пузырь­ков; N — число событий (число пузырьков данного класса). Так как классы одинаковы по размеру, п= 1 для класса 0-^40 мчм; П = 2 для класса 40-f-80 мкм и т. д. В соответствии с работой [71] N и п связаны зависимостью

Lg(A/-n!) = Јm + 6 (2.10)

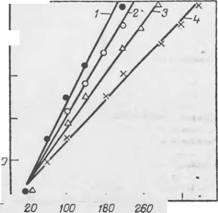
Приведенные на рис. 21 данные свидетельствуют о том, что распределение пузырьков (для т от 15 с до 2 мин) весьма близ­ко к теоретическому распределению Пуассона. Чем дольше про­должительность существования пены от момента ее образова­ния, тем больше угол наклона прямой к оси абсцисс н меньше размер отрезка на оси ординат. При этом параметры а и b Уравнения (2.10) линейно изменяются с увеличением времени (рис. 22).

Процесс изменения дисперсного состава ней протекает таким образом, что при разрушении пены сохраняется некоторая об­ласть критического размера пузырьков, доля которых остается постоянной по времени (п=4—5; d= 120—200 мкм).

(2.11)

Анализ данных рис. 21 и 22 позволил получить уравнение, описывающее распределение пузырьков по размерам в зависи­мости от времени т их существования (в мин):

It' (N-iU) - (0,! г 0,5) и — 0,5с 2,2

Применимость закона Пуассона для описания распределения пузырьков по размерам ограничена для пузырьков больших размеров, если их общее число невелико, а также для пен, под­вергшихся значительному распаду