ПЕРЕМЕЩЕНИЯ КРОМКИ ПЛАСТИНЫ ПРИ НАГРЕВЕ ЕЕ ДВИЖУЩИМСЯ ИСТОЧНИКОМ ТЕПЛА
 14 марта, 2016
14 марта, 2016  Oleg Maloletnikov
Oleg Maloletnikov Образование поперечной усадки и связанных с нею поперечных напряжений оу является одним из основных вопросов теории сварочных напряжений и деформаций. Особое внимание привлек к себе этот вопрос в связи с появлением способа электрошлаковой сварки, когда временные поперечные деформации стали оказывать непосредственное влияние на зазор при сварке, сварочный режим и деформации конструкции.
В основе механизма образования поперечной усадки лежат перемещения кромки пластины, нагреваемой сварочным источником тепла. Для определения этих перемещений с успехом могут быть использованы методы теории упругости. Известно, что упругое решение задачи в перемещениях является первым приближением точного упруго-пластического решения задачи. После некоторых уточнений первое приближение может быть использовано для решения практических технологических задач.
Для определения перемещений наметим следующий план:
1. Определение напряжений в бесконечной пластине от элементарного линейного мгновенного источника тепла.
2. Разрезка бесконечной пластины на две полубесконечных, снятие напряжений ае по кромке пластины и определение перемещений кромки от мгновенного источника тепла.
3. Суммирование перемещений от отдельных источников тепла за весь период сварки.
Ранее [формула (17)] были найдены напряжения о, от линейного мгновенного источника тепла. Запишем эту зависимость с учетом теплоотдачи в воздух:
|
Р (t) — функция теплоотдачи. 30 |
,-^-/узрс/гилі iwiaumnj на дис nutiia п ирили/лим пи ijjaiu iiaii|J>i"
жения Of Снятие напряжений ot вызовет перемещение прямолинейного края пластины. Для определения перемещения вточкеО воспользуемся формулой U 10]
v^JEp[n^Tdr ~1irpdr' <32>
где Р — °i — распределенная нагрузка (рис. 15);
d — произвольная постоянная величина.
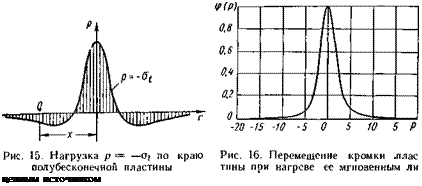 |
В нашем случае распределенная нагрузка р действует слева и справа от точки 0 с координатой г — х, для которой определяется перемещение.
Перенесем начало координат в точку х и проинтегрируем в пределах от 0 до оо нагрузки слева и справа от точки х. После преобразований получим
х2
После разложения sh в ряд и интегрирования находим
X
p = vu-
Выражение (34) описывает кривую перемещения кромки пластины от нагрева мгновенным линейным источником. В дальнейших расчетах присвоим перемещениям кромки знак плюс в отличие от знака минус в формуле (34).
в (К 3 Рис' ^ показаны значения функции ф (р), заключенной фигурные скобки формулы (34). Ординаты кривой на рис. 16
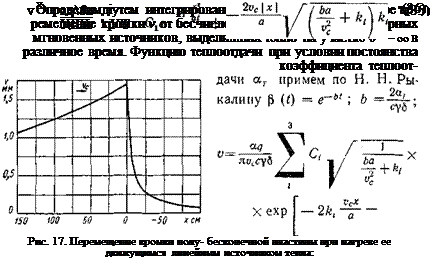 |
пропорциональны перемещениям кромки от нагрева мгновенным источником. Вводя заменяющую функцию <р (р)3 ^ <р (р), находим
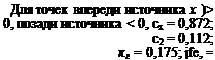 см2/се к; су =
см2/се к; су =
■4 I/СЄК,
с3 = 0,016,
= 0,022; jfe, = 0,003
На рис. 17 показана типичная кривая перемещений кромки полубесконечной пластины, нагреваемой движущимся линейным источником тепла. В случае сварки двух пластин кромки движутся навстречу друг другу, свариваются, а затем после остывания дают поперечную усадку шва. Можно отметить два обстоятельства, вытекающие из полученных результатов.
1. Площадь, заключенная под кривой перемещений для мгновенного источника (см. рис. 16) или для непрерывно-действующего движущегося источника (см. рис. 17), пропорциональна 2а, а не а. Это также следует из закона изменения объема (п. 5) — приращение площади листа от нагрева, пропорциональное коэффициенту 2а, полностью реализуется в перемещении края листа.
2. В случае отсутствия теплоотдачи (Ь = 0) перемещение кромки позади источника остается постоянным сколь угодно долго, даже при остывании и сокращении металла кромки.
Полученные результаты позволяют вскрыть механизм поперечной усадки и вывести количественные соотношения ДЛЯ определения временных и остаточных поперечных деформаций.

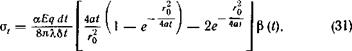
 Опубликовано в
Опубликовано в