В 1954 г. в России М. JI. Новиковым было разработано зубчатое зацепление с круговыми профилями зубьев (рис. 8.49). Обладая рядом положительных качеств и в первую очередь повышенной нагрузочной способностью, передачи Новикова получили широкое распространение. В России они стандартизованы. Передачи изгото­вляют общего и специального назначения.

Особенности зацепления. Непрерывность движения прямозубой эвольвентной передачи обеспечивается только при торцовом коэф­фициенте перекрытия еа>1. Косозубые эвольвентные передачи имеют два коэффициента перекрытия: торцовый еа и осевой Косозубая передача может работать и при еа=0, если еР> 1. При этом не обязательны сопряженные профили зубьев. Проиллюст­рируем это на рис. 8.50, где тонкими линиями изображено зацепле­ние прямозубой передачи с эвольвентными зубьями. В данный момент в зацеплении находятся две пары зубьев 1 и 2. Точки зацепления а и Ъ расположены на линии зацепления АхАг. Эволь­вентные профили являются сопряженными, так как контакт этих зубьев сохраняется на всем протяжении активного участка Ga линии зацепления. Напомним, что Ea=GJPb- Далее допустим, что у колеса 1 эвольвентные профили заменены круговыми (изображены жирно). При этом дуги окружностей касаются эвольвент зубьев этого колеса в точках а и аъ а радиусы Г меньше радиусов кривизны эвольвент. В момент, когда первая пара кругового зуба колеса 1 и эвольвент - ного зуба колеса 2 зацепляется в точке а, зацепления второй пары таких зубьев нет. Вторая пара вступит в зацепле­ние только тогда, когда она займет положение первой пары, т. е. в точке а. При переходе за точку а зацепления снова не будет, между зубья­ми образуется зазор.

Таким образом, зацепление кругового и эво - львентного зубьев прямозубой передачи может существовать только в одной точке. Длина суще­ствовавшей ранее активной линии зацепления Ga сокращается до нуля (еа=0). Такие профили называют несопряженными. Прямозубая переда­ча с несопряженными профилями работать не может. Для несопряженных профилей профиль р^ 8 49
зуба второго колеса не обя­зательно эвольвентныЁ. Вы­полним его также круговым, но вогнутым, с г2, несколько

БоЛЬШИМ, НО блИЗКИМ К Т

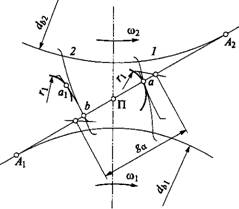
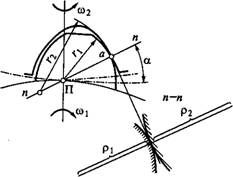
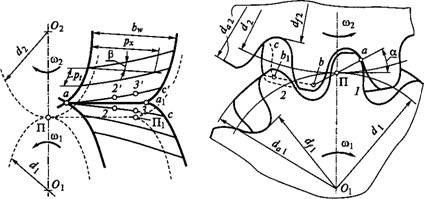
(рис. 8.51). Контактные на­пряжения значительно уме­ньшаются, так как контакт выпуклых эвольвентных про­филей заменен контактом выпуклого и вогнутого про­филей с малой разностью радиусов кривизны. Для со­хранения непрерывности за­цепления передачи Новикова выполняют косозубыми с 8р> 1. В сечении плоскостью п — п (рис. 8.51) боковые поверхности косых зубьев имеют большие радиусы кривизны рх и р2 винтовых линий. При вращении колес косые зубья перекатываются в плоскости п — п как цилиндры. Точка контакта а перемещается вдоль зубьев от одного края к дру­гому. Процесс такого зацепления иллюстрируется рис. 8.52, изоб­раженным в косоугольной проекции. Штриховой линией изображе­ны начальные цилиндры Dx и D2. Линия касания цилиндров ПП] — полюсная линия. Контурными линиями изображены цилиндры, проходящие через точку а контакта зубьев (см. рис. 8.50 и 8.51). Эти цилиндры пересекают поверхности зубьев по винтовым линиям ас, ас' и т. д. При указанном направлении вращения точка контакта винтовых линий, а следовательно, и точка контакта зубьев переме­щаются по линии аах. В контакт последовательно вступают точки 2 и 2 3 и 3' и т. д.

Рис. 8.50

Так как во всех попереч­ных сечениях форма зубьев не изменяется, то расстояние точек контакта от полюсной линии ПП! остается посто­янным. Это означает, что ли­ния аах прямая, параллель­ная полюсной линии. Линия аах является линией зацепле­ния в передачах Новикова. Ее длина равна ширине колеса BW9 а коэффициент перекры­тия [см. формулу (8.23)] р^ 8 51

Ч = bw/Px = (bw Sin P)lpn=(bw Sin P)/(nm„),

Где px — осевой шаг.

Если линия зацепления располагается за полюсной линией (по направлению вращения ведущего колеса; рис. 8.51), то зацепление называют заполюсным, если до полюса — дополюсным (рис. 8.52). Одна и та же пара колес может иметь заполюсное или дополюс - ное зацепление в зависимости от того, какое из них является веду­щим.

Признаком заполюсного зацепления является выпуклый про­филь у ведущего зуба и вогнутый у ведомого; дополюсного — вог­нутый у ведущего и выпуклый у ведомого. Очевидно, можно выпол­нить зубья так, чтобы одна часть их профиля была выпуклой, а другая — вогнутой. Тогда они смогут зацепляться и за полюсом, и до полюса. Так был разработан вариант дозаполюсного зацепле­ния (рис. 8.53).

(8.92)

Рис. 8.53

Рис. 8.52

Дозаполюсное зацепление имеет две линии зацепления, про­ходящие через точки а и Ь. Соответственно в два раза увеличивается и число точек контакта зубьев. В таких передачах зубья шестерни и колеса имеют одинаковый профиль: выпуклый — у головки, вогнутый — у ножки. На рис. 8.53 изображен момент, когда первая пара зубьев соприкасается в точке а, расположенной в пе­редней торцовой плоскости. При этом головка зуба шестерни соприкасается с ножкой зуба колеса. У второй пары зубьев в передней торцовой плоскости наблюдается зазор. В этот момент контакт второй пары зубьев (в данном случае) осуществляется в точке Ьи расположенной в другой торцовой плоскости, сме­щенной относительно первой на отрезок ЬЬХ. Линия Ьхс пересечения этой плоскости с боковой поверхностью зуба колеса изображена
штриховой линией. В точке Ь ножка зуба шестерни соприкасается с головкой зуба колеса; ЬЬ — линии зацепления второй пары зубьев. По стандарту обе линии зацепления, аа и ЬЬи расположены в одной плоскости с полюсной линией ППЬ

Сравнивая два варианта зацепления с одной (см. рис. 8.51) и двумя (рис. 8.53) линиями зацепления, отметим следующее. При одной линии зацепления у шестерни и колеса разные профили зубьев. Для их нарезания необходимо два различных инструмента (два исходных контура). При двух линиях зацепления зубья шестер­ни и колеса можно нарезать одним инструментом (один исходный контур). Очевидно, что нагрузочная способность передачи с двумя линиями зацепления больше, чем с одной. Поэтому дозаполюсное зацепление считают предпочтительным. С зацеплением Новикова изготовляют передачи не только цилиндрические, но и конические

[25].

Оценка передачи. Основное достоинство передачи Новикова — повышенная нагрузочная способность по контактной прочности. При #<350 НВ она примерно в 1,5...1,7 раза больше, чем у ана­логичной по размерам и материалу эвольвентной косозубой пере­дачи.

Недостатки — повышенная чувствительность к изменению меж­осевого расстояния; сравнительно сложный исходный контур инст­румента (см. ГОСТ 15023 — 76); некоторое снижение изломной прочности по сравнению с эвольвентным профилем.

(8.93)

Основные геометрические параметры. Колеса передачи Новикова нарезают обычно без смещения:

D=mxz; da=d+2m„h*; df=d-2me(h*+c*);

А=0,5Mt (zx + z2); mt=MnjCos /?

Обозначения те же, что и для эвольвентных передач: /?=10...22°, А* = 0,9, с* = 0,15.

Критерии работоспособности и расчета. Без учета деформаций и приработки контакт зубьев в передаче Новикова осуществляется в точке, а не по линии, как у эвольвентных передач. Однако малая разность радиусов кривизны гх и г2 выпуклых и вогнутых поверх­ностей зубьев, а также большие радиусы кривизны рх и р2 косых зубьев в плоскости п — п (см. рис. 8.51) приводят к тому, что под нагрузкой точечный контакт переходит в контакт по пятну — рис. 8.54, а для заполюсного зацепления и рис. 8.54, б для дозаполюс - ного зацепления. В последнем случае будет два пятна контакта, соответствующие двум линиям зацепления. В соответствии с рис.

8.53 два пятна контакта в точках а и Ь располагаются на двух соседних зубьях. На рис. 8.54, б пятно контакта второго зуба изображено штриховой ли­нией. Площади пятен контакта, а следо­вательно, и нагрузочная способность по контактным напряжениям у передач Но­викова больше, чем у эвольвентных.

Точечный, а не линейный контакт приводит к понижению изломной проч­ности. Например, у прямозубой эволь - вентной передачи нагрузка теоретически распределена по всей длине зуба и изло­му сопротивляется все сечение зуба у его основания. У заполюсной передачи Но­викова без учета контактных деформаций нагрузка сосредоточена в точке. При этом опасно зацепление вблизи торцов, когда выламы­ваются края зубьев. Поэтому рекомендуют выполнять коэффициент осевого перекрытия при котором по краям зубьев обес­

Печивается двухпарное зацепление.

Смещение линии зацепления и точки контакта от полюса приво­дит к скольжению в торцовой плоскости (см. § 8.2) со скоростью Vs=E(Coi + Co2% где е равно отрезку Па (см. рис. 8.53).

(8.94)

В осевом направлении зубья не скользят, а перекатываются по линиям зацепления подобно двум цилиндрам с радиусами рх и р2. Скорость качения

V* = V(px/pt) = V Ctgft

Где V — окружная скорость.

Для распространенных величин /? скорость vx значительно боль­ше v, что благоприятно для образования режима жидкостного трения. Благоприятные условия смазки приводят к увеличению КПД и уменьшению износа зубьев.

Точечный (теоретический) контакт делает передачи Новикова менее чувствительными к перекосам, чем передачи с линейным контактом. Зато они более чувствительны к изменению межосевого расстояния. Таким образом, основным критерием работоспособно­сти и расчета передач Новикова является прочность по контакт­ным и изгибным напряжениям.

Способы повышения прочности. 1. Увеличение числа пятен кон­такта путем применения дозаполюсного зацепления и увеличе­ния коэффициента перекрытия Для дозаполюсных передач при­меняют 1,3 или 2,3. Наиболее распространены efi= 1,3...1,4,
так как при увеличении увеличивается Bw [см. формулу (8.92)]. При больших Bw требуются повышенная точность и жесткость.

2. Увеличение площади пятен контакта (рис. 8.54) путем умень­шения разности г и г2 (см. рис. 8.51) и увеличения р и р2. На практике принимают r2«(l,2...1,3)ri. Радиусы кривизны рх и р2 уве­личиваются с уменьшением /?. С учетом противоположного влияния Р на вр и р рекомендуют /?=8...25°.

3. Применение колес с малым числом зубьев, что при одном и том же диаметре (D—Mz) равнозначно увеличению т и, следовательно, одновременному повышению прочности как по напряжениям изги­ба, так и по контактным напряжениям [см. формулы (8.95) и (8.96)]. Рекомендуют zi= 13...20.

Материалы. Для передач Новикова применяют те же материалы, что и для эвольвентных (см. табл. 8.7). Наиболее распространены материалы с твердостью рабочих поверхностей ^ 350 НВ. Напом­ним (см. § 8.11), что применение материалов с высокой твердостью поверхности (цементация, ТВЧ, азотирование и пр.) в эвольвентных передачах направлено в основном на повышение контактной про­чности и сближение ее с прочностью по изгибу. В передачах Нови­кова такое сближение достигается путем существенного увеличения площади пятен контакта. Поэтому применение материалов с высо­кой твердостью поверхности здесь менее эффективно. Уменьшая способность к приработке, они не приводят к существенному повы­шению нагрузочной способности. Ограничением становится про­чность по изгибу.

В передачах Новикова целесообразно применять, например, объ­емную закалку. Однако она сопровождается короблением и требует последующего шлифования зубьев. При сложном профиле зубьев эта операция встречает существенные затруднения.

Расчет на прочность. Условия контакта зубьев в передачах Но­викова существенно отличаются от условий контакта по Герцу (малая разность гх и г2, большие р и р2). Размеры площадок контакта здесь соизмеримы с размерами зубьев, а контактные напряжения приближаются к напряжениям смятия (удельным дав­лениям). Поэтому расчет передач Новикова по контактным нап­ряжениям, определяемым по зависимостям Герца, применяют условно.

Определение удельной нагрузки Q и приведенного радиуса кри­визны Рпр для зацепления Новикова значительно сложнее и здесь не рассматриваются.

Ниже приведены (без вывода) основные расчетные зависимости для цилиндрических передач дозаполюсного зацепления по ГОСТ 15023 — 76*:

'"Здесь и далее даны формулы из [25] с небольшими преобразованиями.

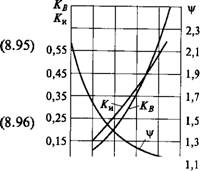
Где Ј„p, Г,, 2i, u9 KHv9 KFv9 mn9 09 [aH]9 0,05^ 10 2o 30 40^ [aF] то же, что и для эвольвентных пере - ................................. р, Дач; — целая часть величины е^ (напри­мер, при ер= 1,3 1); Кв, ЛГИ — коэффи­циенты, зависящие от угла /? (рис. 8.55); j/ — коэффициент, зависящий от Ае=ер—ер (рис. 8.55); YF — коэф­фициент формы зуба, определяемый в зависимости от эквивалент­ного числа зубьев Zv=Z/Cos3 /?:

О 0,1 0,2 0,3 0,4 Де Рис. 8.55

По контактным напряжениям

4 = 0,62 ./W^O*').

/10 напряжениям изгиба ТХКМ

OF=

Mlzi EPYF

........... 12 13 14 15 16 17 18 19 20 21 24 26

YF........ 0,87 0,89 0,92 0,93 0,95 0,96 097 0,98 0,99 1,0 1,03 1,04

В отличие от эвольвентных передач контактная прочность пере­дач с зацеплением Новикова зависит от числа зубьев Z или при постоянном D от модуля /я.

Пример расчета 8.4. В передаче из примера 8.1 (см. рис. 8.43) заменить эвольвент - ное зацепление второй ступени зацеплением Новикова и сравнить размеры.

Расчет. Материал и допускаемые напряжения сохраняем: =509 МПа; для шестерни |>^=278 МПа; « = 3,33; 7i=234 103 Н мм; л1 = 158,2 мин"1.

1. Определяем d по формуле (8.95). По рекомендациям (см. выше) предваритель­но назначаем /?=14°, £^=1,3, ^ = 15. По графику (рис. 8.55) находим Кв=0,14. По табл. 8.3 /£#„ = 1,05 (см. пример 8.1).

/2,1 • 105 * 1=0,62 у

Подставляя данные в формулу (8.95), с учетом £^=1, находим '

234 103 '1,05 0,14 15 (3,33 + 1)

------ = 51,118 мм.

5092 • 1 • 3,33 cos 14°

Модуль тп =d cos P/z = 51,118 • 0,97/15=3,3 мм. По табл. 8.1 принимаем т„=3,5 мм. При этом 4=3,5' 15/0,97 = 54,124 мм.

2. По формуле (8.96) проверяем прочность по напряжениям изгиба. Предварите­льно принимаем KFv=Kffv = 1,05; по рис. 8.55 /£„=0,2 и при Д8=Ер—£^=0,3 ф = 1,25. Далее zvl =zx/Cos3 Р=15/cos314° = 15 • 0,9135 = 16,42 и 0,955. При этом

234 103 -1,05 0,2 1,25

AF=----------------------------- = 76,93 МПа <М=278 МПа.

З,53 -15 1,3 0,955

Условие прочности соблюдается. Отмечаем, что в нашем примере нагрузка передачи ограничивается контактной прочностью.

3. Определяем ширину колес по формуле (8.92): Bw = е0тстп/Sin р= 1,3 я х х 3,5/sin 14°«59 мм. Число зубьев колеса z2=zи = 15'3,33^50. Диаметр колеса D2Z2' Mjcos Р=50 • 3,5/cos 14° = 180,357 мм.

В заключение сравниваем передачи:

Передача Новикова ^1 = 54,124 мм i/2 = 180,357 мм Bw = 59 мм

Отмечаем существенное уменьшение габаритов.