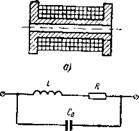
Катушка первичного элемента индуктивно-частотного преобра­зователя (рис. 2-1,а) представляет собой многослойный соленоид, намотанный на немагнитный каркас Материал каркаса должен иметь малую диэлектрическую проницаемость, низкие потери на высоких частотах и низкий температурный коэффициент расшире­ния. Такими свойствами обладают, например, фторопласт и высоко­частотный текстолит. Важнейшими электрическими параметрами катуш­ки являются индуктивность L0, ак­тивное сопротивление Ro и собствен - ная емкость С0.

РІндуктивность катушки. Индук­тивность любого контура с током определяется отношением потоко - сцепления контура к его току:

Если полный магнитный поток, сцепляющийся с коетуром, обуслов­лен токами, протекающими в других контурах, вводится понятие коэффи­циента взаимоиндукции:

4?k

М, к = т - (2-2)

Катушку датчика следует рассматривать как сложный контур. Непосредственное применение выражений (2-1) и (2-2) для расчета ее индуктивности весьма затруднительно.

Для упрощения расчетов катушку прямоугольного сечения мож­но заменить массивным витком такой же формы и размеров. Тогда

L0 = w2LB,

где w — число витков катушки; LB — индуктивность соответствующего массивного витка.

Конкретные выражения для индуктивности катушек различных поперечных сечений имеются в специальной литературе [Л. 8, 10, 12]. Они получены в результате введения некоторых допущений, кото­рые приводят к весьма незначительным погрешностям. К принятым допущениям относятся:

1) пренебрежение спиральностью витков (катушка рассматри­вается как совокупность отдельных замкнутых плоских витков, ле­жащих в нескольких параллельных плоскостях);

2) равномерное распределение тока по сечению отдельных вит­ков;

3) бесконечно тонкая изоляция и плотное заполнение витками всего пространства, занятого обмоткой.

Для особо точных расчетов можно воспользоваться выраже­ниями для поправок на изоляцию и частоту.

С учетом перечисленных допущений индуктивность катушки, показанной на рис. 2-1,а, составит [Л. 10]:

L° = it тЧ"ф /к^к)* <2'3)

где Цо — абсолютная магнитная проницаемость воздуха;

1*у — соответственно длина, средний диаметр и толщина

обмотки, м.

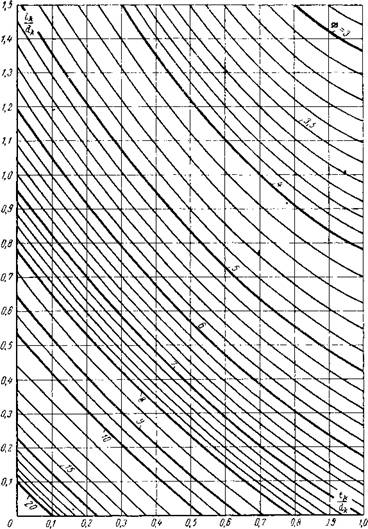
Значения Ф для различных tK/dK и lKfdK находятся из графи­ков. На рис. 2-2 даны кривые для определения Ф коротких ка­тушек.

Активное сопротивление катушки определяется из выражения

R°= ys” *

где /, 5 — длина и площадь поперечного сечения провода, м, м2

Y — удельная проводимость материала (1 /ом-м).

При повышении рабочей частоты активное сопротивление суще­ственно возрастает за счет поверхностного эффекта, эффекта близо­сти и диэлектрических потерь в изоляции витков. Поверхностный эффект проявляется в неравномерном распределении тока по сече­нию провода, что вызывает уменьшение его эффективного сечения. Эффект близости заключается в изменении распределения тока в проводнике под влиянием магнитного потока соседних провод­ников.

Прирост активного сопротивления по этим двум причинам со­ставляет:

/ wan 2 1

F W + ) G (ka) - 1J, (2-5)

где F(ka) и G(ka) — коэффициенты, выражающиеся через функции Бесселя от аргумента ka (табл. 2-1);

а — радиус провода, м k=Y

ji— магнитная проницаемость материала провода; ^нар — наружный диаметр катушки, м п — поправочный коэффициент [Л. 13]. Сопротивление диэлектрических потерь в катушке обусловлено в основном потерями в изоляции витков и зависит также от соб­ственной емкости катушки С0.

При-работе на частотах, значительно отличающихся от резо­нансной частоты катушки (практически при /^0,3/рез), потерями изгза влияния собственной емкости катушки можно пренебречь.

Собственная межвитковая емкость катушки для многослойных катушек С0 достигает существенной величины, и с ней приходится считаться. При обыкновенной намотке С0 колеблется в пределах 40—70 пф.

■ Если рабочая частота ниже частоты собственного резонанса ка­тушки, то на схеме замещения С0 изображается емкостью, включен­ной параллельно индуктивности и активному сопротивлению катуш­ки