Коэффициенты отражения и про­зрачности. При падении упругих волн на границу раздела двух сред волны частично проходят во вторую среду, а частично от­ражаются. Коэффициент отражения R определяется как отношение амплитуды Дотр отраженной волны к амплитуде Дпад падающей волны:

R = А / л

і -^отр' лпад*

Коэффициент прозрачности D — это отношение амплитуд прошедшей А„р и падающей волн:

Г9 Дпр/Дпад*

Подобными формулами определяют­ся также коэффициенты отражения и про­зрачности по энергии. Вместо амплитуд в формулы входят значения энергий или интенсивностей волн.

При нормальном падении волны (рис. 1.16, а) коэффициенты отражения и прозрачности (для амплитуд колебаний) равны

R = (z' - z)(z' + z); D = 2z'/(z' + z)

(1.12)

где z! и z' - волновые сопротивления пер­вой и второй сред, чаще всего - акустиче­ской задержки (призмы, иммерсионной жидкости) и изделия. При УЗ-контроле обычно передают волны из задержки в изделие, а затем (в ходе приема) - из изде­лия в задержку. В результате волна пере­ходит границу задержка ■*- изделие дваж­ды: в прямом и обратном направлениях. Коэффициент прозрачности в прямом и обратном направлениях

D = 4zz' /(z + z'f.

Именно этот коэффициент прозрач­ности важен для УЗ-контроля. Он же - коэффициент прозрачности по энергии.

а) б) в)

Рис. 1.16. Отражение, преломление и трансформация волн при падении продольной волны на границу оргстекло - сталь: сплошные линии - продольная волна, штриховые - поперечная волна, волнистая - поверхностная волна

Заметим, что 7?2 - коэффициент отражения по энергии и в соответствии с законом сохранения энергии R2 + D = 1.

Чем больше разница (или отношение) волновых сопротивлений сред, тем мень­ше доля прошедшей энергии и больше отраженной. Например, при нормальном падении продольной волны на границу сталь - воздух (или воздух - сталь) прохо­дит только 0,002 % энергии, через границу вода - сталь ~12 % энергии, а через грани­цу оргстекло - сталь проходит 25 % (от­ражается 75 %). Это объясняется тем, что волновое сопротивление воды больше, чем воздуха, а у оргстекла еще больше. Они последовательно приближаются к волновому сопротивлению стали.

При нормальном падении волны из среды с большим волновым сопротивле­нием на границу со средой с малым вол­новым сопротивлением коэффициент от­
ражения, согласно формуле (1.12), отрица­телен. Это означает, что фаза волны изме­няется на обратное значение. Например, на границе твердое тело - воздух (вакуум) R = -1. Фаза отраженной волны обратна по отношению к фазе падающей волны, и в результате сложения волн выполняется условие равенства нулю напряжений на свободной поверхности. Это можно заме­тить по изменению фазы первого полупе - риода.

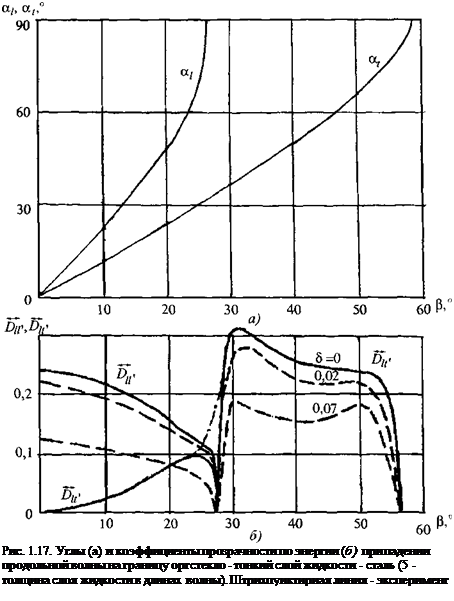
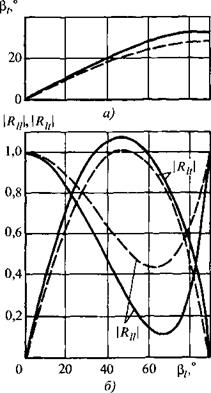
Величины коэффициентов отражения и прозрачности при наклонном падении выражаются более сложными формулами, чем при нормальном. Для границ оргстек­ло - сталь графики коэффициентов про­зрачности приведены на рис. 1.17, а вода - сталь - на рис. 1.18.

Направление распространения волн. Если нижняя и верхняя среды - твердое тело, то в них при падении упру­гой волны на границу возникает сразу две

волны: продольная и поперечная (см. рис. 1.16, б). Явление превращения одного ти­па волн в другой называют трансформа­цией волн. Если какая-либо среда - жидкость или газ, то поперечные волны в ней отсутствуют. Направление отражен­ных и преломленных, продольных и попе­речных волн определяется законом сину­сов (законом Снеллиуса):

sin(3 _ siny; _ sin у, _ sina; _ sina, _ congt C Cf с, с} c

(1.13)

Обозначения углов показаны на рис. 1.16, б; с, ct, c,, c, c - скорости волн падающей, отраженной продольной, от­раженной поперечной, преломленной про-

дольной, преломленной поперечной. Та­ким образом, для всех волн отношение синуса угла (между направлением волны и нормалью к поверхности раздела) к скоро­сти волны будет постоянной величиной.

При УЗ-контроле чаще всего встре­чается случай, когда падает продольная волна, а в результате преломления и трансформации возникают продольная и поперечная волны, причем скорости обеих

волн больше, чем скорость с падающей волны (см. рис. 1.16, б). Возникают также отраженные волны: продольная, если

верхняя среда жидкая; продольная и попе­речная, если верхняя среда твердая.

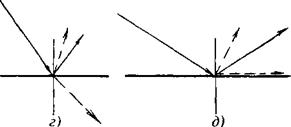
Если увеличивать угол падения, то при некотором его значении угол прелом­ления для продольной волны будет равен 90° (см. рис. 1.16, в). Преломленная про­дольная волна будет распространяться

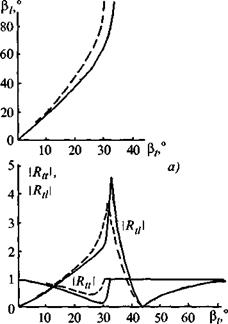
Рис. 1.19. Углы (а) и коэффициенты (б) отражения по амплитуде от границ сталь - воздух (---- ) и алюминий-воздух (- ) при падении продольной волны

вдоль поверхности (в акустике такую вол­ну называют неоднородной). Она как бы станет головной волной. Этот угол паде­ния называют первым критическим. При еще больших углах падения (см. рис. 1.16, г) во второй среде останется только попе­речная волна. При втором критическом угле (см. рис. 1.16, д) поперечная волна пойдет вдоль поверхности, т. е. обе пре­ломленные волны испытают полное внут­реннее отражение. Критические углы рас­считывают по формуле

(3 = arcsin(c / с'),

где с' - скорость продольной или попе­речной преломленной волны.

Как отмечалось в разд. 1.1.3, наибо­лее распространенный способ возбужде­ния поперечных волн в изделии - с помо­щью преобразователя с призмой, угол ко­торой лежит между первым и вторым кри­тическими углами (см. табл. 1.2). Для гра­ницы органическое стекло (плексиглас) - сталь первый критический угол падения продольной волны в плексигласе равен 27,5°. При этом угол преломления для продольной волны 90°, а для поперечной а, = 32°. Второй критический угол (3 = (3" =

= 57,5°. При этом угле падения возбужда­ется поперечная головная волна, но заме­тить ее крайне трудно. При угле, несколь­ко большем второго критического (см. рис. 1.16, е),

(3S = arcsin(c / cs)

возникает поверхностная рэлеевская волна со скоростью cs. Для границы оргстекло - сталь угол падения, при котором возбуж­дается эта волна, равен (3S = 65°. Подоб­ным способом возбуждаются также нор­мальные волны (см. разд. 1.1.2).

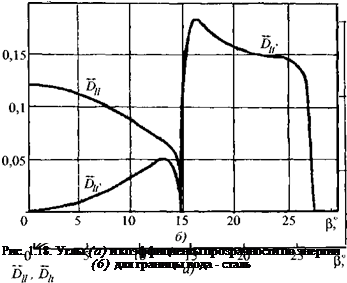
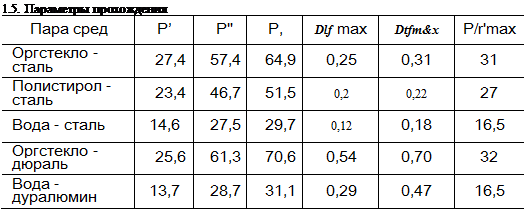
Графики изменения углов преломле­ния и коэффициентов прозрачности в за­висимости от угла падения для границ оргстекло - сталь и вода - сталь показаны на рис. 1.17 и 1.18. В табл. 1.5 примени­тельно к некоторым парам сред приведе­ны углы (3', (3" и (3S (в градусах), макси­мальные значения коэффициентов про­зрачности (по энергии) при образовании продольных DIVmax и поперечных Dlt'шах волн, углы (3/('тах (в градусах), при кото­рых достигается максимальная величина коэффициента прозрачности для попереч­ных волн.

Колебания частиц в поперечных вол­нах, возникающих в результате трансфор­мации из продольной волны, происходят в той же плоскости, что и в продольной волне, - в плоскости падения, т. е. в плос­кости, показанной на рис. 1.16. Как отме­чалось, такую поперечную волну называ­ют волной с вертикальной поляризацией.

Поперечную волну с горизонтальной по­ляризацией можно возбудить преобразо­вателями специального типа, например ЭМА.

Граница твердого тела. Когда рас­пространяющаяся в твердом теле про­дольная или поперечная вертикально по­ляризованная волна падает на его поверх­ность, возникают две отраженные волны: продольная и поперечная. Рассчитанные значения углов и коэффициентов отраже­ния (по амплитуде) для продольной волны в стали и алюминии показаны на рис. 1.19, а для вертикально поляризованной попе­речной волны - на рис. 1.20. При падении на поверхность поперечной волны суще­ствует третий критический угол. При нем продольная отраженная волна сливается с поверхностью (становится неоднородной) и отражается одна поперечная волна. Для стали этот угол Р = ср'=33°, для дуралю - мина-29,5°.

Угол, соответствующий наибольшей трансформации (точнее, минимальному коэффициенту отражения без трансфор­мации), называется квазиобменным. При нем большая часть энергии волны транс­формируется в волну другого типа. Тер­мин "обменный угол" (без "квази") ис­пользуется, если трансформация мод про­исходит полностью. Для стали при паде­нии продольной волны квазиобменный угол р; = 68°. При нем амплитуда отра­женной продольной волны минимальна.

Амплитуда отраженной трансформиро­ванной поперечной волны достигает мак­симума при меньшем угле падения (46°). При падении поперечной волны (см. рис. 1.19, б) квазиобменный угол р, = 33°. Для дуралюмина квазиобменные углы Р, =63,5° и р,= 29°.

б) Рис. 1.20. Углы (а) и коэффициенты (6) отражения по амплитуде от границ сталь - воздух (---- ) и алюминий-воздух (- ) при падении поперечной волны

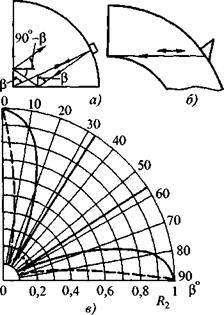
Рис. 1.21. Схема отражения от двугранного угла с плоскими гранями (а) и от двугранного угла с одной плоской и одной цилиндрической гранями (6); коэффициент двойного отражения в стали для продольных (- ) и поперечных (----- ) волн

При отражении горизонтально поля­ризованной поперечной волны трансфор­мация не возникает, если отражающая плоскость совпадает с плоскостью поля­ризации, т. е. горизонтальна. Если отра­жающая плоскость не совпадает с плоско­стью поляризации горизонтально поляри­зованной волны или она не перпендику­лярна к плоскости поляризации попереч­ной волны, то в отраженной волне будут как вертикальная, так и горизонтальная составляющие, причем каждая состав­ляющая отражается по присущим ей зако­нам [350]. Подобная ситуация иногда воз­никает при контроле способом тандем - дуэт (см. разд. 2.2.5.1).

На рис. 1.21, а, б, в показаны двойное отражение от прямого двугранного угла и коэффициент такого отражения:

Д2 = Я(Р)Я(9 0°-Р).

В результате двойного отражения не- трансформированный эхосигнал возвра­щается к излучающему преобразователю (угловой эффект). На практике двойное отражение часто встречается для попереч­ных волн. При углах [3, в интервале между ср' и (90° - ср') (для стали 33 ... 57°, для дуралюмина 29,5 ... 60,5°) такая волна отражается без трансформации, поскольку для обеих граней углы падения больше третьего критического.

Для продольных волн такой случай отражения сравнительно редок. Если про­дольная волна распространяется вдоль свободной поверхности, она является го­ловной, порождает поперечную волну и быстро ослабляется. Поэтому при |3 = 0 и 90° коэффициент отражения R = 1, как показано на рис. 1.21, а, только тогда, ко­гда грань угла, вблизи которой распро­страняется продольная волна, имеет кри­волинейную форму (рис. 1.21, б). Такая ситуация возникает при контроле объек­тов с цилиндрической внутренней по­верхностью, например толстостенной тру­бы или вала с центральным каналом.

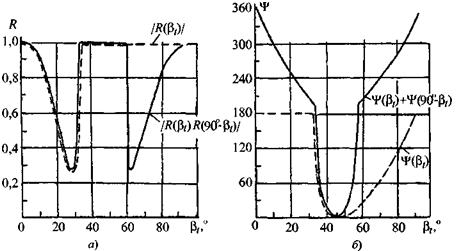
На рис. 1.22, а для поперечной волны в стали в декартовых координатах показа­ны модуль коэффициента отражения по­перечной волны и коэффициент двойного отражения от прямого двугранного угла (повторно), а на рис. 1.22, б - изменение фазы отраженной волны при однократном и двойном отражении. Как видно, вблизи третьего критического угла ср' (больше его) фаза отраженной волны изменяется на значительную величину, не кратную л.

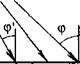
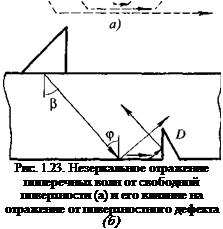
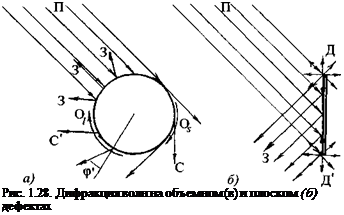
Это вызывает явление незеркального отражения: происходит смещение отра­женных лучей вдоль поверхности (рис. 1.23, а). Точка отражения луча не совпада­ет с точкой падения. Это тем заметнее, чем угол падения ср = [3 ближе к ср' и чем ниже частота. Оно подробнее будет рас­смотрено ниже. На рис. 1.23, б показано, что лучи, которые по законам геометриче­ского отражения не должны были отра­зиться от дефекта D, в результате незер­кального отражения испытают отражение от него.

При ф —> ср' величина смещения Д возрастает до бесконечности. Это соответ­ствует возникновению головной волны. Явления нарушения геометрических зако­нов отражения и преломления наблюда­ются не только на свободной поверхности, но и на границе двух протяженных сред при углах падения, близких к критиче­ским.

Граница сред, разделенных тонким слоем. Если волны проходят из одной протяженной твердой среды в другую че­рез зазор, заполненный воздухом, то про­хождение очень плохое, потому что вол­новое сопротивление газа в тысячи раз меньше, чем твердых тел. Это способству­ет хорошему обнаружению очень тонких несплошностей (дефектов) в твердом теле: УЗ-волны от них практически полностью отражаются. Но это же затрудняет переда­чу УЗ-волны от преобразователя в ОК, поэтому промежуток между ними запол­няют контактной жидкостью.

Очень тонкий промежуточный слой контактной жидкости слабо влияет на ко­эффициенты отражения и прозрачности.

Значения коэффициентов прозрачно­сти, показанные на рис. 1.17 сплошными
кривыми, а также приведенные в табл. 1.4, соответствуют варианту, когда между призмой преобразователя и ОК имеется очень тонкий слой контактной жидкости: 8 = h/Xc —> 0 , где h - толщина слоя, а дс - длина волны в нем. Такой слой позволяет ввести граничное условие, чтотангенци-

б)

альные напряжения на поверхностях призмы преобразователя и ОК равны ну­лю. Увеличение толщины слоя (при со­блюдении условия 5 «1) ухудшает про­хождение (см. рис. 1.17).

При увеличении толщины слоя, со­измеримом с длиной волны, амплитуды прошедших и отраженных волн имеют максимумы и минимумы. При нормаль­ном падении, если волновое сопротивле­ние слоя zc меньше (или больше), чем обе­их протяженных сред z и z', то коэффици­ент отражения больше или равен R в от­сутствие слоя. Однако прохождение улучшается, если zc лежит в интервале между z и z'. Это явление называют про­
светлением границы. Максимальная про­зрачность, т. е. D = 1, достигается при ус­ловиях

h = c/4 zc=V^.

Строго говоря, приведенное соотно­шение справедливо для гармонических колебаний, причем значение D = 1 дости­гается, если просветляющий слой не имеет потерь. Уменьшение числа периодов УЗ - импульса и увеличение потерь в слое ухудшают согласование (уменьшают зна­чение D), однако и в этом случае наблю­дается максимум прозрачности слоя.

Если обе протяженные среды одина­ковы, а слой тонкий (h«Xc), то коэффи­циент отражения по энергии при нормаль­ном падении

-і

(1Л4)

В табл. 1.6 сведены рассчитанные по формулам (1.12) и (1.14) значения R2 для слоев в стали, частота 2,5 МГц. Таблица показывает практически полное отраже­ние от тончайшего воздушного зазора (0,00001 мм), имитирующего дефект. Заполнение зазора жидкостью резко улуч­шает прохождение.

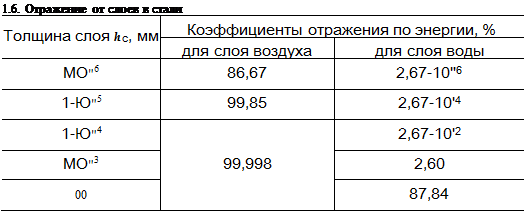Экспериментальные исследования (рис. 1.24) не подтверждают расчетных результатов по отражению от тонкого воз-

душного зазора [350]. Коэффициенты от­ражения начинают заметно уменьшаться по сравнению с единицей (а прозрачность увеличиваться)при hc =2 ■ 104 ... 1 • 10'2 мм по измерениям, проведенным разными авторами.

Отражение и преломление импуль­сов и пучков лучей. Приведенные выше сведения об отражении и прохождении волн относятся к непрерывным колебани­ям и волне с плоским фронтом. Далее рас­сматриваются изменения, происходящие при отражении импульсов, и варианты отражения пучка параллельных лучей (плоская ограниченная волна) и веерооб­разно расходящегося от излучателя пучка лучей (квазисферическая волна). При этом амплитуда лучей в пределах пучка может изменяться. Первый вариант приближенно реализуется в непосредственной близости от плоского излучателя, а второй - в его дальней зоне (см. разд. 1.3).

Конечная длительность импульса уменьшает осцилляции коэффициентов R и D для границ, разделенных слоем. Сгла­живанию осцилляций способствуют также затухание УЗ в слое и уход волн из зоны соприкосновения сред при наклонном па­дении. По всем этим причинам для про­светления оптимален слой толщиной в 1/4 длины волны, а, например, не в 3/4 длины волны.

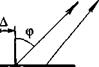
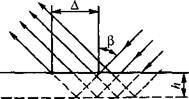
Рассмотренное выше явление незер­кального отражения теоретически обосно­вано [38, 39] для пучка параллельных лу­чей, падающих на границу (рис. 1.25). Точнее, в случае падения ограниченного пучка поперечных волн на свободную по­верхность твердого тела под углом ср, близким к третьему критическому углу ср' (для стали ср' = 33°), отраженная продоль­ная волна вырождается в неоднородную волну, обусловливающую быстрое изме­нение фазы колебаний, что эквивалентно смещению пучка вдоль поверхности. От­ражение пучка как бы происходит от мнимой границы (показана штриховой линией) на расстоянии h от действитель-

Рис. 1.25. Незеркальное отражение пучка параллельных лучей

ной. Набег фазы на пути 2kh/cos ср равен изменению фазы при отражении.

Кроме этого явления для поперечной волны происходит при угле падения на свободную поверхность, отличающемся от 45°, смещение отраженных лучей вследст­вие изменения фазы, которое показано на рис. 1.22, б. Смещение идет в двух на­правлениях. Для лучей с углом, меньшим 45°, пучок сдвигается вперед так же, как на рис. 1.25, а для лучей с углом, большим 45°, пучок смещается назад к преобразо­вателю. Предложена [161] приближенная формула для расчета смещения:

Здесь о - отклонение угла падения (в радианах) от 45°, к/ и к, - волновые числа для продольной и поперечной волн.

Отметим, что в формуле нет зависи­мости смещения от близости к критиче­скому углу, так как это явление при выво­де формулы не учитывалось. Оценки по­казывают, что в стали на частоте 2,5 МГц отклонение угла на +20° вызовет при от­ражении смещение пучка на 2,55 мм, а на частоте 1,8 МГц - на 3,55 мм.

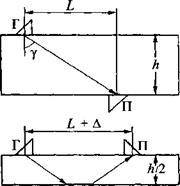
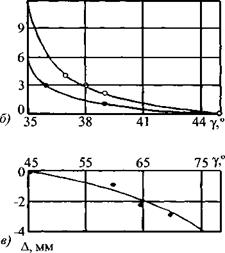
Явление смещения пучка лучей как при отклонении угла падения от 45°, так и в результате приближения угла падения к третьему критическому углу эксперимен­тально исследовано В. С. Гончаровым [91, 92]. Им продемонстрировано изменение смещения при вариации угла ср и частоты (рис. 1.26). Смещение Д вперед тем боль­ше, чем угол ср ближе к критическому и

а)

А, мм

Рис. 1.26. Схема (а) и результаты экспериментов по смещению пучка лучей при отражении от свободной поверхности стального ОК: ----- расчет по [38]; •, о - эксперимент на частотах 2,5 и 1,8 МГц; 6 - угол падения < 45°; в - угол падения > 45° к генератору Г и приемнику П

чем ниже частота. Например, для преобра­зователя на частоту 2,5 МГц с углом паде­ния на границу (равным углу преломле­ния) 37° смещение вперед составляет ~3 мм, а для угла падения 45° смещение А = 0. Для угла падения 65° (> 45°) смеще­ние назад ~2 мм. Это близко к приведен­ному выше теоретическому значению
смещения назад для угла преломления 65°, но не соответствует смещению вперед в области критического угла.

Отражение и преломление расходя­щегося пучка для каждого луча происхо­дят так же, как для плоской волны. В ре­зультате амплитуды лучей изменяются пропорционально значениям R и D для данного угла падения. Как для плоской волны, для каждого луча происходит сме­щение вдоль границы (см. рис. 1.23).

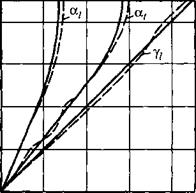
Изменение коэффициентов отраже­ния и прозрачности в зависимости от угла заметно влияет на положение максимума при отражении и прохождении расходя­щегося пучка лучей. На рис. 1.27 показано экспериментальное изменение углов пре­ломления ДЛЯ продольных (X/ и попереч­ных а, волн для границы оргстекло (приз­ма преобразователя) - сталь и угла отра­жения у/ продольных волн для границы сталь - воздух в результате изменения амплитуд лучей пропорционально значе­ниям R и D.

а,; “о У/

При экспериментах произведение диаметра пьезопластины на частоту соста­вило 30 мм-МГц. Видно, что значения уг­лов отражения и преломления отклоняют­ся от найденных по формуле синусов (1ЛЗ) в сторону максимумов значений R и

D. Явление тем сильнее, чем шире диа­грамма направленности преобразователя.

Экспериментально полученная кри­вая зависимости коэффициента прозрачно­сти от угла падения волны (см. рис. 1.17) удовлетворительно совпадает с теоретиче­ской. Исключение составляет область вблизи угла (З', где, согласно эксперимен­тальным измерениям, сглаживается выте­кающий из теории минимум коэффициен­та прозрачности Dlt (экспериментальное значение - штрихпунктирная линия на рис. 1.17). Это явление также объясняется отличием падающей волны от плоской и импульсным характером излучения.