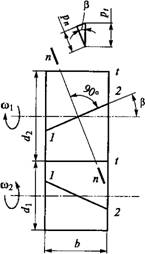
Геометрические параметры. У косозубых колес зубья располага­ются не по образующей делительного цилиндра, а составляют с ней некоторый угол /? (рис. 8.23, где а — косозубая передача; б — шев­ронная, и рис. 8.24). Оси колес при этом остаются параллельными. Для нарезания косых зубьев используют инструмент такого же исходного контура, как и для нарезания прямых. Поэтому профиль косого зуба в нормальном сечении п — п совпадает с профилем прямого зуба. Модуль в этом сечении должен быть также стандарт­ным (см. табл. 8.1).

В торцовом сечении / — t параметры косого зуба изменяются в зависимости от угла /?: окружной шаг pt=pn/cosfi, Окружной модуль mt=mn/cos/?, делительный диаметр d = mtz=Th^/Cos/?.

Индексы пи / приписывают параметрам в нормальном и тор­цовом сечениях соответственно.

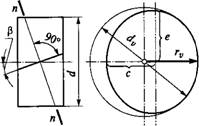
Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято опреде­лять через параметры эквивалентного прямозубого колеса (рис. 8.25).

Рис. 8.24

Нормальное к зубу сечение косозу - бого колеса образует эллипс с полуося­ми с = г и е=г/Cos/?, где r=d/2. В зацеп­лении участвуют зубья, расположенные

Рис. 8.23

На малой оси эллипса, так как второе колесо находится на расстоянии C = D/2. Радиус кривизны эллипса на малой оси (см. геометрию эллипса)

Rv = E2/C = R/ Cos2 /?.

В соответствии с этим форма косого зуба в нор­мальном сечении определя­ется эквивалентным прямо­зубым колесом, диаметр ко­торого

Dv=D/Cos2P (8.21)

И число зубьев

Zv = сЦтп = Dj{Mn Cos2 /?)=Mtz/(Mt Cos3 /?),

Или

Zv=z/cos30. (8.22)

Пример. При Р=20°, <4 = 1,134 Zv= 1,2Z.

Рис. 8.25

Увеличение эквивалентных параметров (Dv и Zv) с увеличением угла Fi является одной из причин повышения прочности косозубых пере­дач. Вследствие наклона зубьев получается колесо как бы боль­ших размеров или при той же нагрузке уменьшаются габариты передачи. Ниже показано, что косозубые передачи по сравнению с прямозубыми обладают еще и другими преимуществами: много - парность зацепления, уменьшение шума и пр. Поэтому в современ­ных передачах косозубые колеса получили преимущественное рас­пространение.

Многопарность и плавность зацепления. В отличие от прямых косые зубья входят в зацепление не сразу по всей длине, а постепен­но. Зацепление здесь распространяется в направлении от точек 1 к точкам 2 (см. рис. 8.24). Расположение контактных линий в поле косозубого зацепления изображено на рис. 8.26, а, б* (ср. с рис. 8.5 — прямозубое зацепление). При вращении колес линии контакта перемещаются в поле зацепления в направлении, показанном стрел­кой. В рассматриваемый момент времени в зацеплении находится три пары зубьев 7, 2 и 3. При этом пара 2 зацепляется по всей длине

♦Точнее, контактные линии расположены не под углом /?, а под углом Ft. Разность этих углов невелика, а ее влияние на а л не превышает 2%. Поэтому здесь и далее принимаем
Зубьев, а пары 7 и 5 — лишь частично. В следующий мо­мент времени пара 3 выхо­дит из зацепления и нахо­дится в положении 5'. Одна­ко в зацеплении еще оста­лись две пары 2 и Г. В от­личие от прямозубого косо - зубое зацепление не имеет зо­ны однопарного зацепления. В прямозубом зацеплении нагрузка с двух зубьев на один или с одного на два передается мгновенно. Это явление сопровождается ударами и шумом. В ко - созубых передачах зубья нагружаются постепенно по мере захода их в поле зацепления, а в зацеплении всегда находится минимум две пары. Плавность косозубого зацепления значительно понижает шум и дополнительные динамические нагрузки.

Отмеченное преимущество косозубого зацепления становится особенно значительным в быстроходных передачах, так как дина­мические нагрузки возрастают пропорционально квадрату скоро­сти.

(8.23)

Косозубые колеса могут работать без нарушения зацепления даже при коэффициенте торцового перекрытия еа<1, если обес­печено осевое перекрытие Bw>Pbt/Tgf} (рис. 8.26, б). Отношение

Fy = Bw tg P/Pbt« Bw sin/?/(7cm„)

Называют коэффициентом осевого перекрытия. Рекомендуют при­нимать е^ 1,1.

(8.24)

В косозубом зацеплении нагрузка распределяется на всю сум­марную длину контактных линий 7, 2, 5. Удельная нагрузка умень­шается с увеличением суммарной длины контактных линий /L. С по­мощью рис. 8.26 нетрудно установить, что при еа, равном целому числу,

K = BwEa/ Cos/?

И /L не изменяется при движении, так как уменьшению линий 3 всегда соответствует равное приращение линии 7. Точно так же постоянна при любом еа, но при е^, равном целому числу. Если отмеченные условия не соблюдаются, то k периодически изменяет­ся, а формула (8.24) будет определять среднюю величину, которую принимают за расчетную.

В соответствии с формулой (8.24) /z растет с увеличением /?, что выгодно. Однако во избежание больших осевых сил в зацеплении
(см. ниже) рекомендуют принимать /?=8...20°. Для шевронных ко­лес допускают /? до 30° и даже до 40°.

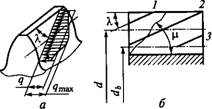
На боковой поверхности косого зуба линия контакта располага­ется под некоторым углом к (рис. 8.27, а). Угол X увеличивается с увеличением /?. По линии контакта нагрузка распределяется нерав­номерно. Ее максимум на средней линии зуба, так как при зацепле­нии серединами зубья обладают максимальной суммарной жест­костью.

При движении зуба в плоскости зацепления линия контакта перемещается в направлении от 7 к 5 (рис. 8.27, б). При этом опасным для прочности может оказаться положение 7, в котором у зуба отламывается угол. Трещина усталости образуется у корня зуба в месте концентрации напряжений и затем распространяется под некоторым углом ц. Вероятность косого излома отражается на прочности зубьев по напряжениям изгиба, а концентрация нагрузки Q — на прочности по контактным напряжениям.

С наклонным расположением контактной линии связана целесо­образность изготовления косозубой шестерни из материала, значи­тельно более прочного (высокотвердого), чем у колеса. Это объясня­ется следующим. Ножки зубьев обладают меньшей стойкостью против выкрашивания, чем головки, так как у них неблагоприятно сочетание направления скольжения и перекатывания зубьев (см. рис. 8.6 и 8.8). Следовательно, ножка зуба колеса, работающая с голов­кой зуба шестерни, начнет выкрашиваться в первую очередь. При этом вследствие наклона контактной линии нагрузка (полностью или частично) передается на головку зуба колеса, работающую с ножкой зуба шестерни. Слабая ножка зуба колеса разгружается, и выкрашивание прекращается. Дополнительная нагрузка ножки зуба шестерни не опасна, так как она изготовлена из более стойкого материала. Применение высокотвердой шестерни позволяет допол­нительно повысить нагрузочную способность косозубых передач на 25...30%.

Расчет коэффициента торцового перекрытия еа. Для нефланкиро - ванных передач без смещения (для других случаев см. ГОСТ 16532 — 70)

Еа=[0,95-1,6 (1/zi + l/z2)] (1 + cos/?) cos p. (8.25)

Знак «+» — для внешнего, а «—» — для внутреннего заце­пления. Для прямозубых пе­редач рекомендуют 1,2, для косозубых Величина еа за­висит от числа зубьев z и угла наклона зубьев р. С увеличени­ем z увеличивается еа. Поэтому
выгодно применять колеса с большими z или при заданном диамет­ре D колеса с малым модулем т. С увеличением /? растет окружной шаг ры, а рабочая длина линии зацепления Ga остается неизменной (см. выше). При этом еа уменьшается. Уменьшение еа является одной из причин ограничения больших /?.

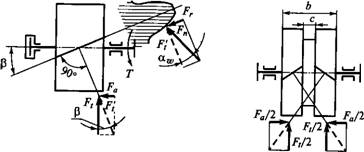
Силы в зацеплении. В косозубой передаче (рис. 8.28, а) нормаль­ную силу Fn раскладывают на три составляющие:

TOC o "1-3" h z окружную силу Ft=2Tldu - ч

Осевую силу Fa=Ft tg/?, I

Радиальную силу Fr=F[ tgaw=Ft tg^/cos/?, > (8.26)

В свою очередь, сила I

Fn=F'T/Cosoiw=/^/(cosan, cos^). J

Наличие в зацеплении осевых сил, которые дополнительно на­гружают опоры валов, является недостатком косозубых колес. Этот недостаток устраняется в шевронной передаче (см. рис. 8.28, б и 8.23), которая подобна сдвоенной косозубой передаче с проти­воположным направлением зубьев. Осевые силы здесь уравновеши­ваются на самом зубчатом колесе.

A

Расчет прочности зубьев по контактным напряжениям. Для косо­зубых передач удельная нагрузка с учетом формул (8.4), (8.24) и (8.26)

Q = FnKH/k = FtKHl(bvfia cosa).

По аналогии с прямозубым колесом, выражая в формуле (8.9) dwi через диаметр эквивалентного колеса dv [см. формулу (8.21)], получаем

Б

1 __ 2Cos Pup dw sinaw

Сравнивая отношение qjpup в формуле (8.7) для прямозубых [фор­мулы (8.8) и (8.9)] и косозубых колес, а также учитывая, что у по­следних отсутствует зона однопарного зацепления, находим

(?/Рпр)жос= (?/Рпр)прям (Cos2 Р)/еа

Или (8.27)

(<Гя)жос= (Ыфям ^/(СОЬ2Р)/ва.

Обозначим

ZH!=J(cos2P)/ea (8.28)

— коэффициент повышения прочности косозубых передач по кон­тактным напряжениям. В соответствии с формулой (8.10) для косо­зубых передач получаем

°н= 1.18 ZJ^F^i^M (8.29)

При проектном расчете /? и еа неизвестны. Поэтому величину ZHp в формуле (8.29) предварительно оценивают приближенно. При­няв в среднем /? = 12° и ва= 1,5,получаем 0,8, а формулы (8.11) и (8.13) проектного расчета путем умножения числовых коэффици­ентов на Vzg для косозубых передач запишем в виде

^-JWW}

Расчет прочности зубьев по напряжениям изгиба. Расчет выполня­ют по аналогии с прямозубыми передачами с учетом увеличения прочности косозубых передач (см. выше). При этом формулы (8.19) и (8.20) для косозубых передач записываются в виде: для проверочного расчета

>s2P /tt±l Ino*, И J

YFSYFliKFFtl(bjn„H[(TFl (8.32)

Для проектного расчета (принимая приближенно KFv& 1; см. табл. 8.3)

/я,=у/ 2TxKFaKFp YFSYFfi/(ZlIl/M [Gf]). (8.33)

Здесь YFp — коэффициент повьппения прочности косозубых передач по напряжениям изгиба:

(8.34)

Коэффициент перекрытия ва [см. формулу (8.25)] учитывает умень­шение нагрузки расчетного зуба ввиду многопарности зацепления. Yp=l— /?°/Ю0>0,7— коэффициент, учитывающий повышение из - гибной прочности вследствие наклона контактной линии к осно­ванию зуба и неравномерного распределения нагрузки (см. рис. 8.27). При этом равнодействующая нагрузки приближается к ос­нованию зуба, а изгибающий момент уменьшается. Формула для Yp получена на основании экспериментов. Коэффициент формы зуба Yfs выбирается по графику рис. 8.20, при эквивалентном числе зубьев Zv — по формуле (8.22), a Zu фт и /? выбирают по табл. 8.5, 8.6.