Квантовая теория гравитации (КТГ) базируется на идеи Эйнштейна искривления пространства-времени, которая в реалиях квантованной среды переходит в ее деформацию. При этом необходимо отметить, что гравитация начинается с элементарных частиц, а точнее, с формирования массы у элементарных частиц. При этом любая элементарная частица, в том числе, обладающая массой, - источником гравитационного поля, - представляет собой открытую квантомеханическую систему, являясь неразрывной частью квантованного пространства-времени.

Закрытых квантомеханических систем в природе не существует. Их придумали люди в силу ограниченности на том момент знаний о природе вещей. Это естественный путь познания явлений природы при исследовании наблюдаемых объектов и предметов. Нам кажется, что летящий камень представляет собой изолированный собственными размерами предмет как вещь в себе, не связанная, например, с Землей. Но камень все же падает на Землю, как яблоко Ньютона. Оказывается, что брошенный камень на самом деле не является изолированным от Земли объектом, находясь в тисках земного гравитационного поля, из которого очень трудно вырваться. Но для нас гравитационное поле является невидимым, и падающий камень кажется нам независимой замкнутой системой, вещью в себе.

Если бы мы могли видеть гравитационное поле, то увидели бы потрясающую картину. Гравитационное поле представилось бы нам в виде ауры окружающей летящий камень. Эта аура обусловлена деформацией квантованного пространства-времени вокруг камня. Такой же гравитационной аурой окружена Земля. Мы бы наблюдали, как аура Земли поглощает камень, пока на земной поверхности их ауры не сольются, обеспечивая повсеместное действие тяготения. Но это только внешняя сторона. Как отмечалось, гравитация начинается с элементарных частиц, входящих в состав всех тел, и в силу действия принципа суперпозиции полей, формируется суммарное гравитационное поле тела. Все элементарные частицы, а соответственно и все тела, представляют собой открытые квантомеханические системы.

Переход к открытым квантомеханическим системам в физике элементарных частиц и атомного ядра, позволяет подходить к проблемам квантовой механики уже с позиций объединения электромагнетизма и гравитации. Становится понятной структура элементарных частиц, которые на самом деле не столь элементарны и включают в свой состав громадное количество квантонов, определяя их квантованное состояние, благодаря которому возможно увеличение энергии и массы частицы с увеличением ее скорости. Переход к открытым квантомеханическим системам стал возможным только при возврате к научной концепции абсолютного квантованного пространства-времени. Это позволило установить структуру основных элементарных частиц: электрона, позитрона, протона, нейтрона, нейтрино, фотона, а также найти причину образования массы у элементарных частиц [5-17].

Чтобы связать структуру элементарных частиц и их массу со свойствами к деформации квантованного пространства-времени, исследуем процесс формирования массы у нуклонов. Но для этого необходимо было установить оболочечную структуру нуклона, оболочка которого способна сжимать квантованное пространство-время, формируя массу нуклона. Это возможно в том случае, если оболочка нуклона представляет собой сферическую сетку, в узлах которой размещены монопольные электрические заряды с чередованием полярности, формируя знакопеременную оболочку. При этом, независимо от наличия некомпенсированного заряда в оболочки протона, нуклону могут притягиваться между собой знакопеременными зарядами оболочек. Такие силы притяжения имеют чисто электрическую природу, являются короткодействующими, и по своим параметрам полностью соответствуют ядерным силам. Электрическая природа ядерных сил полностью укладывается в концепцию единого поля на пути к Суперобъединению взаимодействий [14].

Попытки решать подобные задачи предпринимаются давно в рамках так называемой квантовой хромодинамики (КХД), в основе которой вначале были положены три кварка, а сегодня число параметров в КХД перевалило за сотню, увеличивая количество проблем, которые необходимо решить [33]. Наряду с описанием действия ядерных сил и обоснованием заряда у адронов, а к ним относятся нуклоны, необходимо решить проблему формирования массы нуклонов, чего в принципе КХД решить не может. Это мертвая теория, которая частично реанимирована в теории УКС и ТЕЭП, если принять за кварки целые электрические и магнитные заряды (рис. 2), а взаимодействие целых кварков перенести на квантоны и оболочку нуклонов или отдельный «затравочный» заряд электрона (позитрона) [14]. В этом случае удается описывать структуру и состояние любой элементарной частицы, не только адронов, но также и лептонов, к которым относится электрон и фотон. Оказывается, достаточно всего четырех монополей (двух электрических и двух магнитных зарядов), чтобы описать не только все элементарные частицы, как открытые, так еще и неоткрытые, но и все фундаментальные взаимодействия.

Попытки объяснить наличие массы у элементарных частиц введение в квантовую теорию обменных частиц, так называемых частиц Хиггса, которые дают массу другим частицам [34,35], оказались несостоятельными, несмотря на использование сложнейшего математического аппарата. Частицы Хиггса по предсказаниям теории должны били быть обнаружены экспериментально на гигантском ускорителе (суперколлайдере) в ЦЕРНе (Женева). Но эти частицы обнаружены не были, и очень дорогой суперколлайдер пришлось закрыть за ненадобностью. Теория УКС и ТЕЭП уже сэкономила мировому научному сообществу миллиарды долларов, раскрыв структуру элементарных частиц и природу их гравитационного поля и массы [12,14].

Не удалось экспериментально обнаружить кварки, пусть косвенно в виде кварк­глюонной плазмы, которая должна наблюдаться при достижении протоном очень больших энергий порядка 200 ГэВ/нуклон [33]. КХД предсказывала, что в этом случае протон должен «расплавиться», выделив кварк-глюонную плазму. В последнее время прошли сообщения, что, какая-то плазма получена на больших скоростях и энергиях, и ее связывают с кварк­глюонной плазмой. Но у меня вызывает большие сомнения сама кварк-глюонная плазма, за которую могут принять электрон-позитронную плазму при распаде знакопеременной оболочки нуклона, если такое возможно [13]. С другой стороны, анализ эффекта Ушеренко [13] по сверхглубокому проникновению частиц микронных размеров в стальные мишени с выделением колоссальной энергии в 10 ...10 раз превосходящей кинетическую энергию частиц, позволяют судить о том, что электрон-позитронная плазма в газе обнаружена экспериментально, а также она может составлять основу шаровой молнии [6].

Теперь перейдем к самой теме данного раздела, то есть к физике открытых квантомеханических систем. Для этого необходимо понять, как формируются в квантованном пространстве-времени элементарные частицы. Двухроторная структура фотона уже была приведена на рис. 6 как специфическая частица-волна в светоносной среде, как некий квантовый сгусток энергии электромагнитной поляризации квантованного пространства-времени. То, что фотон может существовать только на скорости света, доказывает его исключительно волновую природу в светоносной среде. Фотон - это открытая система, являющаяся частью светоносной среды, без которой фотон не может образоваться и переноситься. К открытым квантомеханическим системам относятся все известные элементарные частицы, отличающиеся от фотона тем, что, фотон является единственной частице, не включающей в себя отдельных от квантона электрических зарядов монопольного типа, а только представляет собой волновое возбужденное состояние квантонов, через которые он переносится по типу одиночной волны (солитона).

Все остальные элементарные частицы включают в свой состав электрические заряды монопольного типа. Естественно, что охватить весь спектр элементарных частиц не представляется возможным. Поэтому в данной работе анализ ограничен исследованием формирования массы у нуклонов (протона и нейтрона), которые представляют собой яркий пример открытой квантомеханической системы. Наличие у нуклона знакопеременной оболочки позволяет выделить четкую гравитационную границу, способную к сферическому сжатию и растяжению, формируя гравитационное поле нуклона. Это позволяет перенести теорию гравитации нуклонов на все сферические тела, включая космологические объекты, для которых их поверхность представляет условную гравитационную границы в среде, характеризуясь среднестатистическими параметрами среды. Для тел несферической формы искажено только ближнее поле, а дальнее поле переходит в поле сферическое, подчиняясь принципу суперпозиции полей, когда сумма сферических гравитационных полей всех элементарных частиц, входящих в состав тела, определяет его гравитационное поле. У электрона и позитрона отсутствует ярко выраженная гравитационная граница, выделяя их в отдельный класс частиц с центральным затравочным зарядом, который формирует более сложное гравитационное поле [10-17].

На рис. 10 в сечении показана область квантованного пространства-времени, внутри которой сформировалась сферическая знакопеременная оболочка нуклона (пунктирная сфера) и начала сжиматься до сферы радиусом RS. Как уже отмечалось, невозмущенное квантованное пространство-время характеризуется квантовой плотностью среды р0 (6). Очевидно, что при сжатии оболочки нуклона вместе со средой, квантовая плотность р2 среды внутри оболочки увеличивается более ро, за счет растяжения внешней области, квантовая плотность р1 которой уменьшается. Так осуществляется сферическая деформация квантованного пространства-времени, в результате которого у нуклона появляется масса и гравитационное поле. При этом, оболочка нуклона выполняет функцию гравитационной границы в квантованной среде, разделяя среду с различной квантовой плотностью р1 и р2, внутри нуклона и вне его оболочки.

Рис. 10. Фомирование гравитационного поля и массы нуклона в результате сферической деформации квантованного пространтсва-времени оболочкой нуклона радиусом RS.

Знакопеременная оболочка нуклона обладает замечательным свойством. Она может проходить через неподвижное квантованное пространство-время, как рыболовная сеть проходит в воде. При движении знакопеременная оболочка нуклона сохраняет сферическую деформацию квантованного пространства-времени, обеспечивая волновой перенос массы нуклона и корпускулярный перенос знакопеременной оболочки. Экспериментально это подтверждается тем, что нуклоны подчиняются принципу корпускулярно-волнового дуализма, представляя собой частицу-волну как открытую квантомеханическую систему.

В представленной модели на рис. 10 пространство топологически изменено, когда его топология отлична от топологии недеформированного пространства. Геометрия такого пространства-времени может быть представлена множеством сфер Лобачевского с различной кривизной, нанизанных одна на другую, формируя топологию сферического пространства Лобачевского. Учитывая, что размеры квантона составляют порядка 10 м, а радиус RS нуклона - порядка 10_15 м, то по отношению к фундаментальной длине 10_25 м данного пространства радиус сфер Лобачевского представляет собой очень большую величину. Это соответствует постулатам геометрии Лобачевского и для математиков указанная область исследований является золотоносной жилой, поскольку имеет конкретное практическое приложение.

Ппредставленная на рис. 10 модель очень легко поддается математическому расчету, поскольку определена свойствами однородной квантованной среды, упругое состояние которой описывается уравнением Пуассона [10-17]. Неоходимо отметить, что до сих пор отсутсвует корректный аналитический вывод и решения гравитационного уравнения Пуассона. В общей теории относительности (ОТО) классическое уравнение Пуссона, заменено более сложным тензорным уравнением Эйнштейна, решения которого не приблизили физику к пониманию причин гравитации [36].

Любое «искривление» квантованного пространтсва-времени связано вс двумя типами деформации: сжатием и растяжением, сопутствующими друг дуругу в упругих средах. Причем деформация сжатия уравновешивается деформацией растяжения. При отсутствии второй сопротивляющейся деформации компоненты применительно к упругой квантованной среде, пространтсво должно быть неустойчивым, и любая гравитация должна была бы вызвать коллапс массы вещества в черную дыру или микродыру. Но экспериментально такой

неустойчивости квантованного пространства-времени не наблюдается. Оно прояляет свойства очень устойчивой и стабильной среды, которые указывают на наличие у пространтсва упругих свойств, способных сопротивляться любой деформации.

Именно модель сферической деформации квантованного пространтсва-времени, представленная на рис. 10, наглядно демонстрирует, что деформация сжатия оболочки нуклона до радиуса RS внутри оболочки, уравновешена деформацией растяжения квантованного пространтсва-времени с ее внешней стороны. Данная модель впервые позволяет получить корректные уравнения состояния нуклона в результате сферической деформации квантованного пространтсва-времени.

Решение задачи сводится к нахождению функции распределения в пространстве квантовой плотности среды: р1 - с внешней стороны гравитационной границы радиусом RS и р2 - внутри границы нуклона. Внутри области RS эта задача решается элементарно. Количество квантонов Nqo внутри области R объемом Vo до сжатия, и после сжатия Nq2 в RS остается постоянным, и определяется квантовой плотностью р0

4 3

Nqo = Nq2 =Р oVo = 3 ^о Р о (29)

При сжатии внутренний объем Vo уменьшился до VS, а соответственно увеличилась квантовая плотность р2

Выражение (31) определяет квантовую плотность р2 внутри области RS как величину, не зависящую от расстояния r внутри сжатой области.

Серьезную математическую проблему представляет определение функции распределения квантовой плотности р1 во внешней области от границы раздела RS в зависимости от расстояния r. Попытки прямого составления дифференциального уравнения на основе перераспределения квантовой плотности, и его интегрирование не дает положительных результатов. Уравнения получались расходящимися, а решения бесконечными. Этому есть физическое объяснение. При сжатии внутренней области RS, с внешней стороны происходит заполнение освободившегося объема квантонами, подтягивая их к границе раздела из окружающего квантованного пространства-времени. Поскольку пространственное поле непрерывно, то движение квантонов к границе раздела из внешнего поля распространяется на бесконечность, приводя к расходящимся уравнениям. Когда с такими проблемами сталкивается теоретическая физика, то приходится искать другие подходы к решению задач, поскольку существующий математический аппарат не позволяет решить проблему бесконечности.

В данном случае поставленная задача решается чисто алгебраическими методами, поскольку данное скалярное поле характеризуется абсолютными параметрами (ро, р1, р2) и нет необходимости работать с приращениями этих параметров. Чтобы решить поставленную задачу необходимо проанализировать еще одно состояние данного поля, когда непрерывное сжатие области RS достигает конечного предела, ограничившись радиусом Rg, и далее сжатие поля невозможно. Это состояние может определять состояние черной микродыры, характеризуя нуклон гравитационным радиусом Rg, который является чисто расчетным параметром, представляя собой гипотетическую границу раздела, на которой квантовая плотность среды р1 с внешней стороны падает до нуля, то есть р1^0 при RS^Rg. В результате функциональная зависимость p1(r) при удалении от нуклона на расстояние r представляет собой единственную кривую для конкретного радиуса Rg, обеспечивая баланс квантовой плотности среды

В (31) входит pj как мнимая величина, характеризующая дефицит квантовой плотности р1 относительно недеформированного пространства-времени с квантовой плотностью ро

РІ = Ро - Pi (32)

Функциональная зависимость pj определяет кривизну искривленного пространства - времени и представляет собой типичную обратную зависимость, установление которой необходимо искать в отыскании степени n самой кривизны поля 1/r”. Пока неизвестен показатель степени n, то ли это целое число 1, 2 и т. д., то ли дробное? С математической точки зрения в этом есть определенная натяжка. С позиций физики такой прием правомерен, поскольку мы задаем кривизну скалярного поля, и проверяем, насколько заданная кривизна соответствует или расходится с экспериментальными данными. Более рационально вместо кривизны 1/rn использовать ее эквивалент Rg /rn привязанный к Rg. Далее представим зависимость pj как функцию расстояния r для Rg/rn

, Rg

Р1=Р о-n-

r

Функция (34) в предельном случае при r=Rg равна нулю

Условие (35) однозначно выполняется при равенстве

Rg

= 1

Равенство (36) справедливо при n=1, что и требовалось доказать. Это возможно только в том случае, если внутри квантованного пространства-времени в любой ситуации оболочка нуклона остается сферической, определяя принцип сферической инвариантности [11].

Таким образом, искомое распределение квантовой плотности р1 (r) на любом расстоянии r определяется показателем первой степени n=1 от расстояния r

В выражение (37) входит относительная безразмерная кривизна kR пространства - времени, которая очень удобна при анализе его деформации

Rg

(38)

r

В предельном случае при r=Rg относительная кривизна поля имеет максимальную величину равную 1. Во все остальных случаях кривизна поля при удалении от области Rg уменьшается и всегда будет меньше единицы.

Если сравнивать выражения (37) и (30) распределения квантовой плотности р1 и р2, то необходимо параметры поля в (30) привести к одинаковому виду (37), выразив р2 через относительную кривизну поля kR (38). Для этого определим скачки Др1 и Др2 квантовой плотности среды на границе раздела RS относительно р0, соответственно, с внешней Др1 и внутренней Др2 сторон. Очевидно, что в силу симметрии поля на границе раздела,
увеличение квантовой плотности среды Др2 внутри, возможно за такого же уменьшения квантовой плотности Дрі с внешней стороны, обеспечивая баланс квантовой плотности на границе раздела

Арі = Ар 2

Скачек квантовой плотности среды Др1 с внешней стороны находим из (37) при условии, что r=RS

С учетом (40) и (39) находим значение квантовой плотности среды р2 внутри нуклона

( Rg 1

Р 2 =Р о +АРі =Ро 1 + ~ (41)

V RS

В результате преобразований квантовые плотности р1 (37) и р2 (41) сферически деформированного квантованного пространства-времени приведены к одинаковому виду и представляют собой систему

f Rg ї

Р1 = Ро 1--------- при r ^ RS

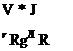r

(42) р 2 = р о

S J

где 1r - единичный вектор в направлении радиуса г.

Как видно из (43) исходное поле распределенной квантовой плотности при выполнении операции градиента переходит в векторное поле семейства векторов D, направленных из центра деформации.

Далее определяем поток ФD вектора деформации D пронизывающий любую замкнутую сферическую поверхность S вокруг границы раздела RS (центра деформации) деформированного квантованного пространства-времени

ФD = |DdS = Ро, g 4nr2 = 4проRg (44)

s r

Дивергенция определяется пределом потока поля, выходящего из некого объема к величине этого объема при его стремлении к нулю. Однако в данном случае, объем сферически деформированного пространства-времени стремится не к нулю, а предельному объему VS, определяемому радиусом RS. Это объем элементарной частицы, который очень мал, по сравнению с размерами в макромире. Приняв VS за объем близкий к нулевому, запишем гравитационное уравнение Пуассона для квантовой плотности среды

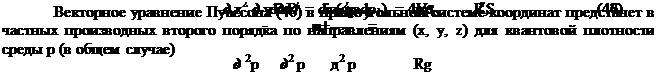или

Если проинтегрировать уравнения (46) и (47), то получим корректное решение (42) для внешней и внутренней областей относительно гравитационной границы раздела. Данная методика позволила вначале получить решение (42), а затем перейти от решения к составлению уравнения Пуассона.

Необходимо также обратить внимания, что уравнение Пуассона для квантовой плотности среды по форме записи эквивалентно уравнению Пуассона для гравитационных потенциалов. Теория тяготения, как частный случай общей теории гравитации, оперирует только одним гравитационным потенциалом, так называемым ньютоновским потенциалом фп для элементарной частицы массой m

Gm

Ф n =------- (48)

r

где G = 6,67 '10_11 Нм2/кг2 - гравитационная постоянная.

При наличии возмущающей массы М с потенциалом фп, на пробную массу m действует ньютоновская сила Fn притяжения

Fn = m ■ grad(^ n) = GmJ^ 1r

r

В общем случае поле гравитационного потенциала ф описывается уравнением Пуассона

квантовой плотности среды и поля гравитационных потенциалов, показывает, что для полного описания деформированного квантованного пространства-времени с помощью гравитационных потенциалов не хватает целого набора гравитационных потенциалов. Несомненно, что нехватка гравитационных потенциалов порождает трудности классической теории гравитации, и известное решение (48) годится только для описания нестабильного пространства, поскольку отсутствует вторая компенсирующая компонента, как в решении (42).

Чтобы обеспечить условия стабильности и устойчивости квантованного пространства - времени необходимо четырем параметрам квантовой плотности среды р0, pi, р^, р2 найти эквивалентные параметры гравитационных потенциалов. В целом, невозмущенное гравитацией квантованное пространство-время описывается квантовой плотностью среды ро (6). Необходимо найти эквивалентный гравитационный потенциал фо, который точно также, как и ро, характеризовал бы в целом невозмущенное гравитацией квантованное пространство-время. С этой целью воспользуемся принципом эквивалентности массы покоя то и ее энергии W0

W0 = moC0 (51)

Масса покоя то и ее энергии W0 связанны с гравитационным потенциалом фо. Чтобы записать эту связь необходимо расширить признаки гравитационного потенциала, который связывает не только тяготеющие массы (49), но и связывает отдельную массу, как изменение энергии W сферической деформации при рождении массы элементарной частицы, которое описывается дифференциальным уравнением

dW , ч

m = -— (52)

d9

Ранее физика рассматривала массу как меру инертности, не зная причин этой меры. Дифференциальное уравнение (52) показывает, что масса характеризуется изменением энергии W квантованного пространства-времени в результате его сферической деформации, рассматривая массу как открытую квантомеханическую систему. Это возможно только в условиях энергоемкого квантованного пространства-времени с колоссальной концентрацией энергии (7) в единице объема. В этом случае гравитационный потенциал связывает энергию и массу через соответствующие изменения энергии и потенциала

Из (53) и (51) получаем

Wo = mo ф 0 = moC2 (54)

Из (54) находим гравитационный потенциал фо квантованного пространства-времени

ф о = С (55)

В классической теории тяготения потенциал фо рассматривается как ньютоновский потенциал (48) в бесконечности. Естественно, что при такой трактовке потенциал фо принимался за нулевой. Применительно к энергоемкому квантованному пространству - времени потенциал ф0 = С0 характеризует невозмущенный гравитацией вакуум. Это фундаментальная поправка в теорию гравитации.

Из (55) следует, что квантовой плотности ро (6), невозмущенного гравитацией

вакуума, соответствует гравитационный потенциал С2. Это дополнение в теорию гравитации показывает, что рассматриваемое поле квантованного пространства-времени гравитационно в своей основе, и даже в отсутствии возмущающей массы обладает

гравитационным потенциалом С2. Гравитационный потенциал С2 - это реальный

потенциал, существующий в природе. Его доказательством служит эквивалентность массы
m0 и энергии W0 покоя. Действительно, интегрируя (52) определяем работу, связанную с переносом массы то, как гравитационного заряда, из виртуальной бесконечности с нулевым

гравитационным потенциалом, в область поля с гравитационным потенциалом С о при рождение в квантованном пространстве-времени частицы с массой то, в данном случае нуклона

с2

Wo =j mod9 = moC2 (56)

0

Выражение (56) является самым простым и понятным выводом эквивалентности массы и энергии. Обратным действием из (56) приходим к выводу, что космический вакуум

обладает потенциалом С о2 . В этом не приходится сомневаться, поскольку эквивалентность между массой и энергией - многократно проверенный экспериментальный факт. В теории УКС выражение С2 представляет собой не квадрат скорости света, а гравитационный

потенциал невозмущенного физического вакуума с размерностью [Дж/кг=м2/с2].

Но почему физика ранее не могла обнаружить наличие у вакуума гравитационного

потенциала С2, учитывая его очень большую величину? Дело в том, что потенциал С2 распределен по всему пространству, а мы можем проводить только относительные измерения, связанные с изменением гравитационного потенциала. Прямая аналогия с электрическим потенциалом, приложенным к очень большому металлическому листу, на поверхности которого стоит человек с вольтметром и не в состоянии замерить электрический потенциал листа, поскольку вольтметр измеряет только разность потенциалов.

Получить корректное решение уравнения Пуассона (50) прямым интегрированием для двухкомпонентной системы по аналогии с решением (42) еще никому не удалось. Поэтому воспользуется эквивалентностью между квантовой плотностью среды ро и гравитационным 22

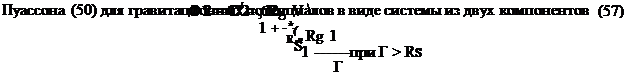
потенциалом Со. После замены р0 на Со в (42) получаем корректное решение уравнения

где ф1 и ф2 - функции распределения гравитационного потенциала для сферически

деформированного пространства-времени, Дж/кг.

Потенциал ф1 определен для внешней области за границей раздела среды Rs. Потенциал ф2 определен для области внутри сферической границы раздела Rs. В дальнейших расчетах потенциал ф1 запишем как С2. Это очень удобно, поскольку корень квадратный из ф1 определяет скорость света С в возмущенном гравитацией квантованном пространстве - времени.

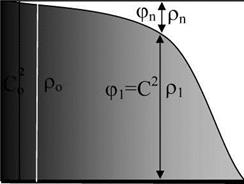
На рис. 11 представлена гравитационная диаграмма распределения квантовой плотности среды (42) и гравитационных потенциалов (57) как двухмерное представление сферически деформированного пространства Лобачевского (рис. 10). Особенностью

гравитационной диаграммы нуклона является наличие гравитационной ямы во внешней области квантованной среды за границей раздела радиусом Rs, а на границе раздела наблюдается скачок квантовой плотности среды и гравитационного потенциала. На гравитационной диаграмме наглядно можно увидеть «кривизну» квантованного пространства-времени, которая не видна на сферах пространства Лобачевского (рис. 10) в трехмерном представлении. Для сферической деформации кривизна (38) пространства
обратно пропорциональна расстоянию г до центра нуклона и зависит от величины возмущающей массы m, то есть от величины деформации (43) квантованного пространства - времени.

На гравитационной диаграмме рис. 11 четко определено место ньютоновского потенциала фп (48), как потенциала мнимого (не существующего в реальности), входящего в баланс гравитационных потенциалов

С2 = С2 -Фп (58)

Рис. 11. Двухмерное представление пространства Лобачевского в виде гравитационной
диаграммы распределения квантовой плотности среды (р1; р2) и гравитационных
потенциалов (фі, ф2) нуклона. р2 - область сжатия среды, pi - область растяжения среды.

В реальности существует только гравитационный потенциал С2, названный

потенциалов действия. Из решения (57) выпишем функцию распределения потенциала

2

действия С во внешней области от границы раздела Rs

г

Как видно, выражения (58) и (59) полностью идентичны, и при совместном их решении находим значение ньютоновского потенциала фп, через потенциал С0

2 Rg

Ф п = Со-----

Из (61) определяем значение параметра Rg

Rg = G^

сО

Выражение (62) устанавливает значение гравитационного радиуса Rg в теории УКС, которое отличается от шварцшильдовского радиуса отсутствием множителя 0 [37]. Необходимо сразу обратить внимание, что гравитационный радиус Rg (62) не применим для элементарных частиц, поскольку элементарная частица не способна к гравитационному
коллапсу. Гравитационный радиус Rg (62) в теории гравитации элементарных частиц - это чисто расчетный гипотетический параметр. В общей теории гравитации гравитационный радиус вполне реальный параметр, характеризующий предельное гравитационное сжатие (коллапс) вещества объекта в черную дыру.

Подставляя значение гравитационного радиуса Rg (62) в (46) и (47) приводим уравнение Пуассона к классическому виду (50):

Р o

Учитывая фундаментальность принципа суперпозиции полей, полученные выше формулы для поля гравитации нуклона справедливы для описания гравитационных полей любых тел сферической формы, включая космологические объекты. В этом случае, каждая элементарная частица, входящая в состав тела, концентрирует внутри себя сжатую область за счет разряжения внешней области. В результате поверхность тела можно рассматривать как гравитационную границу с радиусом RS, внутри которой среднее значение квантовой плотности и потенциала определяется параметрами р2 (42) и ф2 (47). С внешней стороны от гравитационной границы гравитационного поле тела описывается квантовой плотностью среды р1 (42) и гравитационным потенциалом действия С (47). В случае, когда тело сжимается в черную дыру (микродыру), радиус RS уменьшается до гравитационного радиуса

Rg (62).

2Co

А

Р2

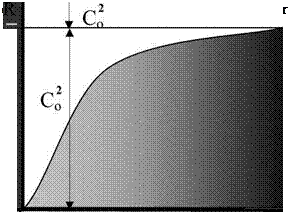
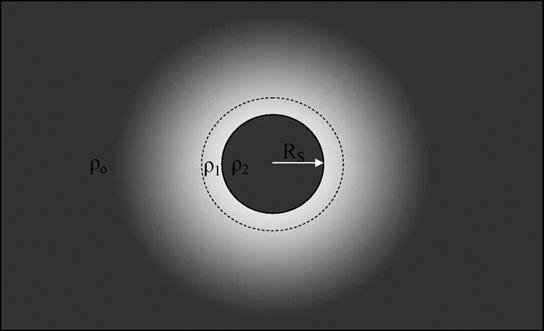
Рис. 12. Гравитационная диаграмма черной дыры (микродыры) при сжатии
гравитационного радиуса RS (рис. 11) до гравитационного радиуса Rg.

На рис. 12 представлена гравитационная диаграмма черной дыры (микродыры) в результате сжатия вещества тела с радиусом RS (рис. 11) до гравитационного радиуса Rg (62). Отличительным свойством черной дыры является наличие разрывов квантованного пространства-времени как светоносной среды на ее поверхности с радиусом Rg. Подставляя r= Rg (62) в (42) и (57) находим, что на поверхности черной дыры с внешней стороны квантовая плотность рі=0 и гравитационный потенциал действия С2=0. Наличие разрывов светоносной среды на поверхности черной дыры определяет условия, когда свет не может
проникнуть во внутрь черной дыры, и выити из нее наружу, делая черную дыру невидимой. Это подтверждается расчетами, полагая, что потенциал действия С2 (57) определяет скорость

света в квантованной среде из баланса гравитационных потенциалов

Подставляя значение ньютоновского потенциала (60) фп= Со на поверхности черной

дыры в (65) определяем, что свет на ее поверхности останавливается С=0. Регистрация объектов типа черной дыры экспериментально доказывает, что ее невидимость определяется разрывами светоносной среды. С другой стороны, выражение (65) позволяет определять скорость света С в возмущенном гравитацией квантованном пространстве-времени.

Таким образом, для описания области сферически деформированного пространства - времени теория УКС и ТЕЭП использует четыре гравитационных потенциала: Co, С, фп, ф2 (57) в отличие от классической гравитации, которой известен только один ньютоновский потенциал фп тяготения. Незнание дополнительных трех гравитационных потенциалов Co,

С2, ф2 делает все попытки физиков-теоретиков малоэффективными в продвижении теории гравитации. Учитывая, что каждому значению гравитационного потенциала соответствует своя квантовая плотность среды (42), запишем соотношения между ними через коэффициент кф, обозначив р^ (32) как рп, то есть р^ = рп, соответствующие ньютоновскому потенциалу фп (60)

і ро р1 рп р2 л і л58 квантонов кг

Ф c2 C2 фп ф2 Дж м3

Замена ньютоновского потенциала фп (60) потенциалом действия С2 (64) в законе всемирного тяготения Ньютона также не меняет силы притяжения Fn (49)

2 2 mM

Fn = m - gradС2 = m - grad(С2 - фn) = G—— 1r (67)

r2

Таким образом, замещение ньютоновского потенциала фп потенциалом действия С2, в том числе в уравнении Пуассона в теории УКС и ТЕЭП не меняет известных положений теории тяготения, и значительно расширяет возможности теории гравитации. Но главное, дает физическое понимание процессов происходящих в вакууме при его гравитационном возмущении, определяя основы квантовой теории гравитации (КТГ) в результате сферической деформации квантованного пространства-времени, когда носителем

гравитационного поля выступает квантон.