Количество тепла Q измеряется в калориях.

Удельной весовой теплоемкостью с называют количество тепла, необходимое для нагрева 1 г данного вещества на 1 °С. Удельная теплоемкость с измеряется в кал 1(г ■ °С).

Удельной объемной теплоемкостью называют количество тепла, необходимое для нагрева 1 см3 данного вещества на I °С. Объемная теплоемкость измеряется в кал!(см6 • °С).

Из определения очевидно, что объемная теплоемкость равна весовой теплоемкости, умноженной на плотность данного ве­щества - су.

В разных условиях теплоемкость тела различна. Для твердых тел она может существенно изменяться в зависимости от темпера­туры, а для газов, кроме того, еще и от давления. Таким образом, для нагрева данного тела на 1 °С в каждом новом интервале темпе­ратур будет затрачиваться различное количество тепла.

Если, вводя некоторое количество тепла Q, кал, нагреть тело, имеющее вес G, от температуры Т, °С до Т2 °С, то можно опреде­лить среднее значение теплоемкости вещества для данного интер­вала температур:

с — щ^~ту) кал^г • °Q - (IV. 1)

Истинная теплоемкость с при температуре Т

ст = кал/(г - °С). (IV.2)

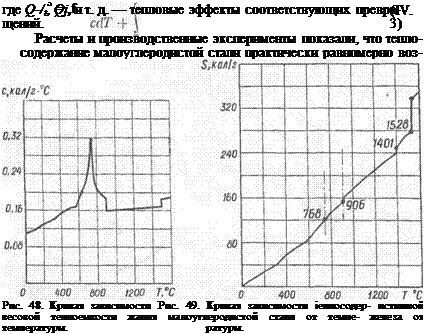
Как видно из рис. 48, истинная весовая теплоемкость же­леза в интервале температур 0—1600 °С изменяется довольно сильно. Пик этой кривой 132 кал/(г • °С)| соответствует критической точке магнитного превращения (точке Кюри) — 768 °С.

При температуре плавления (для железа, например, при 1535 °С) сообщаемое телу тепло идет не на повышение температуры, а на рас­плавление металла, поэтому здесь понятие истинной теплоемкости не имеет смысла. Сказанное относится и к критическим температу­рам перехода железа из одной модификации в другую (a - Fe-> y-Fe при911 °С и y-Fe -»• б-Fe при 1392 °С), а также к точке маг­нитных превращений.

Количество тепла, необходимое для того, чтобы нагреть 1 а ве­щества от 0 °С до заданной температуры, называется теплосодержа­нием S, каліг. Для вычисления теплосодержания нужно проинтегри­ровать произведения rdT истинной весовой теплоемкости на беско­нечно малые приращения температуры в интервалах, где теплоем­кость не имеет скачков, и учесть тепловые эффекты превращений

в критических точках. Тогда общее выражение для теплосодержа­ния тела будет иметь вид

растает до температуры плавления, при которой наблюдается рез­кий скачок, связанный с затратами тепла на превращение стали из твердого состояния в жидкое (рис. 49). Такой характер измене­ния теплосодержания позволяет для упрощения расчетов не учи­тывать тепловые эффекты превращений в стали в интервале 0— 1500 °С и пользоваться средним значением теплоемкости

с = 2ш> = Jgi = 0,173 калКг - °С).

Распределение температур по поверхности и объему тела ха­рактеризуется температурным полем, которое представляет собой совокупносгь температур всех точек тела в данный момент времени. Его можно изобразить графически или при помощи математических выражений,

Если нагреть тонкий лист металла неподвижным пламенем аце­тилено-кислородной горелки или электрической дугой, а затем за­мерить температуры поверхности листа на разных расстояниях

от источника тепла, например в точках 1 и 2 (рис. 50), и отложить в масштабе над каждой точкой листа отвечающую ей температуру Ту и Т2, то концы ординат образуют поверхность вращения, изобра­жающую температурное поле. В рассмотренном примере ряд точек поверхности имеет одинаковую температуру. Соединив на чертеже точки с одинаковой температурой, получим линии равных темпе­ратур, или изотермы, по характеру которых также можно судить о температурном поле.

Изотермы для случая нагрева неподвижным источником тепла показаны на рис. 51. Поскольку практически свойства стали одина­ковы по всем направлениям и тепло распространяется го все сто­роны с равной интенсивностью, изо-

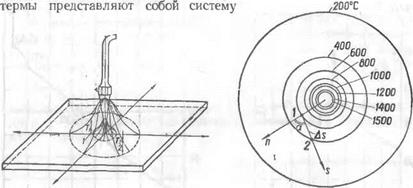Рис. 50. Характер температурного по - Рис. 51. Изотермы температур-

ля при нагреве листа неподвижной аце - ного поля при иагреве пластины

тилено-кислородной горелкой. из малоуглеродистой стали не­

подвижным источником тепла (мощность источника q — концентрических окружностей. При = 750 кал/сек). небольшой толщине листа прогрев

его по толщине можно считать равномерным. В этом случае, точки с одинаковой температурой располагаются на цилиндри­ческой поверхности, которая представляет собой изотермическую поверхность. В общем случае изотермической поверхностью назы­вается геометрическое место точек тела, имеющих одинаковую тем­пературу. При перемещении источника тепла, а также неравномер­ном распределении температур по толщине изделия, изотермы при­обретают гораздо более сложный вид.

Если в процессе сварки быстро перевернуть пластину и вылить из сварочной ванны жидкий металл и шлак, то в пластине образу­ется углубление, которое может служить наглядным примером изо­термической поверхности при сварке. Все точки этой поверхности в момент опрокидывания имели одинаковую температуру плавле­ния стали.

Чтобы получить математическое выражение для температурного поля, нужно написать уравнение, снизывающее температуры с ко­
ординатами точек тела х, у, г, а для поля, меняющегося во времени,— еще и со временем /. Следовательно, в общем виде такие зависимости будут выражены как Т (ж, у, г, /).

При перемещении в температурном поле от одной точки к другой по направлению, не совпадающему с изотермой, температура не­прерывно меняется. Скорость изменения температуры при переме­щении по заданному направлению может быть различной. Она за­висит от характера температурного поля и от направления, по кото­рому совершается перемещение. Выберем на заданном направлении* точки / и 2, отстоящие друг от друга на As (рис. 51). Если в точ­ках 1 и 2 температуры соответственно равны Тх и Т2, то скорость изменения температуры по заданному направлению на пути As можно оценить величиной изменения температуры в градусах Цельсия,

приходящейся на единицу длины, т. е. —!. Полученная скорость

будет средней для данного интервала и может значительно отлича­ться от истинных скоростей изменения температуры в точках 1 и 2. Приближая точку 2 к точке 1 до бесконечно малого значения As, уменьшаем тем самым разность Тг—Тг и в пределе получим истин­ное значение скорости изменения температуры в точке 1 по задан­ному направлению:

Т2 - 7 , і =дТ As l&s-*o ds '

Эта характеристика температурного поля носит название градиента температур в данной точке поля по направлению s.

Величина градиента температур в направлении, совпадающем с касательной к изотерме, будет равна нулю, так как точки тела, расположенные на изотерме, имеют одинаковую темпера­туру и (Тг—Тi) = 0. Максимальное значение градиента темпера­тур наблюдается всегда в направлении, совпадающем с нормалью к изотермической поверхности в данной точке. Такой градиент температур называется нормальным. Градиент температур по за­данному направлению s

дТ дТ п, дп

з - — a - cos а, так как os —--------- .

OS дп COS a

Таким образом, градиент температур — это векторная величина. Положительное значение он приобретает в том случае, если Т1<7’2, т. е. в направлении возрастания температуры. При 7 > Тг гра­диент имеет отрицательное значение.