ОСНОВНЫЕ ПОЛОЖЕНИЯ ДИСЛОКАЦИОННОЙ ТЕОРИИ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ МЕТАЛЛОВ
 18 апреля, 2016
18 апреля, 2016  Oleg Maloletnikov
Oleg Maloletnikov 
 Реальные критические напряжения, вызывающие появление пластической деформации, на несколько порядков ниже теоретических. Такое несоответствие привело к мысли о том, что сдвиг атомов происходит не одновременно по всей плоскости скольжения, а последовательно распространяясь от места нарушения структуры в глубь металла. Этот процесс, как и многие другие, хорошо объясняется с точки зрения теории 'Т несовершенств металла, или
Реальные критические напряжения, вызывающие появление пластической деформации, на несколько порядков ниже теоретических. Такое несоответствие привело к мысли о том, что сдвиг атомов происходит не одновременно по всей плоскости скольжения, а последовательно распространяясь от места нарушения структуры в глубь металла. Этот процесс, как и многие другие, хорошо объясняется с точки зрения теории 'Т несовершенств металла, или
теории дислокаций.
Рассмотрим подробнее наиболее важные виды дислокаций и их свойства.
Виды дислокаций. В металлических кристаллах на-
|
Вектор сдвига
Рис. 14. Схема построения вектора Бюргерса для линейной дислокации. |
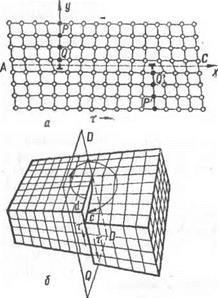
иболее часто встречаются линейные и винтовые дислокации (рис. 13).
Можно представить себе, что линейные дислокации возникают в результате введения в идеальную кристаллическую решетку добавочных атомных плоскостей Р—Q и Р'—Q', перпендикулярных к плоскости чертежа (рис. 13, а). Если добавочная атомная плоскость {экстраплоскость) введена над плоскостью скольжения А—С, то образующаяся в таком случае линейная дислокация Считается положительной и обозначается _1_. Введение экстраплоскости под плоскостью скольжения дает отрицательную линейную дислокацию, обозначаемую знаком Т.
Знак дислокации имеет существенное значение. Если, например, две дислокации разных знаков, изображенные на рис. 13, а, совместить таким образом, чтобы их экстраплоскости совпали, то,
очевидно, они взаимно уничтожатся. Совмещение же однозначных дислокаций не приведет к их исчезновению. Линейная дислокация не обязательно должна быть прямой, чаще она представляет собой замкнутую петлю, спираль и т. п.
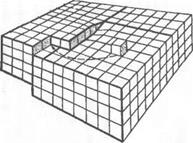
 Строение винтовой дислокации можно представить следующей схемой. Если мысленно надрезать кристалл плоскостью Q и сдвинуть надрезанные концы на одно межатомное расстояние (рис. 13, б), то расположенные горизонтально атомные плоскости изогнутся и создадут винтовую поверхность вокруг линии D—D. Следуя в направлении стрелки отточки d по первой атомной плоскости, мы придем в точку с на второй атомной плоскости и так далее по винтовой линии до нижней поверхности кристалла.
Строение винтовой дислокации можно представить следующей схемой. Если мысленно надрезать кристалл плоскостью Q и сдвинуть надрезанные концы на одно межатомное расстояние (рис. 13, б), то расположенные горизонтально атомные плоскости изогнутся и создадут винтовую поверхность вокруг линии D—D. Следуя в направлении стрелки отточки d по первой атомной плоскости, мы придем в точку с на второй атомной плоскости и так далее по винтовой линии до нижней поверхности кристалла.
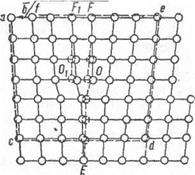
Для характеристики дислокации введено понятие вектора сдвига (вектор Бюргерса), с помощью которого оценивают вели чину искажения решетки, а следовательно, и энергию искажения.
Чтобы пояснить это, построим контур линейной дислокации, отсчитывая от точки а одинаковое количество атомов последовательно вниз, вправо, вверх и влево (рис.
14). Получим незамкнутый контур acdef. Для замыкания контура нужно от точки f провести вектор_ в точку а — это и будет вектор сдвига. Обычно его обозначают Ь. Аналогичным путем можно построить вектор Бюргерса и для винтовой дислокации.
С помощью вектора сдвига можно определить силы, необходимые для перемещения дислокации, энергию ее и т. п. Вектор Бюргерса обладает некоторыми особенностями, знание которых позволяет производить с ним математические операции. К числу наиболее важных особенностей относятся следующие:
1) величина вектора Бюргерса вдоль линии дислокации остается постоянной;
2) вектор Бюргерса всегда направлен по нормали к линейной дислокации и параллелен винтовой;
3) вектор Бюргерса для контура, охватывающего несколько дислокаций, равен геометрической сумме их векторов.
Перемещение дислокаций. При изменении напряженного состояния кристалла дислокации могут сравнительно легко перемещаться по его объему. При этом возможны два случая перемещения дислокаций: скольжение и диффузионное перемещение.
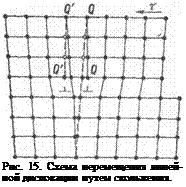
Механизм перемещения линейных дислокаций путем скольжения можно проследить на рис. 15. В начальный мдмент экстр арлоскость Q—Q испытывает усилия со стороны обеих граничащих с ней нормальных атомных плоскостей
 |
и потому' находится в равновесном состоянии. При увеличении напряжения достаточно незначительного перемещения атомов, чтобы она превратилась в обычную атомную плоскость. Теперь экстраплоскостью станет уже соседняя плоскость Q’—Q', которая также находится в равновесии, а дислокация переместится на одно межатомное расстояние. При достаточной величине напряжения этот процесс может повторяться много раз до тех пор, пока дислокация
не дойдет до поверхности кристалла, где образуется ступенька в одно межатомное расстояние (точнее, в один вектор сдвига).
Процесс движения дислокации осуществляется очень легко, так как при этом происходит не передача масс, а только незначительное перемещение одного ряда атомов. При таком, несколько упрощенном представлении о механизме движения дислокации, ее перемещение должно происходить вообще без дополнительной затраты энергии, поскольку при любом положении экстраплоскости силы, действующие на нее с одной и другой стороны, равны.
На самом деле для каждого акта перемещения дислокации нужно преодолеть определенный энергетический барьер. Поэтому для скольжения дислокации требуется некоторое минимальное напряжение тр. Величину этого напряжения приближенно определяют по формуле
2r. iu
тр = QeT кГ/мм2, (11.5)
где b — вектор Бюргерса, мм;
G — модуль сдвига, кГ/мм2;
to — ширина дислокации, мм;
е — основание натуральных логарифмов.
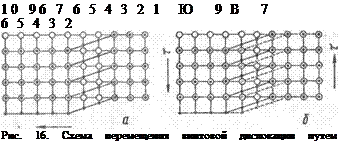
Перемещение винтовых дислокаций происходит несколько сложнее, но по тому же принципу и так же легко, как и линейных дислокаций. Схема перемещения винтовой дислокации показана на рис. 16: рис. 16, а соответствует начальному состоянию, при котором эта дислокация расположена в пределах рядов 3—6; рис. 16, б — измененному положению дислокации, сместившейся на одно межатомное расстояние влево.
Диффузионное движение дислокаций происходит сравнительно медленно, как и вообще все процессы, свя-
![]()
занные с диффузией. Так могут перемещаться только линейные дислокации. Предположим, что вследствие диффузии край экстраплоскости Q—Q (рис. 15) приобретает новые ряды атомов или, наоборот, теряет их. В первом случае дислокация будет перемещаться вниз, в глубь металла, тогда как во втором она постепенно уходит вверх и может вообще выйти на поверхность кристалла и вырваться в окружающее пространство. При комнатной температуре процессы диффузионного перемещения дислокаций протекают медленно и не имеют большого значения, но с увеличением температуры они быстро активизируются.
В реальных условиях чаще всего встречаются дислокации смешанного типа, одни участки которых являются линейными, а другие — винтовыми. Так, дислока-
|
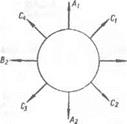
Рис. 17. Дислокационная петля. |
ционную петлю (рис. 17) можно представить как дислокацию смешанного типа. При указанном направлении вектора сдвига участок Л і является положительной, а А2 — отрицательной линейной дислокацией. Соответственно участки Вг и В„ представляют собой правую и левую винтовые дислокации. На участках СьСг, С3,С4 имеет место дислокация смешанного типа (рис. 18).
Образование дислокаций происходит: 1) в процессе первичной кристаллизации металла; 2) при срастании отдельных кристаллов; 3) путем превращения скопления вакансий в дислокацию; 4) из источников Франка — Рида.
Иногда в самом процессе первичной кристаплизации какая-либо причина заставляет атомы укладываться так, что они создают
дислокации. Если, например, представить себе кристалл в виде винтовой дислокации, то на его поверхности постоянно будет образовываться ступенька, в углу которой наиболее вероятно будет удерживаться атом (рис. 19). При достраивании в угол атом удерживают связи трех атомных плоскостей, тогда как в других случаях — только одной
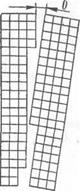
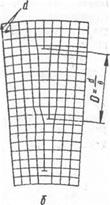 Возможны и другие схемы кристаллизации, приводящие к возникновению дислокаций. Например, при срастании зерен или блоков, расположенных под небольшим углом 6 друг к другу, на границе их, как правило, появляется цепочка линейных дислокаций (рис. 20). В этом случае расстояние D между дислокациями почти постоянно, так как зависит лишь от параметра решетки кристалла
Возможны и другие схемы кристаллизации, приводящие к возникновению дислокаций. Например, при срастании зерен или блоков, расположенных под небольшим углом 6 друг к другу, на границе их, как правило, появляется цепочка линейных дислокаций (рис. 20). В этом случае расстояние D между дислокациями почти постоянно, так как зависит лишь от параметра решетки кристалла
|
|
Рис. 19. Образование винтовой ди - Рис. 20. Образование цепочки линейных слокации при кристаллизации. дислокаций в процессе кристаллизации.
йиуглаб. Из геометрических соображений очевидно, чтоD —
или, поскольку угол 0 мал, D — ^ .
Дислокации возникают также в результате появления вакантных узлов в кристаллической решетке и объединения их в колонии. Цепочка вакансий образует своеобразную полость, которая при соответствующих условиях может сомкнуться и дать две или большее число дислокаций.
Наибольшее значение для понимания процессов пластической деформации имеет возникновение дислокаций под действие^ внешней нагрузки. При нагружении образца или изделия напряжения в нем повышаются и вызывают появление дислокаций. Механизм этого процесса, описанный Франком и Ридом, заключается в следующем. Предположим, что в плоскости чертежа расположена линейная дислокация длиной /, концы которой закреплены в точках DuD' (рис. 21, о). При увеличении напряжения дислокация D—D' начинает выгибаться. В начальный момент радиус г кривизны дис
локации велик, поэтому для дальнейшего ее изгиба требуются сравнительно малые напряжения, так как
X = ~ кг/мм2, (II.6)
где О — модуль сдвига, кГ/мм2;
b — вектор Бюргерса, мм.
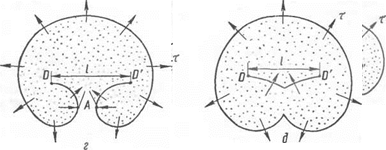 |
С увеличением напряжения радиус кривизны уменьшается до тех пор (рис. 21,6), пока дислокация не примет форму полуокруж-
Рис. 21. Образование дислокаций из источников Франка — Рида.
ности [г — ~2) • Максимальным (критическим) напряжением в этом a. G6
случае, очевидно, будет Ткр = у. из чего следует, что с увеличением размеров источника Франка — Рида критическое напряжение уменьшается, а с уменьшением — растет. Дальнейшее развитие дислокации связано с ростом радиуса кривизны (рис. 21, в) и потому может происходить без увеличения напряжения — самопроизвольно. Как только правая и левая части дислокации сомкнутся в точке А (рис. 21, г), она разделится на наружную дислокацию, которая примет форму окружности, и внутреннюю, которая возвратится в исходное положение (рис. 21, д). При достаточном напряжении этот процесс может повториться много раз. Каждая наружная дислокация, если она не встречает на своем пути препятствий, распространяется до поверхности кристалла и вызывает пластический сдвиг атомных плоскостей на один вектор Бюргерса.
В реальном металле всегда есть препятствия распространению дислокаций в виде других дислокаций, расположенных вне плоскости скольжения, или различного рода включений ит. п. Остановленные дислокации оказывают сильное влияние друг на друга, а также на источник Франка — Рида, в результате чего действие его прекращается до тех пор, пока не повысится напряжение. Большое число задержанных или вышедших на поверхность металла дислокаций образует полосу скольжения. Такие полосы можно наблюдать на поверхности пластически деформированного образца под микроскопом, а иногда и невооруженным глазом.
Препятствия движению дислокаций. В связи с тем, что в реальных кристаллах движение дислокаций затруднено различного рода препятствиями, действительное напряжение, при котором происходит перемещение дислокаций, оказывается выше теоретического и в значительной степени зависит от количества, размеров препятствий и их природы. Вследствие этого действительное напряжение, необходимое для возникновения сдвига, может изменяться в широких пределах. Наиболее существенными препятствиями становятся дислокации, расположенные в различных плоскостях скольжения, чужеродные атомы, входящие в твердый раствор, вторичные фазы, выделенные в виде самостоятельных кристаллических образований, границы зерен и др.
Увеличение числа дислокаций в объеме металла может повышать критическое напряжение сдвига и тем самым упрочнять металл. Кроме чисто силового воздействия дислокаций друг на друга, приводящего к торможению их движений, есть и другие задерживающие факторы.
Увеличение числа чужеродных атомов в металле весьма существенно затрудняет движение дислокаций и увеличивает критическое сопротивление сдвигу. Это обстоятельство является одной из причин повышения прочности металлов при их легировании элементами, образующими твердый раствор, например углеродом.
Отдельные частицы вторичной кристаллической фазы представляют собой механическое препятствие распространению дислокационных волн. Наличие в металле частиц кристаллической вторичной фазы обычно затрудняет пластический сдвиг, повышает прочность и твердость сплава.
Влияние величины зерна на характер перемещения дислокаций проявляется прежде всего в том, что крупнозернистый металл отличается большими размерами дислокаций и значительной длиной источников Франка — Рида. Эти источники начинают генерировать дислокации при меньших значениях напряжений. Кроме того, проходя через объем поликристалла, дислокации встречают меньшие сопротивления в случае более крупных кристаллов, так как границы зерен обычно содержат скопления инородных включений и дислокаций.
Некоторые способы упрочнения металла как раз и осноданы на
создании препятствий перемещению дислокаций. Одним из таких способов является упрочнение наклепом. В ходе пластической деформации создается так много дислокаций, что они мешают друг ДРУП'. повышают сопротивление сдвигу, затрудняют протекание пластической деформации. На кривой растяжения этот процесс изображается участком от — щ.
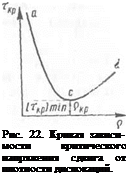 Зависимость сопротивления сдвигу (критического напряжения сдвига) от плотности р дислокаций представлена на рис. 22. При малом количестве дислокаций увеличение их числа резко снижает сопротивление сдвигу до некоторого минимального значения, соответствующего критической плотности дислокаций Ркр Пслі2 (участок ас). Дальнейшее повышение плотности отвечает упрочнению при наклепе (участок cd). Значение рКр составляет приблизительно 107—108 дислокаций на 1 см2 и относится к хорошо отожженным металлам.
Зависимость сопротивления сдвигу (критического напряжения сдвига) от плотности р дислокаций представлена на рис. 22. При малом количестве дислокаций увеличение их числа резко снижает сопротивление сдвигу до некоторого минимального значения, соответствующего критической плотности дислокаций Ркр Пслі2 (участок ас). Дальнейшее повышение плотности отвечает упрочнению при наклепе (участок cd). Значение рКр составляет приблизительно 107—108 дислокаций на 1 см2 и относится к хорошо отожженным металлам.
Из рис. 22 видно, что гораздо более эффективно упрочнение металлов за счет уменьшения числа дислокаций, однако в этом отношении сделано еще очень мало.
Существующие методы производства металлов дают количество дислокаций, большее критического, поэтому для упрочнения металлов пока - более доступен путь увеличения числа дислокаций. Уменьшение числа несовершенств в строении металла достигается при многократных его переплавах (элсктрошлаковом, электронно-лучевом, вакуумном и др.).
Общая схема процесса пластической деформации металлов. В поликристаллическом образце отдельные кристаллы ориентированы по отношению к действующему на них усилию произвольно. В то же время в каждом из них есть плоскости наиболее легкого сдвига. Поэтому в процессе нагружения перемещение дислокаций начинается неодновременно и происходит прежде всего в тех кристаллах, где направление плоскостей сдвига случайно совпадает с направлением максимального тангенциального напряжения. При этом дислокации, уже имеющиеся в этих плоскостях к моменту начала нагружения, движутся К границам кристаллов и к поверхности образца.
Вместе с тем, наиболее крупные источники Франка — Рида начинают генерировать дислокации. Это продолжается до тех пор, пока остановленные у препятствий дислокации не «закупорят» источники и не прекратят их действие. Дальнейшее повышение напряжений вновь активизирует эти источники; кроме того, дислокации начинают образовывать источники меньших размеров. Этот процесс происходит теперь не только в плоскостях, совпадающих по направлению с максимальным тангенциальным напряжением, но и в других, ориентированных более или менее благоприятно. Постепенно
(
образуется объемная сетка дислокаций, расположенных преимущественно по границам зерен и блоков. /
Повышение плотности дислокаций увеличивав/их давление на препятствия, в результате чего может произойти разрушение последних. Если этого не случится, дислокации обходят препятствие и продолжают свое движение к поверхности образца. Некоторые остановленные дислокации оказываются закрепленными по концам и превращаются в новые источники Франка f— Рида.
В процессе нагружения отдельные дислокации взаимодействуют друг с другом, взаимно уничтожаются или объединяются в колонии и группы. При достаточном напряжении группы дислокаций выходят на поверхность образца, в результате чего появляются линии скольжения. Направление этих полос определяется направлением минимальной затраты энергии и зависит как от типа кристаллографической решетки металла, так и от его поликристаллического строения.
Таким образом, пластическую деформацию поликристаллического образца или детали следует рассматривать как результат элементарных сдвигов, происходящих в отдельных кристаллах вследствие развития и перемещения дислокаций, а также других несовершенств кристаллической решетки металла.

 Опубликовано в
Опубликовано в