Распределение напряжений и деформаций в телах вращения (осесимметричных телах) представляет большой практический интерес, так как такие тела охватывают большой класс сварных конструкций (трубы, обечайки, цилиндры и т. п.; рис.7.13).

Предположим, что при сварочном нагреве возникает осесимметричное температурное поле (оно не зависит от угла 0 ). Это справедливо, если источник теплоты кольцевой с равно­мерно распределенной по окружности тепловой мощностью (например, при точечной сварке, контактной свар­ке оплавлением и диффузионной свар­ке тел вращения) или источник дви­жется по окружности с достаточно большой скоростью (например, при дуговых и лучевых способах сварки на большой скорости). Предположим также, что внешняя нагрузка и распре­деление свойств металла также осесимметричны. Тогда вслед­ствие симметрии напряженно-деформированное состояние в любом сечении по оси симметрии тела 8авиоих от координат г к к. и не зависит от координаты 0 • Таким образом, осесимметрн - ческая задача в математическом отношении является двумерной и может быть решена в строгой постановке с помощью совремеи-

пых вычислительных средств.

В осесииыетрическои случае радиальные деформации ег вы­зывают деформации в окружном направлении s. e и окружные (тангенциальные) напряжения б0 . Таким образом, из шести компонент напряжения ненулевыми являются радиальные 6r, осе­вые бг, окружные и касательные тга напряжения, а остальные касательные напряжения равны нулю, т^0=*О).

В этом состоит отличительная особенность осесимметрического случая. Деформации и напряжения схематически показаны на

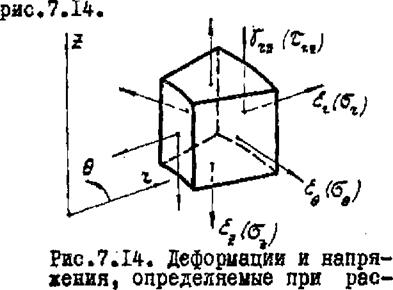Уравнение связи при­ращения деформации с на­пряжением легко полу­

чить из соответствующих уравнений для объемного напряженного и деформи­рованного состояний (7*27)-(7.32), полагая 'са. а= 0 и

Ігв - І*.я=

(7.72)

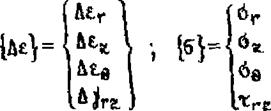
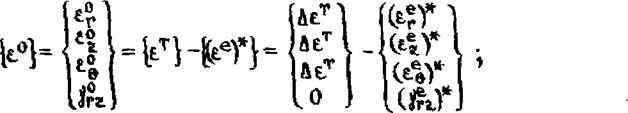Где

Решая последнее уравнение относительно напряжений, по­

лучим

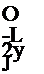где

№

При упругом деформировании материала (у = i/et ) по­следнее уравнение переходит в известное уравнение теории тер­моупругости, связывающее напряжение и деформацию за весь период нагружения:

Алгоритмы решения осесимметрической задачи и плоских задач принципиально не отличаются. Все рассмотренные в этом параграфе задачи о сложном напряженном состоянии решаются в той же последовательности, как и одномерные, которые рас­сматривались в § 7,2 (см. рис.7.8). Принципиальное отличие между одномерными и двумерными задачами состоит в решении по­следовательности линейных задач, к которой приводятся пласти­ческие задачи.