Область корректного применения критериев линейной механики раз­рушения оіраничена целым рядом условий, которые полностью выполняют­ся только при невысокой пластичности материала, значительных размерах сечения и трещиноподобного концентратора в нем и схеме нагружения тре­щины, близкой к нормальному отрыву. На практике бывают попытки при­менения этих критериев за пределами области их корректности, так как в утвержденных нормативных документах других критериев, пригодных для оценки опасности внезапного разрушения конструкций, практически не су­ществует.

Таким образом, возникают две актуальные задачи:

• оценить возможную погрешность при применении в конкретных ус­ловиях критериев ЛМР (в частности, наиболее известного из них — вязко­сти разрушения Кк) и оценить целесообразность их применения;

• предложить методику их определения и применения, сводящую по­грешности к минимуму.

С позиций теории ЛМР погрешности связаны с тем, что критерии ЛМР не полностью учитывают особенности распределения НДС у концен­тратора. Это распределение в функции расстояния от вершины концентра­тора может быть представлено в виде степенного ряда, причем критерии ЛМР учитывают только один, хотя и наиболее существенный, из членов ря­да. Погрешности от неучета других членов ряда возрастают по мере умень­шения размеров сечения, притупления концентратора, роста пластической зоны и т. д., и их можно вычислить. Недостатком такого аналитического подхода к оценке точности является сложность приемов решения, нарас­тающая по мере усложнения конструкции, и неизбежность упрощений и до­пущений, ставящих под сомнение полученный результат.

Еще одна погрешность, характерная для вязких материалов, связана с тем, что нестабильному разрушению, для описания которого предназначена ЛМР, может предшествовать устойчивый рост трещины от исходного де­фекта. В этом случае использование в расчете начального размера дефекта вносит искажение в определяемое значение критерия ЛМР.

При наличии необходимых исходных данных о геометрии конструк­ции и концентратора, а также деформационных характеристик материалов, из которых она изготовлена, МКЭ позволяет определить НДС с достаточной степенью точности. Рассмотрев полученное распределение НДС у вершины концентратора, можно сопоставить его с тем, которое дает аналитический расчет по ЛМР. МКЭ позволяет также моделировать рост трещины в про­цессе нагружения.

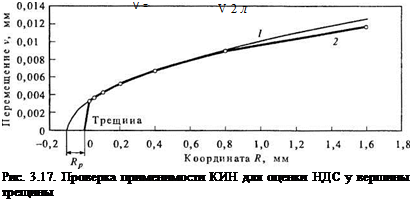
Рассмотрим вначале состояние у вершины исходной трещины в упру­гопластическом материале (сталь 15Х2МФА) до момента ее страгивания. Решение задачи проведено с помощью программного комплекса «СВАРКА». Сопоставление решения с ЛМР можно проводить как по распределению од­ного из компонентов напряжения на продолжении трещины, так и по рас­пределению раскрытия ее берегов. Результаты такого сопоставления пока­заны на рис. 3.17.

На рисунке видно, что профиль раскрытия берегов трещины v по МКЭ (кривая 2) существенно отличается от квадратичной параболы, получаемой согласно ЛМР. Однако если ввести поправку Ирвина на размер пластиче-

ской зоны, т. е. считать расчетную трещину несколько длиннее реальной, то можно добиться близкого соответствия решения по ЛМР (кривая /)

с полученным решением МКЭ в некоторой зоне у вершины трещины (кри­вая 2). Отклонение от ЛМР увеличивается как при приближении к вершине трещины (вследствие пластических деформаций), так и при удалении от нее (например, вследствие близости свободной поверхности детали). В формуле

(3.9) G — модуль сдвига, р — коэффициент Пуассона, R — расстояние точ­ки поверхности исходной трещины от ее вершины. Совмещение кривых 1 и 2 в интервале значений R от 0,1 до 0,5 мм позволяет определить из (3.9) К[ и Rp. На рис. 3.17 видно, что для данного случая близкое соответствие кривых достигается при поправке Ирвина Rp= 0,1 мм.

Найденные значения Kj и Rp можно применить для К-тарировки, т. е. найти поправочный коэффициент Y в формуле

К і = Y<j^jn(l + Rp) (3.10)

и использовать эту формулу для расчета К в данном концентраторе при других номинальных напряжениях а в сечении и других размерах трещины /, считая Y и Rp постоянными.

Если известно, хотя бы ориентировочно, значение вязкости разруше­ния К1с для данной марки стали, то, проведя моделирование МКЭ для уровня нагрузки, соответствующего этому значению К, у концентратора, можно в первом приближении оценить корректность использования ЛМР в расчете на прочность и необходимость соответствующих испытаний материала. Зо-

на разрушения контролируется критериями ЛМР, если область совпадения результатов расчета по ЛМР с результатами решения МКЭ (см. рис. 3.17) достаточно широка и начинается достаточно близко от вершины трещины. Обычно «достаточно близким» считают расстояние, меньшее размера структурного элемента, который превышает на порядок размер зерна поли­кристалла и составляет для конструкционных сплавов от десятых до сотых долей миллиметра.

В качестве критерия механики разрушения можно принять перемеще­ние на контуре радиусом 0,5 мм, окружающем вершину трещины. По дру­гим данным, этот радиус для конструкционных сталей должен составлять 0,23 мм. Таким образом, в рассмотренном примере найденные значения К и Rp обеспечивают необходимое соответствие моделей, что свидетельствует о применимости критерия ЛМР для сопоставления вариантов конструктивно­технологических решений.

Более обоснованный вывод о применимости механики разрушения к расчету конструкции можно сделать на основе анализа процесса ее разру­шения. Расчет по критериям механики разрушения необходим, если в про­цессе роста трещины возможен переход к нестабильному разрушению, т. е. к росту трещины при постоянной или снижающейся внешней нагрузке за счет накопленной в конструкции потенциальной энергии.

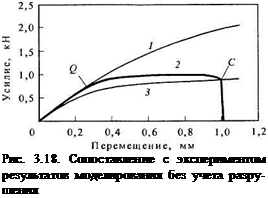При пошаговом моделировании нагружения образцов без учета их разрушения расчетная машинная диаграмма 1 совпадает с эксперименталь­ной 2 на начальном участке, а на завершающем проходит выше (рис. 3.18). Характер поведения экспериментальной кривой, наличие на ней отсутст­вующих на расчетной кривой горизонтального и спадающего участков объ­ясняется ростом трещины. Следовательно, моментом страгивания трещины можно считать точку Q расхождения кривых 1 и 2. Такой способ определе­ния момента страгивания трещины при обработке результатов испытаний на вязкость разрушения представ­ляется более обоснованным, чем определение по измене­нию наклона кривой (как ре­комендовано в стандарте), так как искривление машинной диаграммы не обязательно вы­звано разрушением. Кривая 1 также изменяет наклон, хотя построена для случая постоян­ной длины трещины.

Значение К при страги- вании трещины {Кщ) может

6 — 6705
быть принято в качестве вязкости разрушения (Кс = Kiq) только в случае, если вслед за страгиванием сразу происходит нестабильное разрушение об­разца (обрыв машинной диаграммы). Если нестабильному разрушению предшествует некоторое устойчивое подрастание трещины, то правильнее определять вязкость разрушения после этого подрастания, по последней точке С машинной диаграммы. Однако применение модели, не учитываю­щей роста трещины, становится все менее корректным по мере ее роста. По­грешности можно уменьшить путем введения в длину трещины, наряду с Rp, еще одной поправки, учитывающей ее рост.

Размер поправки должен обеспечить совпадение расчетной и экспе­риментальной диаграмм в точке С (расчетная кривая 3). Более точным яв­ляется постепенное увеличение размера трещины на каждом шаге модели­рования, чтобы расчетная кривая совпадала с экспериментальной кривой 2 на всем протяжении, от начала нагружения до точки С. Найденный в ре­зультате моделирования размер трещины может быть использован для вы­числения Кіс.

Описанная процедура моделирования процесса разрушения требует предварительного определения только деформационной характеристики ма­териала. Увеличение размера трещины в модели производится не на основе анализа НДС, а из условия совмещения расчетной и экспериментальной диаграмм. Как известно, для определения Ки. требуются весьма сложные в изготовлении образцы, а для вязких материалов — к тому же и крупногаба­ритные. Методика моделирования процесса разрушения на основе сопос­тавления пластической деформации металла с его предельной пластично­стью, описанная в разд. 3.2.4, позволяет избежать испытания крупных об­разцов как при оценке возможности нестабильного разрушения, так и при определении критериев ЛМР.

Для моделирования процесса разрушения необходимо обеспечить достаточно мелкую и равномерную сетку КЭ вдоль первых 1... 3 мм траек­тории ожидаемого роста трещины. Методика моделирования включает вы­полнение после каждого шага приращения нагрузки нескольких шагов при постоянной нагрузке, но с учетом изменения геометрии трещины вследст­вие деформирования и разрушения материала КЭ на предыдущем шаге. При устойчивом характере разрушения трещина увеличивается на первых 1—2 шагах после приращения нагрузки, а затем процесс ее роста затухает. Если рост трещины продолжается и ускоряется в процессе выполнения шагов с по­стоянной нагрузкой, то его следует считать нестабильным. Равномерная сетка КЭ необходима для того, чтобы изменение характера роста трещины не было вызвано переходом к элементам другого размера. Мелкая сетка обеспечивает разрушение на каждом шаге сразу нескольких элементов и уменьшает влия­ние дискретности разбивки на конфигурацию фронта трещины.

Как видно из описания методики, речь идет о прямом моделировании процесса разрушения путем уничтожения тех элементов, в которых пара­метры НДС превысили критический уровень, а не о косвенном моделирова­нии путем освобождения узлов КЭ на основе критериев ЛМР, оценивающих зону разрушения интегрально как «черный ящик». Прямое моделирование предоставляет новые возможности при решении задач, но требует повышения точности моделирования НДС на основе учета геометрической и физической нелинейности поведения материала, а также определения новой механической характеристики материала, используемой в качестве критерия разрушения. Основные положения экспериментально-расчетной методики определения этой характеристики, т. е. предельной пластичности материала, и обоснование ее применения в качестве критерия разрушения приведены в разд. 3.2.3, 3.2.4.

Преимущество предельной пластичности перед традиционными кри­териями линейной и нелинейной механики разрушения состоит в том, что это условие разрушения относится к точке материала, а не к зоне, содержа­щей внутри себя острый концентратор. Поэтому условие разрушения зави­сит только от температуры и НДС в точке. Никакое сочетание факторов в соседних точках не оказывает влияния на условия разрушения данной точ­ки, если в ней не изменяется температура и НДС. Это позволяет проводить решение таких «некорректно поставленных» с позиций ЛМР задач, как рас­чет прочности сварного соединения разнородных металлов, в том числе при неизотермических условиях и с учетом обнаруженных дефектов.

Необходимость в большом числе элементов и шагов решения увели­чивает вычислительные затраты на моделирование процесса разрушения сложных деталей. Однако в том случае, когда необходимо дать консерва­тивную оценку опасности внезапного нестабильного разрушения, можно существенно упростить модель. При данной толщине материала такую оценку дает концентратор в виде поверхностной трещины, глубина которой составляет половину толщины сечения, при нагружении по схеме нормаль­ного отрыва. Выполнение условия плоского деформирования в направлении вдоль фронта трещины и нахождение этого фронта в максимальном удале­нии от свободных поверхностей создают максимальную объемность НДС, что приводит к снижению предельной пластичности и максимизирует опас­ность нестабильного разрушения.

Осесимметричная модель сферической оболочки с кольцевой поверх­ностной трещиной в экваториальной плоскости (рис. 3.19) позволяет ис­пользовать двумерные КЭ и свести к минимуму их число за пределами ожи­даемой траектории роста трещины. При этом единственным упрощающим предположением является сохранение осевой симметрии в процессе разру­шения.

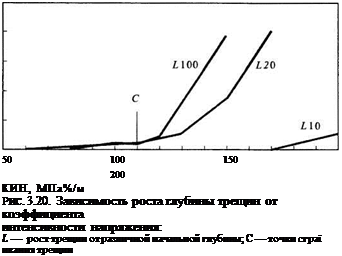
На рис. 3.20 представлен рост L глубины трещины от различных на­чальных значений глубины по мере увеличения внутреннего давления. Размеры оболочки: R = 1700 мм. b = = 200 мм, материал — мартенситно - стареющая сталь 02Х10Н9МТ.

Зависимости роста глубины тре­щины от КИН К получены в результате моделирования МКЭ от исходной глу­бины трещины 10, 20 и 100 мм. Значе­ния Кь при которых наступило страгивание трещин глубиной 20 и 100 мм (если за страгивание принять увеличение глубины на 0,1 мм) практически

совпали и составили 110 МПа%/м. Значения Kh при которых рост этих двух трещин стал нестабильным, также близки (около 160 МПал/м ). Следова­тельно, критическое значение К, найденное для трещины глубиной 100 мм, составляющей половину толщины стенки, применимо и для других толщин и может быть принято за характеристику материала. Значения Ki на момент роста трещины на 0,1 мм оказались близкими к указанной в справочной ли­тературе вязкости разрушения стали 02Х10Н9МТ (Кс = ПО МПа-Ум ). Таким образом, представленная модель сферической оболочки позволяет по имеющимся характеристикам материала (деформационной и характе­ристике предельной пластичности) расчетным путем определять крите­рии J1MP.

Модель позволяет также оценить границы применимости ЛМР для конкретных условий. Из рассмотренного примера ясно, что внезапное раз-

S 2,5

S

3 2,0

К

I 1,5

Си

н

х 1,0

к

IО

£ 0,5

f-

н

о

Z о

рушение оболочки из стали 02Х10Н9МТ толщиной 200 мм возможно при глубине трещины не только 100 мм, но и в интервале 20... 100 мм. Характер роста трещины от исходной глубины 10 мм, также представленный на рис. 3.20, существенно отличается от более глубоких трещин в связи с тем, что страгивание этой трещины происходит при более высоком давлении и после начала общей текучести оболочки. На основании этого можно сделать вывод, что если внезапное разрушение от трещины глубиной 10 мм и воз­можно, то произойдет оно при значении Кь существенно превышающем Кс. Таким образом, для данной оболочки граница применимости ЛМР прохо­дит между размерами глубины исходной трещины 10 и 20 мм. Продолжив численные эксперименты, можно установить характер поведения трещин с исходной глубиной 100...200 мм, влияние толщины материала, его марки, формы исходного концентратора и т. д.

После проведенной проверки применимости и оценки точности расче­та по ЛМР такой расчет может быть рекомендован как более простой взамен моделирования процесса разрушения при проведении большого количества расчетов типовых элементов конструкций. Проверка может служить осно­ванием для ограниченного применения ЛМР даже в том случае, когда не выполняются формальные признаки корректности критериев ЛМР. Следо­вательно, ЛМР может служить «инженерной» реализацией более универ­сальных методов моделирования процесса разрушения.

Еще одна возможная область применения имеющихся данных по кри­териям ЛМР для вязких материалов — уточнение диаграммы пластичности в области высокой объемности НДС. Обычные образцы с надрезами не все­гда обеспечивают разрушение при высокой объемности НДС даже при весьма остром исходном надрезе. В то же время регистрация данных в про­цессе роста трещины в экспериментальном образце связана с рядом методи­ческих трудностей. Имея результаты испытаний стандартных образцов на вязкость разрушения, можно провести моделирование этих испытаний на ЭВМ и уточнить характеристику предельной пластичности так, чтобы обес­печить совпадение расчетной машинной диаграммы с экспериментом. К на­стоящему времени накоплен значительный объем экспериментальных дан­ных по предельной пластичности материалов, в том числе при высоких и низких температурах, но, как правило, отсутствуют данные для высокой по­ложительной объемности НДС.

Таким образом, можно предложить два метода проверки возможности и необходимости применения критериев ЛМР для конкретной конструкции:

1) на основе сопоставления НДС у концентратора, описываемого ЛМР, с точным решением, полученным с помощью МКЭ. Необходимыми характери­стиками материала для оценки погрешности ЛМР являются деформационная характеристика и ориентировочное значение вязкости разрушения;

2) на основе моделирования процесса разрушения и установления ха­рактера разрушения. Требуется деформационная характеристика и характе­ристика предельной пластичности, вязкость разрушения может быть найде­на по ним в процессе моделирования. Применение ЛМР актуально для тех конструкций, разрушение которых может стать нестабильным.

Есть и третий, традиционный способ — испытание крупногабаритных образцов. В этом случае моделирование испытаний позволяет ввести по­правку на устойчивый рост трещины перед нестабильным разрушением.

Накопленные справочные данные по критическим значениям пара­метров ЛМР могут иметь следующие области применения:

1) разработка инженерных методик расчета для тех интервалов изме­нения параметров конструкции, для которых возможность и необходимость применения ЛМР была установлена на основе моделирования МКЭ;

2) проверка и уточнение значений характеристики предельной пла­стичности при высокой объемности НДС. Эта характеристика затем может быть применена для расчета любых конструкций из данного материала, как допускающих, так и не допускающих применения ЛМР.