Будем считать, что граница свариваемого изделия адиаба­тическая, т. е. тепловой поток через границу отсутствует и выполняется условие (3.3). Выполнить это условие можно, поль­зуясь следующим формальний приемок. Нагреваемое изделие ко­нечных размеров представляют в виде бесконечного тела, бес­конечной пластины или бесконечного стержня, для которых из­вестны решения уравнения теплопроводности. Это расширенное тело заполняют системой источников теплоты, для которых гра­ницы конечного тела были бы плоскостями симметрии. На плос­костях симметрии сумма всех тепловых потоков равна нулю; эти плоскости являются адиабатическими, т. е. выполняются гранич­ные условия (З. З'ї. Такую систему источников можно построить для тел, ограниченных параллельными или взаимно пергтендику - лягшьг’и плоскостями: для параллелепипеда, прямоугольной

пластины, стержня конечной длины и др. Все источники, за ис­ключением одного, действующего в реальном теле, ЯВЛЯЮТСЯ фиктивными.

Таким образом, в теле конечных размеров температура в любой точке от действующего источника теплоты определяется рядом, представляющим собой сумму значений температуры от действительного и фиктивных источников в бесконечном теле:

где K, гс, і,и - координаты рассматриваемой точки

в местной системе координат каждого источника; ц ,к - номер источника в направлении х, у,& (за начало отсчета 0,0,0 принимается действительный источник). Ряд (3.24) является, как правило, быстрорасходящшся и для реальных тел учитыва­ются всего несколько членов ряда.

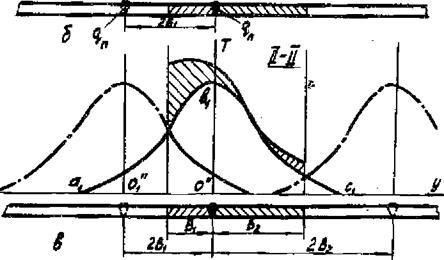
Рассмотрим случай сварки относительно узких полос (ти­повой случай при изготовлении сварных балок). Пусть произво­дится сварка встык двух полос разной ширины, В, + Ьг=Б (рис.3.7,а). Построим распределение температуры в сече­нии 1-І, рассчитанное в предположении отсутствия ограничи­вающих кромок, т. е, полагая пластину неограниченной. Это распределение (кривая аЪс рис.3.7,6) показывает, что влия­нием правой кромки можно пренебречь (на ней тепловой поток отсутствует, £^ = - А. ЭТ/9у-О), в то время как учет левой кром­ки необходим ( ). Расположим симметрично плоскости

у--В, в точке 0, фиктивный источник с той же погонной энергией. Сумма встречных потоков от двух источников равна нулю, т. е. выполняется граничное условие на левой кромке. Те­перь распределение температуры в сварном изделии будет опре­деляться двумя источниками: dbc. от действительного и ctj от фиктивного. Полученное таким образом распределение темпе­ратуры gbt удовлетворяет граничным условиям на кромках. Из ряда (3.24) учтены первые два члена: ] = 0 и j = -I (в слу­чае неограниченной по длине пластины суммирование по і и к, т. е. в направлении х к х. , отсутствует).

На свойстве симметрии границ свариваемого изделия в си­стеме источников основан метод отражения. Из рис.3.7,б видно, что кривая cLf является зеркальным отражением кривой ad. .

к ее оси перемещается источник теплоты. Характер распределе- ния температуры по поверхности полосы при нагреве ее мощным быстродвижущимся линейным источником теплоты (рис.3.8,а) позволяет выделить три области (ряс.3.8,б): 1) область Vs_ , непосредственно примыкающую к источни- ку, в пределах которой боковые границы не оказывают влияния на процесс распространения теплоты; . 2) переходную область, в пределах которой тем- пература практически выравнивается по ширине и тепловой по-

ток из двумерного переходит в одномерный;

3) область V< , в пределах которой температура, одинако­вая по ширине полосы, постепенно попинает - ся вследствие тепло­отдачи в окружающую среду.

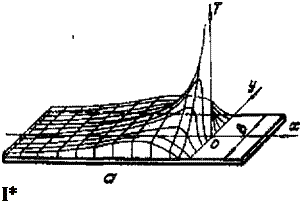
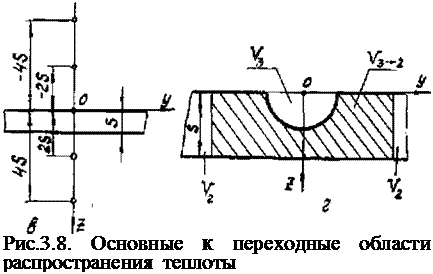
Рассмотрим те­перь случай наплавки валика на неограни­ченный по длине и ши­рине лист большой толщины. Этому случаю соответствует расчет­ная схема плоского слоя, по поверхности которого перемещается точечный источник теп­лоты (рис.3.8,в). Адиабатические усло­вия на поверхностях *.= О и «.=& выполня­ются ( 0), если

так, чтобы эти поверх­ности были, плоскостями симметрии. Тогда температура в плос­ком слое определится аналогично уравнению (3.24):

іУк i^k) ^V(3C'>yia'+‘-KS^

Vf=-oe

Характер температурного поля в плоском слое позволяет также выделить три области (рис.3.8,г):

1) область Уъ вблизи источника, в пределах которой температура не отличается от распределения в полубесконечном теле;

2) переходную область, в пределах которой проис­

ходит постепенное выравнивание температуры по толщине плос­кого слоя;

3) область, в которой теплота распространяется как

в неограниченной пластине от линейного источника теплоты. Обобщим результаты и рассмотрим общий случай распро­странения теплоты в теле с учетом ограниченности его разме­ров по толщине и ширине, При распространении теплоты от подвижного точечного источника в полосе значительной толщины ' плоском слое ограниченной ширины), можно выделить три основ-, ные области - V, tVj,,V4 и две переходные - я »

характеристики которых были даны вше. В зависимости от раз­меров сечения полосы и положения оси перемещения источника теплоты указанные области могут иметь различную протяжен­ность. Более того, иногда некоторые из этих областей вырож­даются. Однако нет необходимости предварительно решать воп­рос, к какой области относится та или другая точка полосы, "ля любой ее точки расчет температуры выполняют по уравнению

где к4,т5 - коэффициенты, учитывающие ограниченность из­

делия по толщине, определяются по рис.3.9; квтв - коэффи - циенты, учитывающие ограниченность изделия по ширине, опре­деляются по рис.3.10, где приведены их значения для оси шва; Тъ- рассчитывается по уравнению (3.13) или (3.15); Тг - по уравнению (3.13) или (3.16); Tt - по уравнению (3.14) или (3.17). Коэффициенты определяют, по какому варианту - (а), ' (б) или (в) уравнения (3.26) - следует выполнять расчет. Тая, например, если при определении коэффициента, учитывающего раз­мер изделия по толщине (по рис.3.9) по условиям задачи попа­дают в правую область, т. е. получают значения коэффициента ms, а при определении коэффициента, учитывающего ограни­ченность изделия ко ширине (по рис.3.10), - в левую, т. е. получают значения коэффициента кь, то температуру рассчи­тывают по уравнению (3.26) (б). Таким образом, влияние'

ограниченности размеров изделия по толщине и ширине на про-

Xs Батовский К. М. Особенности распространения тепла в плите гг подвижного источника. - физика к химия обработки ма­териалов, 1967, ” 5, с. й?-Зо; Определение температуры и ско юстк охлаждения металла шва. - Автоматическая сварка, 1963, 5, с Л-5.

цесс распространения теплоты при сварке характеризуется про­изведением коэффициентов Kg или ms на кв или тъ в сме­шанной по индексу комбинации. Из уравнения (3.26) видно, что оно, как частные случаи, описывает процессы распространения теплоты в полубеоконечном теле ( !<е= ) в неограниченной пластине ( кэ= ) и стержне im%- тБ= О, а также в плоском слое (к5;Н, къ= і или,,тв = 4 ) и ограниченной по ширине пластине (т4=4 , кй>4 или ms=4 ), Анализ

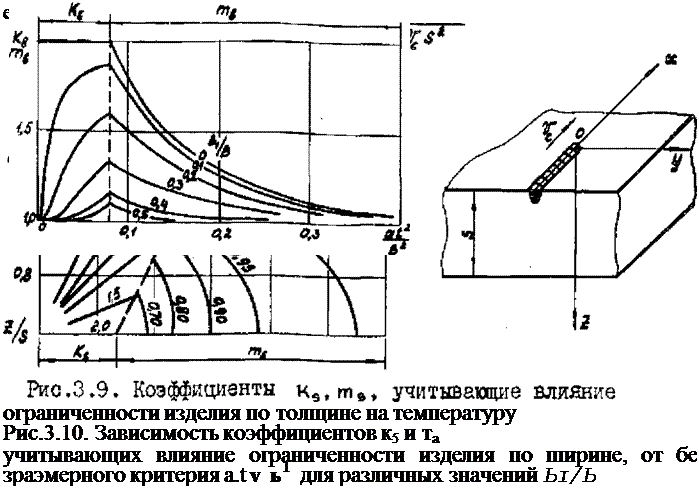изменения коэффициентов к її m позволяет заключить, что при значениях г-/х*+у* ucsVol и г,^0,5s процесс рас­пространения теплоты идет как в полубесконечном теле (об­ласть Уъ ), при значениях г>0,^ *trtзг/а - как в неограни­ченной пластине (область Va ), а при значениях ixl>0p4rcBa/ci - как в стержне (область )*

Удобство изложенной методики оценки температуры заклю­чается не только в том, что не нужно заранее устанавливать, к. какому типу тела (или области V ) относится в данный момент свариваемое изделие, но и в том, что автоматически производится одновременный учет конечных размеров тела как по толщине, так и по ширине.

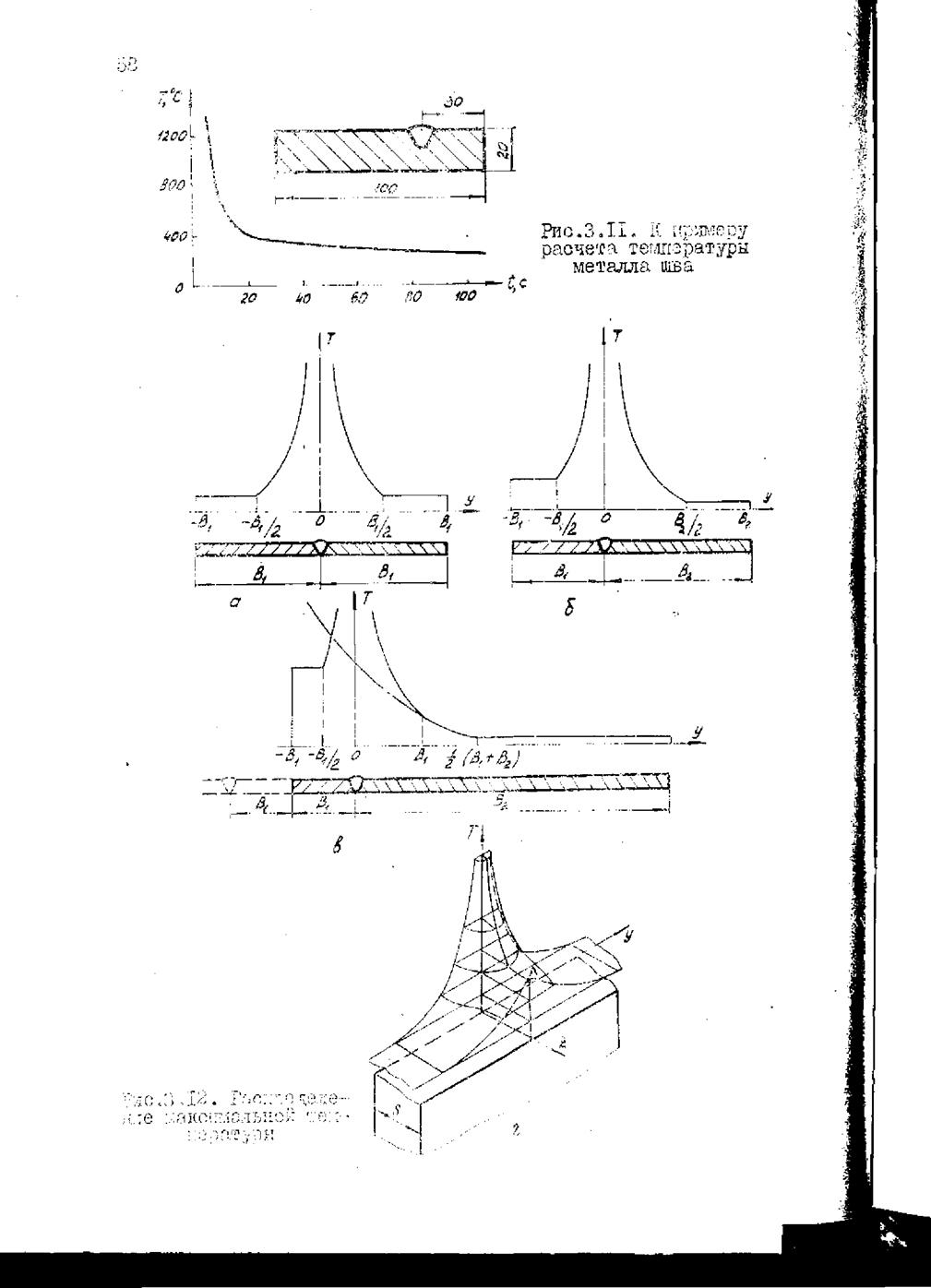
Пример, На стальную полосу сечением В-s =

---- 100x20 мм наплавляют валик на расстоянии 30 мм от кромки. Мощность источника теплоты 8330 Вт. Рассчитать темпера­туру оси шва через 5, 10, 15, 20, 40, 60, 80 и 100 с после прохождения чеоез нее источника ( = 0,417 Вт/см°С, olT = * 0,0033 Вт/см2оС).

Для оси шва у = 0 и г. - 0. Поэтому /зса+ у3- =-х= vtt и, следовательно, а /жг+у4/(тг^2-) == at /зг •, к/s =0 .

Искомые значения температуры, а также опре делящие их

вспомогательные величины приведены в табл.3.1, из которой ясна также последовательность выполняемых операций. .

График термического цикла металла шва, построенный по результатам расчета, приведен на рис.3.11.