Для определения коэффициента трения Cj введем отношение

* = «ус^) Re~,

где Cj - значение локального коэффициента трения при данных усло­виях течения; (у - значение коэффициента трения при изотерми­ческом (безградиентном) обтекании плоской непроницаемой стенки.

Индекс Re указывает на то, что сравнение производится при оди­наковых значениях характерных чисел Рейнольдса, вычисленных по толщине потери импульса. Величина Ч* может бьггь определена из вы­ражения

(4.5)

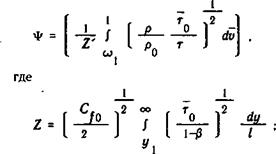(4.6)

- координата нижней границы турбулентного ядра потока; оо( = = «|/«0 - безразмерная скорость на этой границе; г - напряжение трения; т = т/т - закон распределения касательных напряжений по

СТ

толщине пограничного слоя; - то же для изотермического течения; / - длина пути перемешивания; у - поперечная координата; и, pQ - значения скорости и плотности потока вне пограничного слоя; т -

СТ

напряжение трения на стенке.

Коэффициент 0 характеризует влияние пульсаций плотности на пе­ренос количества движения:

^ t * * *

Л v<u Т >+<и v Т > /Л „V

& =------------ —-------------- . (4.7)

<и v >Т

где и, и - составляющие скорости, параллельная и перпендикулярная поверхности стенки соответственно. Штрихом обозначены пульсаиион - ные величины, знаком < > - корреляционный момент.

В условиях развитой турбулентности при Re —► оо выполняются со­отношения со -> 0, 0 -> 0, z -> 1 и уравнение (4.5) имеет пре­дельную форму

I __ - f

I rfcj - (4.8)

о

Предположим, что этот предельный случай, так называемый пре­дельный закон сопротивления, в условиях плазмотронов реализуется уже при конечных значениях числа Рейнольдса. Обоснованием такого

предположения могут служить экспериментальные данные, свиде­тельствующие о сильной турбулизации потока в зоне разряда, а также наличие сильной турбулентности течения из-за шунтирования дуго­вого разряда, разрушающего ламинарный подслой или нарушающего устойчивость ламинарного подслоя. Тогда формула (4.8) может быть использована для определения величины 4* при известных законах р/р0 и г/г0.

Профиль касательных напряжений в пограничном слое аппроксими­руется кубической параболой

т = т/т = і4 + АЛ * а/ * а/,

ст 0 1 2 3

где 5 = у/8, а 8 - толщина динамического пограничного слоя. Коэф­фициенты А - А находятся из граничных условий. Из определения

U О

динамического пограничного слоя и условия плавности в точке 5 = 1

имеем т = О, |Эг/Э£| = 0, а при 5 = 0 величина г = 1. Уравнение

движения в проекции на ось х с учетом малости электродинамических сил за пределами области электропроводности имеет вид

Таким образом, можно записать t/tq = 1 + Л£Ф(£),

где

Ф(*> = (2? + 1)"'. (4.13)

Значение функции Ф(5) меняется от 1 при 5 = 0 до 1/3 при 5=1. Оценки показывают, что в представляющем практический интерес диа­пазоне изменения параметров в условиях плазмотронов Л = 0,1.

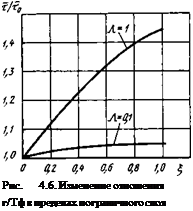
График г/Гф = /(5) показан на рис. 4.6 для Л = 0,1 и X = 1.

Даже при Л = 1 принятие условия т = rQ ведет к максимальной по­грешности в определении касательного напряжения в области 5=1, равной почти ЗО %; при Л = 0,1 эта погрешность составляет лишь

около 3 %. Поэтому в дальнейшем принято т = т^.

Вычислим отношение p/Pq - Для этого введем безразмерную энтальпию

Л= (Л-Л )/(h - Л ) (4.14)

ст 0 ст

и обозначим Аф = (h - h )/ht (4.15)

0 ст 0

где Л, Л - значения энтальпии на стенке и за пределами ст 0

пограничного слоя (в ядре потока) соответственно. Тогда отношение может быть записано в форме

р/р0 = 1/(НАф * 1 - Аф). (4.16)

Будем считать, что распределение скорости и энтальпии в пределах теплового пограничного слоя подчиняется степенным законам

<*) = u/uQ = (y/sf; h = {y/bj)7. (4.17)

Предполагая существование подобия профилей скорости и энтальпии в тепловом пограничном слое, т. е. п = tij, ы = Л, из формулы (4.9) получим

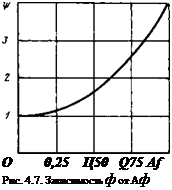* = {-^[1-0 - А*)0,51}2. (4.18)

При Аф -> О Ч* -> 1; при Аф -> 1 4* -* 4 (рис. 4.7).

Введем величину

4* =(St/StJ, (4.19)

^ о Л **

Re-,

где St = а /р и (ЛЛ - Л ) - значение локального числа Стэнтона ст 0 0 0 ст

при данных условиях течения; StQ - то же, но при изотермическом

* *

безградиентном обтекании непроницаемой стенки. Индекс Re-, указы­вает на то, что сравнение производится при условии одинаковых значений характерных чисел Рейнольдса.

Определим выражение для 4^. Из оценок, выполненных в разд. 4.1,

следует, что тепловой поток определяется конвективным теплопере - носом. Можно показать, что

q = р <v h >(1 - (4.20)

Величина характеризует влияние пульсаций на перенос теплоты:

'о ' '2

л v<h?+<v h?

Здесь y^j - поперечная координата границы ламинарного подслоя;

- значение безразмерной энтальпии при у = - безраз-

мерный тепловой поток при изотермическом безградиентном обтекании непроницаемой стенки.

В условиях развитой турбулентности при Re -» оо выполняются ус­ловия Л| —*• 0, —*• 0, Zj, —*■ 1 и уравнение (4.25) имеет предель­

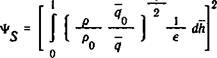ную форму

Будем предполагать, как и ранее, что этот предельный случай, так называемый предельный закон теплообмена, в условиях плазмотронов реализуется уже при конечных числах Рейнольдса.

Для определения Фд необходимо знание законов изменения p/pQ и

Qq/Q - Изменение р/р0> как было показано выше, описывается форму­лой (4.16).

Найдем теперь соответствующую зависимость для q /q путем ап­проксимации профиля плотности теплового потока исходя из следующих граничных условий; при tj. = 0, q = 1 bq/btp = 0; при ^ = 1, q = = 0 bq/btj. = 0. Этим условиям соответствуют аппроксимирующая формула

q = 1 - 3^ ♦ (4.28)

и закон

fq = К (4.29) справедливый при отсутствии вдува и энерговыделения в пограничном слое объемными источниками теплоты.

После подстановки выражений (4.16) и (4.29) в (4.27) находим

		Г — 11
II	2 м»	і - (і - т 2

Следует обратить внимание на то, что при расчете числа Стэнтона необходимо учитывать влияние закрутки потока под действием враще-

I 2 2

ния дуги. В формулу (4.21) следует подставить = чи ♦ w, где

и - средняя продольная скорость, aw - некоторая средняя танген­циальная скорость газа. Последняя может бьггь приближенно оценена из уравнения баланса моментов, действующих на поток в плазмотроне,

(4.31)

где / - сила тока; В - индукция внешнего магнитного поля; L - длина межэлектродного зазора; D - некоторый средний диаметр вра­щающейся массы газа; - диаметр дуговой камеры; G - расход газа

через плазмотрон; S = nDJ - площадь соприкосновения газа со стен­ками канала (/ - длина камеры); - коэффициент трения газа о

стенки канала; £ - коэффициент, учитывающий влияние изгиба дуги в плоскости ее вращения.

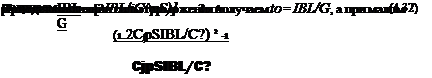Левая часть уравнения (4.31) описывает момент, передаваемый газу при вращении дуги; первый член правой части - момент коли­чества движения* приобретаемый газом, второй член - момент трения газа о стенки электродуговой камеры. Полагая £ = 1 и D * D,