Применяемый выше метод опреде­ления деформаций и напряжений сво­бодной полосы может быть исполь­зован и в тех случаях, когда полоса закреплена или имеет большую тол­щину.

Так, например, если ограничить деформации полосы соответствую­щими закреплениями, лишив ее воз­можности изгибаться и допуская лишь продольные деформации, то прямая Д займет горизонтальное положение. Это означает, что относительное удли­нение волокон остается одинаковым на всей ширине полосы. В случае, когда температура нагрева полосы нигде по ширине не превышает 500°, эпюра относительных деформаций бу­дет иметь вид, изображенный на рис. 28, а. В этом случае положение прямой Д определяется только одним условием, а именно: соблюдением ра­венства нулю суммы всех внутренних сил. То, что при этом внутренние силы будут создавать момент, не имеет значения, так как он будет воспринят закреплениями полосы.

В том случае, когда нагрев в не­которой зоне достигает температур, превышающих 600°, эпюра относи­тельных деформаций будет иметь вид, представленный на рис. 28, б. В этом случае в зоне, нагретой свыше 60)°, упругие деформации су­ществовать не будут.

Положение прямой Д определится из следующего равенства:

Л

— (Уз — У*) —Y &s 0;2 — Л) + і(Л — х) йу = °>

откуда после преобразования получим

д = [тЛ--Vi)+j >4у].

Уз

Соответственно при остывании эпюра деформаций предста­вится в виде, приведенном на рис. 28, в.

В тех случаях, когда имеет место неравномерный нагрев не только по ширине, но и по толщине полосы (например наплавка валика на часть кромки толстого листа), может оказаться, что область температур, превышающих 600° (область пластического состояния металла), будет занимать лишь часть толщины листа, тогда как остальная часть толщины будет находиться в упругом

Рис. 29. Схема для определения деформаций толстой полосы при наплавке на кромку.

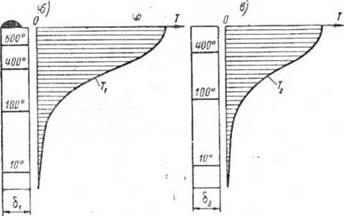
состоянии. Если распределение температуры по толщине листа имеет вид, приведенный на рис. 29, а, то можно мысленно раз­делить рассматриваемый лист на два более тонких листа тол­щиною Sj и &2 и принять в каждом из них равномерное распреде­ление температуры по толщине.

Распределение температуры по ширине каждого из двух рас - сматриваемых листов может быть представлено кривыми, пока­янными на рис. 29, б и в. Соответственно представленным кри-1 мим распределения температур могут быть построены кривые относительных удлинений отдельных волокон обоих листов и предположении независимости удлинений каждого волокна от других волокон. Характер распределений относительных тепло - мых удлинений Xj и Х2 обоих рассматриваемых листов предста - илен на рис. 30.

Так как влияние, оказываемое отдельными волокнами друг ил друга, приводит к линейному распределению относительных действительных деформаций, а взаимная связь обоих листов — к общности действительных деформаций, то действительные де­формации обоих листов изобразятся прямой Д, справедливой как для листа так и для листа толщиною 32.

Положение прямой А определится из условия, что сумма всех внутренних сил в обоих листах должна равняться нулю, и сумма моментов этих сил относительно любой точки так же должна быть равна нулю.

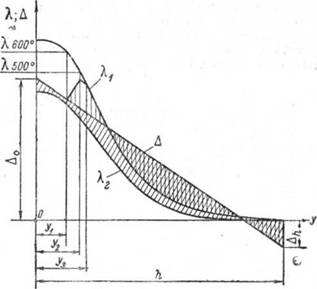
Рис. 30. Относительные деформации толстых полос.

В случае, представленном на рис. 30, основные условия рав­новесия могут быть написаны в следующем виде:

si j (Лу—) dy 4- 4"Су з —Ух)4- е, (Уз - з>2)514- ■,

А

+ f (A^—X2v) dy = 0;

‘o

h l‘o

j (Д> — )ydy + ~2% (y2 —Уі) [Уі - f (y2 —4- } (4)

Л y

4" es (Уя. У 2) [Уг 4 2“ (Уз —У2) ] ^1 4“

А

+ )ydy = 0.

о

Дополнительным является условие:

и,- (5)

Если обозначить:

Л

f Ау dy = FJ; f Aydy = Fnn ;

o Vs

j byydy = ; j. &yydy =

O v3

ft ft

$МУ“ф*л; fb-dy-ty,;

V. О

®j (^2 — ) = /l ; e, (y, — дг2 ) = /2 ;

4-®Л^2— л)[^і +-§-(у«—Уі)] = «х; е, СУз —У2) ^2 +-J- Ob —У2 )j =т2, то после некоторых преобразований получим

*./% + **?-Ф? Л+ФІ-Л-Л; ,

Si ж; +82AI? = 3Kf +5ВЙ — m, — m2 . (b)

У* u *уа 1 >

С другой стороны, левые части приведенных уравнений можно выразить в следующем виде:

81^ + 82Я0 = 4-Д0|[г1(Л + Л)±р - + 52А ]„ +

8, Л» + 8.Л1* = -1- Д0 {[8, (А - Л) 2 (Л +Л + +

-|- 2 S2 А - *|а - f - о, (Л —л) (Л —_уз - f-8» Л - | •

Из условия равенства левых частей уравнений (f) и только что приведенных получим для А0 следующие выражения:

д _________________________ 2(ф-*.+ф4'~/,~Л>________ . (7)

[®1 ~~л* (ft +Л) + М ]а +8, <*-А>*-+Ц ft '

д________________ 6 ^.?.+ Ч -”»-”■«>__________________ (Г)

J ^1 д ~ (ft5Л_>'з-(— _Уз ) -f-8g ft3 j ^™-!(ft""bft^s?_у3 “b^aft )

Из совместного решения обоих уравнений для Д0, обозначая

фЪ, + Фі-И

Л Г S, fcMi-l - Во АІ -2 f Л Го. -4- Л Vo — 2 V2^ 4- Ui^ ,(9)

^1*. + Щ0 —r>h—m.,=. [М], (8)

6 [УИ]		-2[F]			1
4[F]|	I8"	(* Л) (Ла + АУз+Дф + М2 h з |	|—6[АГ]|	[8і»=*(Л+Л)+М

получаем

Задаваясь значениями з/g и вычисляя величины [F] и [М], поль­зуясь уравнениями (8), из выражения (9) определяем величину а', после чего могут быть определены величины Д0 [из уравнения (7) или (7')] и Дй = а'Л0.

Зная величины Д0 и ДЛ, определяем величину Д_у3 и проверяем, удовлетворяется ли уравнение (5). Если уравнение (5) не удо­влетворяется, то, задаваясь новым значением _у8, повторяем рас­чет в прежнем порядке.

Когда положение прямой определено, то становятся извест­ными для данного момента времени и общие деформации (кри­визн?) полосы и местные относительные деформации и напря­жения в обеих частях (по толщине) рассматриваемой полосы.

Определение деформаций и напряжений при последующем остывании после наплавки может быть определено совершенно таким же способом, как и в случае равномерного распределения температуры по толщине листа.