ОЦЕНКА УРАВНЕНИЯ ДЛЯ КОЭФФИЦИЕНТА ТЕПЛОПЕРЕДАЧИ И КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПОВЕРХНОСТИ НАГРЕВА
 3 июня, 2013
3 июня, 2013  admin
admin |
(755) |
![]() Если в уравнении (698) обозначить числитель через и и знаменатель через р, то уравнение, определяющее коэффициент теплопередачи регенераторов, будет выглядеть следующим образом:
Если в уравнении (698) обозначить числитель через и и знаменатель через р, то уравнение, определяющее коэффициент теплопередачи регенераторов, будет выглядеть следующим образом:
Здесь
|
С • в • 7 2аг • V п |
|
И — |
|
||
|
||
|
||
2ягтг. п
|
1,051^1 |
|
X |
|
(1-е |
|
С • в • Т 2 • аг • тг. п |
_ 2 аг тг. п
1,05— С ' 8 ' ~Г— (1 — е С [194]'Т )
2
|
(756) |
![]() ‘ аг ■ тг. п
‘ аг ■ тг. п
|
1+0,1 |
![]() С в Ч 2аг • V п
С в Ч 2аг • V п
2агтг
С В.-і |_ 2 • “г • ,гг> „
|
4 • с • з • у |
![]()
|
-1 |
![]() X (1-е в-т. /1 +
X (1-е в-т. /1 +
|
(757) |
![]()
|
4 • с ■ в ■ у |
4 • і)
Фактор — в уравнении (755) указывает на ухудшение, которое претерпевает идеальный коэффициент теплопередачи вследствие недостаточной теплопроводности и аккумулирующей способности кирпича. Этим отношением будет характеризоваться коэффициент полезного действия поверхности нагрева &пов. Следовательно,
|
^)пов |
![]() <758)
<758)
'•ид
Или по уравнению (755)
(759)
Коэффициент полезного действия является, следовательно, отношением действительного коэффициента теплЬпередачи регенератора к коэффициенту теплопередачи такого ^ке регенератора, но
25 А. Шак
С бесконечно теплопроводными, бесконечно большой ТОЛЩИНОЙ
Кирпича (то же, что и идеальный регенератор второй степени).
Оказывается, величина и является лишь функцией критериев
2 Яр • ^г. П Д &г + Д &в - Г
---- -—— и —-—-— ----------------- , следовательно, может быть выра-
С-а-1 ^г. ср — ^в-ср
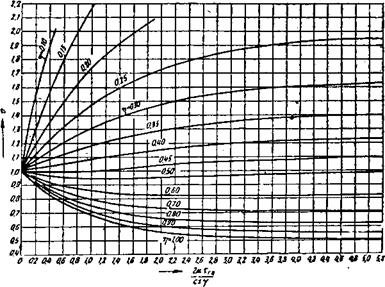
Жена в форме пучка кривых. Функция О зависит от критериев
—— * Тг, п и п. Следовательно, она так же может быть выражена с • 5 • 7
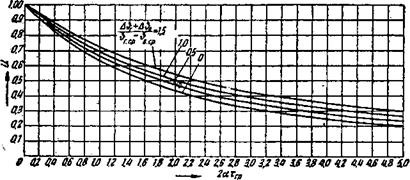
Пучком кривых. На рис. 62 и 63 даны функции и и V, следова-
|
Рис. 62. Функция и |
Тельно, их значения могут быть определены непосредственно из этих графиков. Влияние изменения температуры воздуха + газа + Д в в соответствии с рис. 55 довольно незначительно* В большинстве случаев можно пользоваться приближенным значением
£?Г.+-4Ь—=0,5.
(.1 Л
1 г. ср ср
При выводе конечного уравнения (698) играло роль значение п, которое при отсутствии точных измерений было принято равным 8 (см. уравнение (627) и рис. 57]. Если решить уравнение (697) при определенных нормальных условиях для различных значений п, то получим следующие данные:
П Коэффициент полезного
Действия поверхности
Х/хид
2 TOC o "1-5" h z 0,864 *
4 0,844
10 0,825
Со 0,811
Анализируя эти величины в зависимости от п, найдем, что в рассматриваемой области п (между 6 и 10) наблюдается лишь
Небольшое изменение равное примерно 1%. Следовательно»
*ИД
Выбор значения п = 8 не связан с большой ошибкой.
|
Рис. 63. Функция в |
Поразительный результат показывает анализ уравнения (698) для различных толщин кирпича! Если принять следующие значе - йия для регенератора:
Удельная теплоемкость кирпича............................ с=0,25 ккал/кг, °С
Объемный вес кирпича.......................................... 7=2000 кг/ма
Коэффициент теплоотдачи.................................... аг=ав=20 ккал/м*•
■час-*С
Продолжительность половины периода. . тг. П = тв. п = 1 час
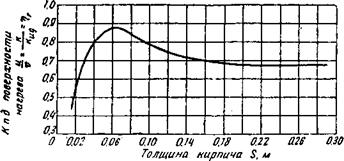
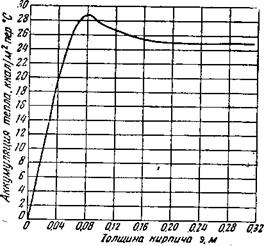
То для различных толщин кирпича получаем коэффициент полезного действия поверхности нагрева ^„ов. который графически изображен на рис. 64. Видим, что при тонких кирпичах (толщи-: ной до 40 мм) коэффициент полезного действия поверхности на - . грева с увеличением толщины кирпича растет очень сильно. При толщине кирпича между 50 и 70 мм достигается ясно выражен-. ный максимум. Затем с дальнейшим увеличением толщины кирпича происходит сначала быстрое, потом более медленное сни-. 25* женшГ коэффициента полезного действия поверхности нагрева и в конце он полностью становится независимым от растущей толщины кирпича. Автор пока не видит физического объяснения столь неожиданной зависимости, так как прежде всего казалось бы надо предположить, что коэффициент полезного действия поверхности нагрева с увеличением толщины кирпича должен приближаться к предельному значению — максимуму. Такое предельное значение, согласно рис! 64, получается, разумеется, для
Частного отношения — при бесконечно большой толщине кирпича. Но странно, что это предельное значение не является мак-
|
Рис. 64. Влияние толщины кирпича на коэффициент полезного действия поверхности нагрева */*Ид |
Симальным. С этим пожалуй, так же связана формула Хаузена, из которой сразу видно, что коэффициент полезного действия поверхности нагрева будет тем больше, чем тоньше кирпич (см - стр. 349).
Следовательно, количество тепла, отдаваемое или восйрини- маемое кирпичом в регенераторе, не увеличивается с увеличением толщины кирпича, а достигается при продолжительности периода. в 2 часа и нормальном шамоте максимума при толщине кирпича в 50—70 мм, чтобы затем снова уменьшиться. При более коротком периоде эта, самая благоприятная толщина кирпича уменьшается, а при более длительном — увеличивается.
Степень использования кирпича. В уравнении (600) степень использования кирпича уже определялась как отношение изменил температуры поверхности к изменению средней температуры кирпича за период. Если кирпич характеризуется бесконечно высоким коэффициентом теплопроводности X и соответствующим ему коэффициентом температуропроводности а, то изменение температуры поверхности полностью совпадает с изменением температуры по всей массе кирпича. При этом степень использования кирпича равна 1. Если же коэффициент теплопроводности кирпича равен нулю, то температура внутри кирпича остается постоянной, т.' е. т) = 0. Степень использования кирпича
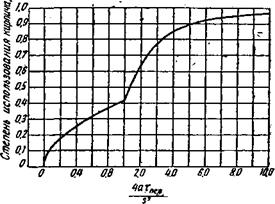
Г] зависит лишь от критерия 4' аТпеР. На рис. 65 дана
Кривая зависимости г) для кирпича толщиной 5 м при двустороннем обогреве, оассчитанная Г. Гребером* для косинусоидального изменения температуры поверхности. По всей вероятности при иных формах изменения температуры поверхности величина т|
|
Л»
Рис. 65. Степень использования кирпича по Греберу |
Не показывает значительных изменений. Если А^ВОв *С — происходящее изменение температуры поверхности за период, т. е.
TOC o "1-5" h z й» = & —в - °С, (760)
Пов пов. макс пов. мин *
То количество тепла, аккумулируемое или отдаваемое 1 м2 поверхности за период при двустороннем обогреве кирпича,
Ф — А'-.* ' V '11 Д8П0В ккал/м2 • пер. (761)
Следовательно, при изменении температуры поверхности на 1°С ф = —--а ' * ' 4 ккал/м2 • пер • °С. (762)
Если рассчитать аккумуляцию для различных толщин кирпича по уравнению (762), подставляя значения, данные на стр_.387 и рис. 65, то получим кривые, изображенные на рис. 66. Здесь также количество аккумулируемого или отдаваемого за период тепла увеличивается с увеличением толщины кирпича до ясно выраженного максимума при толщине кирпича около'80 мм, чтобы затем быстро уменьшиться с последующим замедлением этого уменьшения и стремлением к постоянному значению, которое достигается при толщине около 200 мм. Следовательно, данная кривая аналогична кривой, изображенной на рис. 64 для степе-
|
Рис. 66. Аккумуляция тепла периодически нагревающимся кирпичом (по Греберу) |
Ни использования поверхности нагрева. Но при этом ход кривой на рис. 64 непосредственно не связан с рис. 66. Если указанная величина т) берется не точно по рис. 66, а соблюдается такой, что величина аккумуляции по рис. 66 сохраняет свое максимальное значение и при толщине кирпича больше 80 мм, то все-таки характер кривой аналогичен рис. 64.
Регенератор с неравномерной аккумулирующей способностью. Выше уже указывалось на то, что формулы, выражающие падение температуры воздуха или повышение температуры газа [уравнение (743) и соответственно (724)] не содержат общей аккумулирующей способности насадки, а расчетной величиной является аккумулирующая способность (или водяное число кирпича)
^к — ’|С~ ‘ 5 2 7 ^ ккал/м2-°С в рассматриваемой точке. Как было
Уже сказано выше, это, однако, справедливо лишь в том случае, если участок с высокой аккумулирующей способностью составляет значительную, долю всей поверхности нагрева или, точнее, на этом участке происходит значительная доля всего теплообмена. Само собой разумеется, невозможно существенно уменьшить падение температуры воздуха тем, что, например, в каупере с общей поверхностью нагрева 20000 м2 верхние 100 м2 выложить из кирпичей большой толщиной с высокой теплоемкостью, сле - доватёльно, с высокой аккумулирующей способностью, характеризуемой. Напротив, в горячем конце каупера необходимо, чтобы 2000 мг, т. е. по меньшей мере 10% поверхности нагрева, было с большой аккумулирующей способностью для того, чтобы изменение температуры воздушного потока, поступающего из более холодной части насадки, выложенной тонкими кирпичами, могло бы заметно сгладиться при прохождении потока через поверхность нагрева с большой аккумулирующей способностью.
При этом необходимо учесть, что по уравнению (743) падение температуры горячего воздуха прямо^ пропорционально разности между температурами газ—воздух йьср—9-в. ср в рассматриваемой точке. Эта разность температур в кауперах очень сильно уменьшается на холодной стороне (от 400 до 100°С).
Следовательно, аккумулирующая способность (или толщина кирпича) поверхности нагрева на холодной стороне в этом случае должна составлять четверть аккумулирующей способности на горячей стороне или соответственно ее надо уменьшить на одну четверть, чтобы изменение температуры кирпича не было сильнее, чем на горячей стороне. Это подтверждает также уравнение (743), по которому аккумулирующая способность на рассматриваемом участке (а не во всем регенераторе) является величиной, от которой зависит падение температуры воздуха, так что аккумулирующая способность поверхности нагрева в холодной часта может быть уменьшена еще больше, не вызывая отрицательного влияния на температуру горячего воздуха.
Теперь спрашивается, какую часть поверхности нагрева с более высокой аккумулирующей способностью нужно подставлять при расчете падения температуры по уравнению (743), если эта поверхность нагрева сама составляет лишь малую часть от общей поверхности нагрева. Иными словами, надо определить, насколько влияет вышеназванная небольшая часть поверхности нагрева (100 м2 из 20000 м2) насадки каупера на падение температуры горячего воздуха. Аккумулирующая способность этой ча-
Ст 5 * Т • Т] РЯ1
Сти поверхности нагрева на горячей стороне ------------
Аккумулирующая способность остальной поверхности нагрева Какую же аккумулирующую способность принимать при расчете температурного перепада дутья?
Самое простое — это в качестве расчетной аккумулирующей способности Wkcр принять среднеарифметическую величину. Но
При этом решающую роль играет не только величина части поверхности нагрева, но и величина ее, удельной теплопередачи х •('&г. ср—^в. ср), ккал1м2 • пер. Следовательно, сильное падение температуры, происходящее при омывании наибольшей части поверхности нагрева насадки, выложенной тонкими кирпичами (с малым ), будет затухать и соответствовать более низкому падению температуры, которое наблюдается в последующей части поверхности нагрева насадки, выложенной из болеё толстого кирпича, тем быстрее, чем интенсивнее теплопередача на участке, выложенном кирпичами большей толщины. Поэтому нужно брать не среднеарифметическую аккумулирующую способность из частей поверхности нагрева и ^2*^2» а среднее из значений - Р1 * • XI * (Фг. ср ^в. ср ) 1 И /72* 'И2*( 9-г. ср — ^в. ср )г.
Так как все равно речь идет лишь о приближенном рассмотрении данного вопроса, в дальнейшем необходимо подставлять величину изменения удельной теплопередачи не в количественном выражении, а заменить его соответственно меньшим крайним значением Т7!, выше которого влияние предыдущей поверхности нагрева должно быть компенсировано.
Обычное среднеарифметическое значение водяных чисел (аккумулирующей способности) = - с- ? , которые приме
Нены в уравнении (743), сообразно с вышесказанным было бы равно:
TOC o "1-5" h z Г*ср = + ккал/м* • °С (763)
Или при Р2 = Т7—
И^Аср = Им;- ^--(^1-^2)- (764)
Если удельная теплоемкость с, объемный вес у и степень использования т) постоянны по всему регенератору, то уравнение (764) переходит в
^ср= % ■ (*1 8з) м. (765)
В этих уравнениях
№к1—водяное число рассматриваемой малой части поверхности нагрева с большей или меньшей толщиной кирпича в конце регенератора, ккал(м2 °С;
— водяное число основной поверхности нагрева, ккал/м2-°С
Г*ср — водяное число, которое надо подставлять при расчете в уравнение (743), равное р ‘ **' - ;
Р! —малая часть поверхности нагрева (относится к ЙРЛ); .
М2'
Р,2 — остальная поверхность нагрева (относится к ), м2-, — общая поверхность нагрева, м2;
51, — толщина кирпичей в соответствующих частях поверх
Ности нагрева насадки /ч и Р2, м;
«ср — средняя толщина кирпича, подставляемая в уравнение (743), м.
Но примененный здесь приближенный способ справедлив лишь дл^ малой части поверхности нагрева Р1, так как иначе не будет выполняться условие уравнения (743), сообразно с чем водяное число рассматриваемой части поверхности нагрева решающим образом влияет на изменение температуры газа или воздуха. Это влияние водяного числа будет единственным, если Влияние предшествующей части поверхности нагрева, выложенной например, кирпичом с меньшей толщиной, будет затухать. В ус - . ловиях кауперов и подобных ему регенераторов, отапливаемых
Гг
Газом, у которых ------- <1, компенсация температурных измеие-
Гв
Ний происходит после прохождения потоком 20% поверхности на-
П Гг - ,
Грева. В регенераторах, у которых—->1, эта компенсация про-
У* В
Исходит, пожалуй, лишь после прохождения 25—30% по-
Верхности нагрева (если —— <1—теплопередача в горячей ча-
^ в
№
Сти большая, если —>1 — малая). На основе этих положений
^ в
Можно сделать второе упрощение уравнений (764) и (765), которое основан^ на предположении, что среднее водяное число равно №к1, если часть поверхности нагрева, относящаяся к иРЛ1, составляет приблизительно четверть всей поверхности нагрева. Выбирая ради простоты линейную зависимость, вместо уравнения (764) можно записать выражение
^*ср— ^а — • №к1-Шкг). (766)
Считаем часть поверхности нагрева с соответствующим водяным числом №л1 частью. всей поверхности нагрева Р. Следовательно, можем записать
— Р • Р м*>
Р2 = (1-р)Рм*
И уравнение (766) принимает вид
Й^ср - - (1~р) ^~-3р -/Г-. 0ГИ - фкг)
ИЛИ
Ср = Whl - (1 - Ар). (Wkl - W^) ккал/м* ■ °С. (767)
Отсюда для регенераторов, у которых удельная теплоемкость с, объемный вес V и степень использования rj повсюду одинаковы, средняя толщина кирпича
Scp= Sj — (1 — Ар) • (sx — s2) м. (767а)
В самом деле, в это'м уравнении среднее водяное число или толщина кирпича равно водяному числу соответствующей части поверхности нагрева F в рассматриваемом конце регенератора, если Fi составляет четверть всей поверхности нагрева F, т. е. р = = 0,25. Уравнения (766) и (767) исходят из того, что величина Fi возрастает с введением среднего значения. Если, например, поверхность нагрева Ft составляет лишь 10% всей поверхности нагрева F, то р = 0,10. Если же толщина кирпича Si = 0,050 м, &з = 0,02 м, то
Scр = 0,05 — 0,6 • 0,03 = 0,032 м
Вместо 0,023 м, что получается в результате простого арифметического усреднения по уравнению (763).
Если весь регенератор характеризуется постоянным водяным числом WK2, т. е. р = 0, то уравнения (767) и (767а) снова дают это правильное граничное значение. Если F больше, чем четверть F, следовательно, р>0,25, то Wkcp-Wkl и уравнение (767) неприменимо.
Уравнение (767) также означает лишь приближение к действительности, и точное определение среднего водяного числа — дело дальнейших исследований. Но бесспорно уравнение (767) дает результаты значительно более высокой точности, чем уравнение (764).
Все сказанное справедливо как для Wk, так и для производительности по нагреву или удельной теплопередачи q ккал/м2 час. Сообразно с этим уменьшение удельной теплопередачи близ выхода газового или воздушного потоков приводит к уменьшению во времени температурного перепада а&^или Мв. Но уменьшение q в непосредственной близости от выхода, так же как и увеличение водяного числа поверхности нагрева Wk, приводит к эффективному уменьшению температурного изменения лишь в том случае, если часть поверхности нагрева, на которой совершается это преднамеренное уменьшение теплопередачи, значительна.
Расчет температур в регенераторе. По уравнению (574) для регенераторов с одинаковой или различной продолжительностью периодов нагрева и охлаждения количество тепла, передаваемое за период на 1 м2 поверхности нагрева, составляет
<2 = х. (&г — дв) ккал/мг • пер,
Где х — коэффициент теплопередачи периода. Видна аналогия х с известным коэффициентом теплопередачи регенератора который отнесен к 1 часу.
Здесь мы пользуемся следующими обозначениями:
&г — среднее по времени значение переменной температуры греющей среды (в дальнейшем — газ), °С;
&„ — переменная температура нагреваемой среды (среднее по времени значение), в дальнейшем— воздух, °С;
»г, и-О* —температуры сред на входе (постоянные), °С; ■ . 0г2 и^&г2 — температуры сред на выходе (средние по вре
Мени значения), °С;'
.Р —общая поверхность нагрева, м2;
Рх — текущая поверхность нагрева, считая от входа газа, м2;
Иг —объем газа, проходящий за период (0° С, 760 мм рт. ст.), нм31пер-,
Ув — объем воздуха, проходящий за период, нмг1пер срт и срв— соответствующие истинные удельные теплоемкости, ккал/м3° С;
№Т = УТ- срт — водяное число гаЗа, протекающего за период, ккал/пер°С;
№в — Ув • Срв — водяное число воздуха, протекающего за период, ккал/пер ° С.
Количество тепла, отдаваемое за период нагрева или охлаждения на элемент поверхности нагрева йРх, равно
(!(} = ■*.• (&г — $в) • йРх ккал/пер. (768)
Это переданное количество тепла должно быть равно изменению теплосодержания среды, протекающей через йРх. Если температура более нагретой среды (газа) на своем пути через йРк снижается на величину йЬг °С, то
^==-^г-сРг.^»г
Или
СК2 = — МГГё ккал/пер. (769)
Изменение теплосодержания более холодной среды (воздуха)
6(1= — й<1&л ккал/пер. (770)
Знак минус в уравнениях (769) и Д770) вызван тем, что как температура газа, так и температура воздуха уменьшается в положительном направлении Из уравнений (769) и (770) следует
V »'г V[196] I
Или
• TOC o "1-5" h z = - (77»
Если сюда подставить (Н2 из уравнения (768), то получим
Йхьт-»в)^-^(ьг-ьв).(-±----------------- (?72>
Или, взяв неопределенный интеграл *, получим
1п (&Г_ &в) = _ х (_1-------------- рх + с. (773)
Постоянная интегрирования С определяется из граничных условий: на входе газа ( Рх = 0) разность температур 0Г—&в должна быть равна величине дГ1— дв2; следовательно, по уравнению (773) при Рх = О
1п(вг1-»вг) = С.
Если это выражение подставить в уравнение (773), то
TOC o "1-5" h z *г) (774)
Или после потенцирования
-Х рх ( —---------------------- —]
= г *'в °С. (775)
Теперь по рис. 60 количество тепла, отдаваемое газом до достижения температуры &г (там обозначено йгср), равно
<?г = • (&г1 — &г) ккал/пер (776)
И количество тепла, воспринятое воздухом в интервале температур »в и &в2 ,
<?В = ^в • (».2 - »в) ккал/пер. (777)
Так как мы рассматриваем установившееся состояние, то величины <2 в уравнениях (776) и (777) Должны быть равны. Приравнивая правые части уравнений, получим переменную температуру воздуха
----- ^--(»п-^Х. (778)
Если это значение &в подставить. в уравнение (775), то после решения относительно &г получим переменную температуру газа
■* ш ш )
^ _ Ув • »в, ' (^п '%г)е_______ ^___ в о£ (779)
Г шл—' * '
Это уравнение идентично уравнению (512), выведенному для противоточных теплообменников, только коэффициент теплопередачи & надо заменить на и - Как раньше, так и в дальнейшем, применяя точно такой же вывод и для регенераторов, приходим к тем же самым формулам, что и для рекуператоров. Отсюда следует вывод: распределение средних по времени температур в регенераторе определяется с помощью формул, справедливых для рекуператоров равной поверхности нагрева и аналогичного типа (прямоток или противоток), если вместо коэффициента теплопередачи £ подставлять у. и все количество отнести не к часу, а на период. Идентичность формул распространяется также и на переменные коэффициенты теплопередачи.
Температура кирпича. Для средней температуры поверхности нагрева, т. е. кирпича, как и для других температур, справедливы формулы для рекуператоров. При этом принятую в формулах для рекуператоров единицу времени — час надо заменить периодом и соответственно вместо коэффицентов теплопередачи аг и ав, отнесенных на час, надо брать значения аг • тгл и ав • тв.„, справедливые для периода. Температуру поверхности кирпича можно найти по уравнению (579), если разность температур поверхности в периоды газа и воздуха
|
Пев. ср = V сР - Г ; _ . _В в-п • °С (780) |
![]() " • я • V п + ав • й • ■"
" • я • V п + ав • й • ■"
V п+а1
Здесь Фпов. ср равна средней температуре кирпича и равна средней температуре его поверхности в период газа или воздуха, так как А'б'пов = О.
У кирпичей большой (относительно продолжительности периода) толщины, в центре которых температура остается постоянной, уравнение (780) дает правильное значение температуры цев - тра. В газовый период средняя температура поверхности будет.
На величину выше, а в воздушный период — на й^°в
Ниже, чем указанная температура 8к ср. При этом Д&пов —разность средних температур поверхности в газовый и воздушный периоды, которая играет основную роль при выводе коэффициента теплопередачи и. Следовательно, температура поверхности в газовый период
“Г^г ‘ ТГ. П ~Ь ав'ввтв. п I ^ПОВ о ГУ /'7014
|
Г. пов. ср И в воздушный период |
![]() Г- П0В - С° = 1г-тгп + ав ------------------- + С (?81)
Г- П0В - С° = 1г-тгп + ав ------------------- + С (?81)
Г г. п * в
О " аг • »г • тг. п + °в ^в ТВ. П ^ПОВ ор ПК2
В. ПОВ. ср г. ' '
Удельная теплопередача, или тепловое напряжение поверхности нагрева. Величина <7Г или <7В представляет собой теплопередачу в рассматриваемой точке (тепловое напряжение поверхности иагрева) в ккал/м2 • час. В период нагревания
Q = —-— • (&г— 8В) ккал/мг • час (783)
Тг. п
Или по рекуперативным формулам {уравнения (457) и (458)]
<7Г = ^— • (&г1 — йе1) • f • е Х1'т ' №’в ' ккал/мг • час (784)
Тг. п
И в период охлаждения
Яв = . ($г1 — &в1) 1-е ^ V *в 1 ккси/м2. час. (785)
В. П
Здесь Ї — величина, характеризующая выражение, появляющееся в формулах противотока; в развернутом виде
1--^
І =------------------- 5-г-тгт - (786>
|
№. ■ е |
![]() -—-/і Ц I «'в /
-—-/і Ц I «'в /
П ж/7 - ч
После определения критериев ----------- и -------- значение [ най-
Дем по рис. 53. В большинстве случаев необходимо определить теплопередачу в конце регенератора. Для этого нужно подставлять соответствующие значения д. Тепловое напряжение поверх -
Ностн нагрева на входе газа (т. е. на выходе горячего шздуха) по уравнению (784) при Рх =0 равно
9вход = —— • {&Г1 —®в1> • !ккал/м2 • час. (787)
ТГ. П
Если температура подогретого воздуха &в2 известна, то <7ВХо* проше выразить следующим уравнением:
<7вход = ■ • (&Г1 — &вг) ккал/м2 • час. (788)
Тг. п
I
При определении теплового напряжения поверхности нагрева в воздушный период вместо тг<п необходимо подставлять продолжительность периода охлаждения твп. Тепловое напряжение поверхности нагрева ма стороне выхода газа (вход холодного воздуха) при
<7выход = «7вход • * ккал/м2 • аде. (789)
/
Если температура отходящего газа известна &г2, то <7ВЫход проще выразить следующим уравнением •
?вькоч = —— (&Г2 — &В1) ккал/м3 • час. (790)
Тг. п
В уравнениях (787) — (788) х представляет србой значение коэффициента теплопередачи периода на горячей стороне регене-
- ратора. Напротив, функция } и показательная функция в уравнении (789) дацыпо средним значениям х, т. е. х, р (см. числовой пример на стр. 473). В уравнении (790) х представляет собой коэффициент теплопередачи периода на холодной стороне регенератора.
Коэффициент теплопередачи периода х дан в уравнениях (583) и (755). Водяное число—это произведение веса на удельную теплоемкость или объема на его удельную теплоемкость. Если общий вес кирпича, участвующий в теплообмене в регенераторе, составляет О г кг, поверхность нагрева равна Т м2 и удельная теплоемкость с ккал/кг »"С, то водяное число, характеризующее 1 м2 поверхности нагрева,
= 0' с '11 ккал/м2 ■ °С. (791)
Г
Если 5 м — общая толщина кирпича, то
^ = ~‘С. Т. Ч, (792)
Где т) — степень использования кирпича (см. рис. 65 и числовой пример на стр. 468).
Текущее значение теплового напряжения поверхности нагрева дт и дв для регенератора определяется следующим образом:
|
Дв ==■ —-— • (дг — ав) ккал/м2 * час, (7,94) |
![]()
|
Тв. п |
![]() ДГ = —----- (&г — &в) ккал/м2 • час (793)
ДГ = —----- (&г — &в) ккал/м2 • час (793)
Где’ х —коэффициент теплопередачи периода по уравнению
|
&г и дв—средние температуры газа и воздуха, господствующие в рассматриваемой точке; тг. п и тв п —продолжительность периодов нагрева и охлаждения. По уравнению (775) текущее значение разности температур — $в (между газом и воздухом)
В Умножая это уравнение на величину —— или на —’ получим |
Уравнение (784) или соответственно (785).
В этих уравнениях Фп, йв1 °С — температура греющей и нагреваемой среды на входе, Рх м2 — поверхность нагрева, омываемая греющей средой до рассматриваемой точки. Так как Рх «а входе газа равна нулю, то тепловое напряжение поверхности нагрева на стороне входа газа или сооответственно на стороне выхода воздуха будет выражено формулой, в которой отсутству. ет множитель
|
|
Тепловое «напряжение поверхности нагрева на стороне отхо - „дящего газа вычисляется по формуле при подстановке Рх = Р.
Если же х— переменная величина, то в качестве значения и необходимо подставлять величину, справедливую в данной точке; напротив, функцию / нужно определять по среднему значению х. Это среднее значение, согласно сказанному на стр. 334— 335, дает правильные конечные температуры. Следовательно, необходимые для расчета разности конечных температур даны правильно по среднему значению х, а теплопередача определяется умножением этой разности температур на коэффициент теплопередачи х, справедливый в данном месте насадки регенератора.

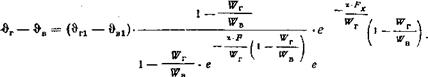
 Опубликовано в
Опубликовано в