Ниже излагаются те важные практические задачи, которые либо дают конечные решения простой формы, либо могут быть использованы в виде кривых и таблиц. При этом приводится лишь общий ход выводов и меньшее значение придается их по­следовательности. Те чцтатели, которые интересуются лишь прак­тическими решениями обсуждаемых задач теплопроводности и не придают значения знанию методов их получения, могут пропу­стить эту главу и пользоваться примерами расчетов, данными в разделе на стр. 438.

Математика дает различные решения* дифференциального уравнения (55)- Простейшим является случай, когда температу­ра не зависит от времени, т. е. наблюдается постоянный во време-

Д В

Ни тепловой поток. Тогда — =0 и уравнение (55) принимает вид

* дх2

Решение этого уравнения приводит к известному закону Фурье для стационарного теплового потока, выраженному уравнением (2а). Если, напротив, температурное поле изменяется во време­ни, то получаются значительно более сложные решения уравнения

(55) , а именно:

& =	= A + B	■ x + C - e~p x •	Eqx-	(60)
& =	=A + B■		■ cos (qx)	(6i)
& =	--A+B-	X + C ■ e~at''	• sinfax);	(62)
			-(«-*)*
& =	= A + B	T. С • x ----------- — • e	4a x T	(63)

V т * См. например, Н е 1 m h о 11 z, H., Vorlesungen ьber Theorie der Wдrme (Leipzig, Johann Ambr. Barth 1903). S. 36/46 u. 69/147.

2 ”]/" а т

Ъ = А + Вх + С-^[ • в“4[9] - сг^ (64)

Т)=0

Здесь величины Л, В, С, р, ^ — константы интегрирования, ко­торые могут быть равны нулю и являться положительными, от­рицательными или мнимыми величинами. Все эти примеры яв­ляются разновидностями решения уравнения (60), которое по­этому считается основным. Приведенные выше уравнения (60)— - (64) являются действительными решениями, в чем можно убе­диться при выводе частных формул и сравнении их, как это бы­ло описано при выводе уравнения (55). Теперь возникает вопрос: применимо ли к данной задаче какое-либо из этих решений или к ней можно применить сразу несколько решений? На этот вопрос необходимо ответить, так как соответственно с этим при реше­нии проверяют выполнение пространственных и временных ус­ловий (краевых, или граничных), после чего их соответствующим образом преобразовывают. Прежде всего необходимо убедиться в том, что каждое из решений применимо и дает правильные результаты. Поэтому не следует опасаться, что выбор неподходя­щего решения может привести к ошибке. Напротив, при по­пытке воспользоваться непригодным решением его неприемле­мость обнаруживается сама собой. Для пояснения этих положе­ний в дальнейшем необходимо рассмотреть дополнительно ма­тематические формулировки важнейших случаев.

Внезапное однократное изменение температуры поверхности бесконечно толстой стенки

Дана стенка бесконечной толщины с коэффициентом темпе-^ ратуропроводности а м2/час, начальна^мпература>,.котар©1Нтб::-# всюду одинакова и составляет^^йз^С^и поверхность которой при­обрела и сохраняет температуру ®Пов°С*. Тогда температура на расстоянии хм от поверхности через т часов составит

* = »по. + (»на, - *пов) • к (—°С. • (65)

2 У а т /

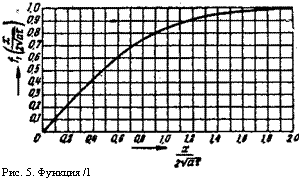
Функция /1 представляет собой «интеграл ошибок» Гаусса, зна­чение которого определяется по кривой, изображенной на рис. 5.

Тепловой поток, протекающий через плоскость, взятую парал-^ лельно поверхности на расстоянии хм от нее, спустя т часов со-

Ставит:

Х*

4 а х

(66)

Ккал/м*'Час.

У а • п - т

(67)

Рис. 5. Функция /1

Тепловой поток через поверхность через т часов а= М»няч-«пов)_ ККаЛ1м*-час. 1/а-я - т

Ьйг)

За первые т часов через поверхность пройдет полное количество тепла:

(68)

<2общ = 2: М»я, ч-»по,) |Д. ККал/М2.

Уа*

Вывод. Лрй решении задаемся краевыми условиями. Для т=0 и X — х »внутри стенки)

Ч ^ == ^нач

И для т = 0 и л: = 0 (на поверхности стенки)

® == ^пов•

Главной областью применения этих уравнений является изучение распро­странения тепла в грунте при постоянной температуре поверхности (каналы генераторного газа, регенераторы печи и т. д.).

На рис. 51 и 52 (см. стр. 308) даны графики функции е в зависимости от показателя степени (см. пример на стр. 438). Теперь попытаемся согласо­вать последовательно решения уравнений (60) — (64) с граничными усло­виями. По уравнению (60)

Для т — 0 должно быть

Ь = А +Вх + С - е-р' • е*х; Ъ = А + В - х + С • е*х-’

ПЕРЕДАЧА ТЕПЛА ТЕПЛОПРОВОДНОСТЬЮ

57

Т. е. с удалением от поверхности по оси х температура в начальный момент должна расти или уменьшаться по закону показательной функции (в зави­симости оттого, является q положительной или отрицательной величиной). Следовательно, уравнение (60) [10] применимо только для этого случая. Так как это не соответствует заданным начальным условиям, необходимо попы­таться применить следующее решение. По уравнению (61)

Ъ = А + В-х + С - (Taqt х. cos (<7 • х), если х *» 0, получаем

Т. е. температура поверхности должна во времени изменяться по экспоненте, что не соответствует заданным краевым условиям. Поэтому это уравнение также применить нельзя.

По уравнению (62) третье решение:

» = А + В • х + С • в-0«’т sin (q • *)

Или для начального момента времени (т — 0):

Ъ = А +£ • х - f С sin (q • х).

Это уравнение нужно рассмотреть более внимательно, так как для х = О будет Ф = А = const, и jto краевое условие выполнимо. По теории рядов Фурье такое чередование периодических функций sin или cos возможно и позволяет выразить любую заданную функцию. Следовательно, на поверх­ности (х = 0) должно быть:

Л = V

Но здесь возникает следующее затруднение. Раз толщина стенки беско­нечна, период полученной фун-кции будет бесконечно велик. Преодолевая это затруднение, Фурье создал свою теорию «интегралов Фурье», которая приводит к решениям уравнений (63) и (64) [11].

Решение равенства (63)

_ (*-*)»

8 = А + В ■ X + ~г-~ ■ е 4в * ;

, У х

Для т = 0 третий член уравнения будет равен нулю; Если же положить-. В = 0, то можно выполнить заданное краевое условие на поверхности:

Л

§Xss 0 = А = const.

Однако, если найдется точка, для которой х = q, опять возникает з^труд-

(4-х)*

Нение. Для этой точки выражение ---------------------------- для всех значении т равно нулю,

4а т

- (4-х)*

^ 4 ах

А выражение --------- —-------- для т = 0 будет равно бесконечности. Таким об-

V т

Разом, это решение также неприменимо.

Последнее решение дается уравнением (64)

2/ат

Ъ = А+В ■ x + C—^zr Г. в-ч* .dij.

V* J 11-0

X

Здесь необходимо принять во внимание, что' выражение--------------- ------ для х = 0

2 Vax

2 Г

И t * 0 будет равно нулю. Выражение—— le есть не что иное, как

V ТС J о

Х

«интеграл ошибок» Гаусса и для всех значений rj=——гможно найти в таб-

2 TOC o "1-5" h z Vax

Лицах (см. рис. 5). Для к = 0 он будет равен нулю и для г = оо единице. Для краевых условий х = 0, т = 0 из уравнения (64) получим:

Й = $0 = Л. (69)

Для х — х при Т = 0

•з-0 = A+B. x + C = bHi4. (70)

Так как по этому уравнению с увеличением х должна расти или убывать

Величина Фнач. что противоречит предположению, то В должно быть равно

Нулю. Следовательно,

^нач = ^ “Ь (70а)

Но, так как по уравнению (65) А = Ф0, то

С = $нач— «о. (71)

т. е. получается, что последнее решение удовлетворяет как начальному гра­ничному условию ( $№*=8Нач ), так и граничному условию на поверхно­сти для х = 0, '0' « 'О'о - Гак как никаких других краевых условий не постав­лено и не встретилось прерывности функции, как в предыдущем решении, то математическая формулировка для поставленной задачи найдена. Следова­тельно, по уравнениям (64), (69) и (71)

V7 Или сокращенно

» = 9» +(»на,-А) • f • в_Т‘‘ • dr> (72)

* J.

6 — $о + (^нач — »о) * /1 (------------- ^ °С. (72а)

2 Кет /

Отсюда с помощью графика (см. рис. 5) легко рассчитать температуру на любом расстоянии х м о г поверхности и для любого времени т. Количество тепла, поступающее внутрь или выходящее изнутри стенки через поверхность с постоянной температурой, рассчитывается по закону теплопроводности [см.

Уравнение (2)]. Сообразно с этим количество тепла, протекающее через стен­ку, составит

ДЬ

TOC o "1-5" h z О =2 X • — ккал/м1-час. (73)

/ дх

ДЬ

Следовательно, необходимо рассчитать ~ • Теперь получим *

2 У а т 2 У а т

Р d f - е~ч* .di) _ х2

<Э _т, , 0 Зі) “ 4а т 1

---- ; Є ч dr| =------------------------ • ----- =е •---- —:

дх J di] дх 2 У at

О

Или по уравнению (72))

Если это »выражение подставить в уравнение (73), то определим количество тепла, протекающее через сечение, расположенное иа расстоянии х м от по­верхности:

X»

4а х

В

0 = X (&нач — д0) .----- 1 ккал/м2 • час. (74)

V а • те • т

Как видно, количество тепла, протекающее через 1 лі2 сечения, сильно умень­шается по мере удаленйя от поверхности по оси х. Тепловой поток, прохо­дящей через поверхность (х = 0), определятся по уравнению (74):

(/ = X. -^нач......... ^1- ккал/мг-час. (75)

V а • те • т

Суммарное количество тепла, поступающее в стенку за период первых т ча­сов. составит

Р X • (&нач — »о) л / «

<?0бщ = I --------- —:------ л т ккал/м*

J ]/ а • те • т

О

Или после интегрирования

Ообщ = ккал/м%. (76)

Ка • *

Из-за бесконечно большого перепада температур в первый момент тепловой яоток согласно уравнению (75) для % 8=8 0 за бесконечно короткий промежу­ток времени будет бесконечно велик. Знак минус (Фо > Фнап} перед ф имеет лишь формальную причину *, которая »определяет направление потока, в то время как в численных значениях ничего не изменяется.

/ Из уравнения (70) следует, что с помощью примененного решения мож-

I Но также определить начальный температурный перепад в стенке. Следова-

I Тельно, начальные условия изменяются таким образом, что для х = 0 внутри ^ бесконечно толстой стенки температура увеличивается или уменьшается по

4 закону:

& = $нач ^Ьх °С.

Тогда для х ~ 0 и х = х по уравнению (64) при «интеграле ошибок», равном 1,

О == 9нац ^ Ьх — А В • х - С; (77)

Далее, для т = 0 и х = 0 по условию задачи ■0, = 'О, о, а следовательно, по ура]#нению (64)

Л = & о-

Подставляя это значение в уравнение (77), получим:

0 = ^нач £ Ь*Х.

Это уравнение справедливо для всех значений х, если

В-±Ь

X

И

Ь0 + С — 0цач

Или

С = &нач •

Поэтому для такого случая решение запишется ^

& = $0 ^ + (^нач — &о) Л. ( ~ ^ • (78)

гУах )

Соответственно, тепловой поток» через сечение определится выражением

X»

4а т

(79)

Д = X I ± Ь + (8нач — ®о) • —--- ------------- Г ккал/м*-час

[ Уа*т

И тепловой поток, протекающий через поверхность,

' = X • (± Ъ + —.............. ккал/м2’час. (80)

Vа • * • ^ /

Здесь К. Ъ ккал/м2 • час означает постоянный по времени первоначальный тепловой поток, который соответствует перепаду температур Ь (—— = Ь).

ИХ

Уравнение (80) показывает, что после очень длительного промежутка вре­мени снова устанавливается первоначальный температурный перепад Ь. При этом необходимо знать условие, когда применимо уравнение (80). Внешние

Г**

—величина отрицательная.

Причины, вызвавшие первоначальный перепад температуры, должны сущест­вовать также и после изменения температуры поверхности, т. е. в бесконеч­ности (или на второй поверхности стенки) должно быть отобрано такое же количество тепла А,, Ь, какое было необходимо затратить, чтобы вызвать температурный перепад Ь до наступления момента времен« х = О.

Внезапное однократное изменение температуры поверхности стенки толщиной 5 м

Приближенные формулы. Так как свойства стенки конечной толщины при кратковременных изменениях температуры те же, что и стенки бесконечной толщины, то выведенные выше формулы для бесконечно толстой стенки[12] применимы до известного момен­та, считая от начала нагревания, а также для стенок конечной толщины. Получается, что формулы приближенно применимы др тех пор, пока для первоначально холодных стенок, находящихся на открытом воздухе, выполняется условие

-^>0,6 2 Уаг

Или, пренебрегая начальным состоянием стенки,

2|/а т

Тогда температуры определяются по уравнению (65), а тепловой поток — по уравнениям (66) — (68)[13].

Называет уравнение (66), будет мало до тех пор, пока величина /|

Вывод. Очевидно, уравнения, полученные для бесконечно толстой стен­ки, должны быть применимы повсюду там, где изменение теплового потока, протекающего через вторую ограничивающую поверхность стенки, еще незна­чительно, т. е. повышение температуры на второй. поверхности еще мало, В этом случае изменение температурного поля во времени и пространстве в стенке конечной толщины можно определить довольно точно. Повышение температуры на второй поверхносии первоначально холодной стенки, как по-

Близка к единице. Этот случай, согласно рис. 5, справедлив для больших зна-

X X

Чений ----- иг - Величина------- щ; будет большой для толстой стенки и малого

2У а*т 2]/^а-т

Промежутка времени, - например для стенки толщиной 200 мм за 1 час. Какие же отклонения возникают в этой стенке по истечении длительного проме­жутка времени? Если коэффициент теплоотдачи от стенки к окружающей среде поддерживается всегда таким, что обусловленная им потеря тепла равна количеству тепла, проходящему через соответствующее сечение бес­конечно толстой стенки, то температурное поле конечной и соответствующей
части бесконечно толстой стенок было бы в течение длительного времени одинаковым. Необходимо предположить, что температура окружающей среды соответствует начальной температуре стенки Онач. Тогда теплоотдача от по­верхности, нагретой до О0, к окружающей среде составит

Д =<х(&— &нач) ккал/м1 час.

Этот тепловой поток должен быть равен тепловому потоку, проходящему через сечение, взятое в бесконечно толстой стенке параллельно ее наружной поверхности и отстоящее от нее на расстоянии 5 м. Согласно уравнению (74), он равен

X*

4а х

Е

0= X ($нач — $о) *----- ".......... " ккал/м* час.

/ а • л • т

Приравнивая правые части вышеприведенных уравнений, нахбдим коэффи­циент теплоотдачи, необходимый для установления желательного теплового потока:

X*

X (йНяч — 9ц) * В

А = —---■•■■ - ------------------ ккал/м*-час-°С. (81)

У^а * гс • т ($ &нач)

Так как распределение температур в стенке конечной толщины и в беско­нечно толстой стенке должно быть одинаковым, то О определяется из урав­нения (65). Если начальная температура стенки 'б, Нач= 0, а О определяют по уравнению (65), то искомый коэффициент теплоотдачи

SHAPE \* MERGEFORMAT

І» 4 а х

X • е

Ккал/м2 * час -°С. '(82)

Я2

Зависимость коэффициента теплоотдачи от ---------------- , определяемая по этой

4а**

Формуле, дана на рис. 6. Рисунок показывает, что большинство значений коэффициента теплоотдачи, часто встречающихся на практике, находится в2

В области значений —-------- , составляющих от 0,4 до 1,5. Величина 1,5 для

4а* т

В2 5

*---- соответствует 1,2 значения ------------- ------- , данного на рис. 5. Согласно

^ 2Уа-х

Рис. 5 для этого значения функция /1 I-------------- щ.) уже равна 0,91 и, следова-

2Va-,

Тельно, близка к единице. Так как с дальнейшим увеличением ——истенка

2 Уа-х

Конечной толщины все более приближается по своим свойствам к бесконечно7 толстой стенке, то можно сделать вывод, что формулы приближенно дей-

В2

Ствительны для стенки конечной толщины до тех пор, пока ----------------------- > 0,4

4а - х

Или соответственно -------- > ОД Ниже этого значения в стенке конечной

2 V а • т

Толщины устанавливается стационарное состояние, при котором уравнение (65) недействительно. Необходимо еще раз подчеркнуть, что эти выводы действительны лишь в там случае, когда начальная температура стенки мала и приблизительно совпадает с постоянной в течение длительного времени температурой окружающей среды. Следовательно, формулы будут применимы главным образом для случая первоначально холодной стенки, находящейся на открытом' воздухе.

Рис. 6. Изменение коэффициента теплоотдачи на второй поверхности стенки

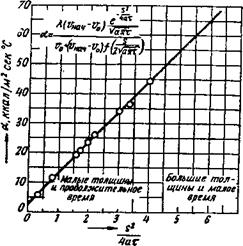
Точные формулы. Американские ученые Е - Д. Вильямсон и Л. X. Адамс [14] рассчитали изменение температуры в середине пластины, шара, цилиндра и квадратного бруса в случае вне­запного изменения температуры поверхности. Если первоначаль­но во всем теле господствует равномерная температура Ь, ач и вдруг вся поверхность приобретает температуру ф0, сохраняя ее до конца, то температура в середине тела

» = %+ »о)/.(-^•)вс, ' (83)

Где 5 — толщина стенки, диаметр шара или цилиндра или длина стороны поперечного сечения бруса, м. Функция /*2 определяется по кривым, изображенным на рис, 7 (см. числовой пример на стр. 440).

Вывод. Ниже будут рассмотрены только процессы в стенке толщиной $л(с бесконечно большой поверхностью; это ограничивает задачу лишь одной координатой, т. е. указанной толщиной стенки.

Начало координат располагаем в средней плоскости стенки, так что по-

В 5

Верхности характеризуются координатами + - т - и — . Начальная тем-

» * ^

Лература стенки может быть выражена любой заданной функцией расстоя-

Рис. 7. Изменение температуры в центре различ­ных тел при внезапном изменении температуры поверхности: I — пластина; 2 — брус квадратного сечения бесконечной длины; 3 — цилиндр бесконечной длины; 4 — куб; 5 — цилиндр, высота которого равна диаметру; 6 — шар

«ия х от средней плоскости. Следовательно, начальное распределение тем­ператур можно представить следующим образом

»=/(*)•

Температура обеих поверхностей должна быть постоянной величиной, рав­ной Фо °С.

Таким же методом, что и в задаче, рассмотренной ранее, находим, что на этот раз уравнение (61)

_ аа% т

О = А + Вх + С-е соэ^-х) (84)

Пригодно, так как начальные условия выполняются. Согласно краевым усло­виям, температура обеих поверхностей должна быть всегда постоянной; еле*

»0 = Л+В. - у+С. є-“*’'cos (85)

(86)

S И для х = — —

> = А~в' 1~ + с'в 04*г' cos(9'l')*

S S

Так как cos(—<7—) равен cos(-f<7~).

Из уравнений (85) и (86) црежде всего следует, что температура Фо

S

Лишь тогда постоянна, т. е. независима от т» когда cos q тш^т = 0. Это ра­венство соблюдается в том случае, если

7Г Зтс (2п — 1) те

TOC o "1-5" h z Я = —, ---------- , , (87)

S S S

Т. е. для бесконечно многих, но вполне определенных значений q. На осно­вании этого определяем температуры обеих поверхностей стенки

Ъ0 = А + В-^~ (88)

2

2 *

Следовательно,

А+В— = А-В —

2 2

Это уравнение может быть справедливо только при В = 0. Тогда из уравнения (88) следует, что

А = Ъ 0. (90)

Основываясь на этом, из уравнений (84), (87), (88) и (90) получим

(2п — 1)атс*а х

~~ х* (2 п — 1) 7хг д:

Ъ = Ъ0 + Сп-е * соз ------ ^------- . (91)

Это уравнение, как мы только что видели, удовлетворяет условиям на по­верхности для любого целого и положительного значения, т. е. для л = 1,

2, 3, 4..... оо [(2л—П —всегда нечетное число!].

Если примем, например, п = 1, то получим

J* те • X

$ = 4" С • є • cos"

S

И для начальных условий, т. е. в случае т = 0,

&о + С • cos-^(92)

5 А. Шак

Очевидно, по это^у уравнению нельзя определить началькую температуру стенки, которая должна быть всегда равна ОнаНо, как показывает теория рядов Фурье, каждая функция, в том числе и постоянная величина, может быть представлена суммой выражений типа уравнения (92), т. е.

/1=00

TOC o "1-5" h z / (*) = *н., = »0 + 2 • С„ • cos (2аТЛ>?*. (93)

П = 1

При этом по теории рядов Фурье постоянная Сп равна:

+S

(2л — 1) тс л: в л

Cos ■ • dx (Онач — 1

S

Сп — * --------------------------------------------------------------- . (94)

С. (2n — l)it* j

I «cos*---------------- dx

—5

После интегрирования получаем

°п = (2л — 1) я (®вач “ &о) ’ (95)

Где знак плюс соответствует всем нечетным значениям п. Тогда уравнение (93) примет вид

П Г 4 тс х 4 Зтгх

^нач — “Ь (^нач — ®о) * cos 0 cos ~f"

I Те S Зтс S

4 5те х 4 7пх 1

4-------- cos------- —------- - cos--------- Н---- ... . ^ (96)

Т 5тс s 7тс s J

Теперь мож1но проверить, действительно ли с помощью найденного ряда Фурье можно выразить постоянную начальную температуру 0,а. В самом деле, уравнение (96), например, для х = ±0 (середина стенки) преобразуется следующим образом:

Онач = $0 4- ($нач ^о) * ^ ^ ^ ^ + • • • J»

^нач = ^нач*

Те

Так как выражение в скобках равно.

Аналогично уразнение (96) было бы справедливым для любого другого

5

Значения х, которое лежит между 0 и ± -j-. С другой стороны, правая часть

S

Уравнения (96) для х = ± (поверхность стенки) принимает значение Фо*

Что соответствует поставленной задаче.

Подставляя найденное значение С п в уравнение (91), получим

А *а

Ft = Oq - f* (Онач — 00) fe • COS

Те S

9те*а х 25к2а г

Или сокращенно

(2п — 1 )2а кат

» = »о + (»на[15]~--- 2n~^~l------ C°S (2П!)ПХ ■ <97a>

П = 1

Это и будет решением поставленной задачи. Оно дает возможность опреде­лить температуру б любой точке плиты для любого момента. Если бы начало координат находилось не в середине стенки, а на ее поверхности, то получи­лось бы совершенно аналогичное решение, но с применением синуса вместо косинуса.

Стенки толщиной в м в теплопередающей среде постоянной

Температуры

В предыдущей задаче рассматривалось собственно изменение температуры самой поверхности*. Теперь необходимо решить за^ дачу, когда пластина толщиной в м омывается с обеих сторон га­зом (или жидкостью), имеющим постоянную температуру &г °С, причем коэффициент теплоотдачи равен а ккал/м2-час-°С[16].

Равномерная начальная температура пластины равна &нач °С. Тогда температуру поверхности пластины через т часов можно определить по уравнению

TOC o "1-5" h z »0 = »г + (»„а,-»г)/з(-^, ^)°С’ <98>

А температуру средней плоскости

»ср=»г + (»нач-»г)-/4(-^, -^у-)°С - (99)

Количество тепла, полученное стенкой за первые т часов, соста­вит

<2 = в • с • т (&нач — аг) /5 ккал/м2. (100)

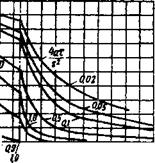
Функции и, /ч, были рассчитаны Г. Гребером[17] и могут быть взяты из графиков, изображенных на рис. 8, 9, 10 (см. числовой пример на стр. 442).

Вывод. Температура поверхности пластины Фо, 'Правда, не постоян­на, как в предыдущей задаче, но определяется простым условием. Количе­ство передаваемого тепла

Д = а (йг — $0) ккал/м*-час (101)

Должно быть равно количеству тепла, проходящему через вгнешний слой пластины,

/ д

(102)

Л = X • I------- 1 ккал/мг-час

дх )Хгш .

КЯИ№ КЯІ10№ ЕВ1ШЯ КН1М Ю№Б

В 00 т 0.103 О! V 10 6,0 т НО цо <Ю Ж

Рис. 8. Изменение температуры поверхности стенки тол - шиной в м при теплообмене с окружающей средой

Со* ШЦ! уматШго То ю. о но чо 1 %

Следовательно,

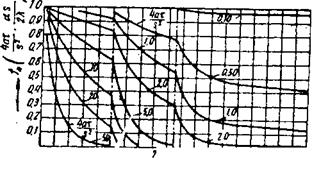
Рис. 9. Изменение температуры в средней плоскости стенки толщиной 5 м при теплообмене с окружающей средой

/

А(»г-»,) = ^К-

При решении »предыдущей задачи оказалось, что косинусоидальная функ­ция пригодна для описания симметричного распределения температуры, зна­чения которой равны как в положительном, так и в отрицательном направ­лениях оси х. Поэтому применим опять уравнение (61):

» хс А + В ■ х + С • е~ “«* * • сое (я • х). (104)

Коэффициент В снова должен быть равным нулю, так как он нё соответствует

Симметричному распределению температуры. Граничные условия на йоверх-

0 (МП (108(1103 05 07 й9101О 6.0 ----- •- *£ 2	Т /до
Рис. 10. Тепло, воспринятое или отданное стенкой тол­щиной « м при теплообмене с окружающей средой

Ности не относятся, как прежде, непосредственно к О, а имеют зиачение лишь д &

Для - г - • В соответствии с этим, по уравнению (104) ох

(105)

Далее для х = ± —согласно уравнению (104),

(106)

8 = = А + С • е~ аг'х • сої

Из уравнений (103а) и (105) следует, что

— С ■ е~а«г х • <7 • біп =

(107)

=тЬ“л-с-е"ав’х-С05(9 т)]-

Это уравнение справедливо для всех значений % и 5 ПРИ условии, если

А = 8Г (108)

И

*

(109)

Уравнение (109) показывает, что <7 не является, как раньше, кратным Л, а представляет собой число, которое необходимо определить из уравнения (109). Следовательно, получается, что уравнение (109) справедливо для бесконечного ряда вполне определенных значений <71, <72, .... Я л- На основа­нии этого, как и в прошлой задаче, перейдем сразу к сумме ряда и из урав­нений (104) и (108) получим следующее выражение:

%П = со _ 2

$ =г $г + ^ Сп • в соз (<7Л • х). (110)

П ~ 1

. 5

Для условий х = 0, х = ± это урав(нение преобразуется следующим об­разом:

П =» ОО

$ 5= $г * соз = ^нач* (111)

П = 1

Постоянную Сп, согласно теории рядов Фурье, можно определить из следую­щего уравнения:

Соб (дп • х) сіх

Сп = (^г—^нач)- (И2)

+ —

2

I с/»* (дп ■ X) <1х

2

Здесь значения являются корнями уравнения (109) и определяются из него путем подбора или графическим способом.

Дальнейшее решение уравнения (110) с помощью уравнений (109) и (112) показывает, что распределение температуры в пластине зависит, как и в

TOC o "1-5" h z А • т х

Уравнении (97а), от величин и — или, если подставить расстояние до

Б2 э

В 4ах 2х

Поверхности *— , от —- и —; кроме того, в данном случае влияет еща

2 в* я

А в

И величина -£т - .

2 А.

Следовательно, получим уравнение

(

4а х 2х а • в

~7"* «‘•"гГ)- (113)

X

Г. Гребер решил уравнение (ИЗ), для определенных значений — и на

Основании этого составил таблицы. и кривые (— =1—поверхность и

5

2х 2х

■— =0 — средняя плоскость). Для указанного постоянного аначения —

Б 5

Уравнение (ИЗ) преобразовано следующим образом

& = »г + (»на..-М/з (ПЗа>

2х

Изменение температуры поверхности (----------- = 1) /з и средней плоскости

Б

2х

— = 0) /4 было вычислено Г. Гребером [18]; результаты вычисления графи - в

Чески изображены на рис. 8 и 9.

Как и в уравнении (73), тепло, воспринятое или отданное стенкой, можно определить, если известно температурное поле.

Исходя из этого условия получим выражение

(

4а т а • э

—) мм/м*. (114)

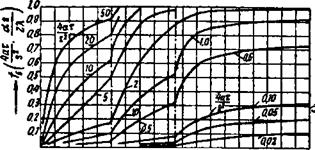
Функция /5 также рассчитана Г. Гребером (рис. 10).

Периодическое изменение температур обеих поверхностей стенки толщиной 5 м

В прежних задачах были рассмотрены лишь случаи с условием постоянства температуры поверхности или температуры окружа­ющей среды.

Теперь рассмотрим стенку, температура обоих поверхностей которой должна периодически изменяться по закону

^ = дср + Ддмакс. С05-^1-оС. (115)

Тпер

Тогда изменение температуры в средней плоскости стенки сос­тавит:

М == Д&мзкс/в °С - (116)

Функция /6 была рассчитана Гребером; результаты этого расчета графически изображены на рис. И (то = тПер).

Коэффициент использования аккумулирующей способности стенки г] выражается отношением действительно усвоенного теп­
ла к количеству тепла, которое может быть усвоено стенкой при бесконечно высокой ее теплопроводности. В соответствии с этим

(117)

Функция /7 также была вычислена Г. Гребером (см. рис. 11). Ко­личество тепла, воспринимаемое единицей поверхности стенки за

1- -			Л
Г	/-
Я	А	7
		-2
	У
Г , /#
1 И ’ІІ				,
У

0 12 3 4

5 6 4 а Т0

7 8 9 10 П

I* ] т

КЬ Г Н'

Рис. 11. Колебание температуры середины кирпича относительно колебания температуры поверхности, равной 1 и коэффициент использования кирпича ц: / — йбэффицйёнт использования т4; ^ — колебание тем­пературы /е^4а—‘ | В центре

Половину периода час. при равной продолжительности пе­

Риодов нагревания и охлаждения), равно

(118)

Q = <2макс • V ккал/м*

(119)

Смаке

: С • 5 • 7 • Ммакс ккал/мг.

Известно, ЧТО Яыйкс — это~такое количество тепла, которое быЛо бы усвоено кладкой при ее абсолютной теплопроводности, так как в этом случае температурное колебание внутри стенки имело бы ту Жё величину, что и на поверхности.

Где

В вышеуказанных уравнениях:

&0 — переменная температура поверхности, °С;

^ср—средняя температура поверхности за период, °С: Аммане — наибольшее положительное или отрицательное откло­нение температуры от &ср за период, следовательно, амплитуда колебания, °С; тпеР—длительность всего периода (в регенераторах: период газа + период воздуха), час/,

* — длительность процесса t начала перибда, час.; s — толщина стенки, м; .

А — коэффициент температуропроводности стенки, м2/час; с —удельная теплоемкость материала стенки, ккал/кг*°С; Т —удельный вес материала стенки, кг/м$.

Вывод. Принимаем начало координат снова в средней плоскости стенки. Температуры обеих поверхностей могут изменяться прежде всего во време­ни по закону:

#о = /00-

Так как в этой задаче речь идет о симметричном распределении темпера­туры, то можно опять применить уравнение (61)

& = А + В • х + С • qt° х • cos (g • х). (120)

S

Теперь ДЛЯ X = + —ДОЛЖНО быть

» = /(х)^л+в-^-+С е-,,вх- с“ (*•"§") (121)

S

И ДЛЯ X = — —

Ь = f (z) = А — В -+ С - е~й%ах »cos (121а)

Эти уравнения одновременно справедливы лишь в том случае, если В = 0. Тогда

F{x) = A + С ■ е-*’ах • cos^ (122)

Для упрощения необходимо с самого йачаЛа представить / как периодичес­кую функцию

/ (т)= ^ср Ч" А ^макс * cos • (123)

Тпер

Приравняв правые части уравнений (122) и (123). получим

В этом уравнении постоянные величины одной части уравнения должны быть равны постоянным величинам другой части уравнения, следорательно,

TOC o "1-5" h z С • cos ^<7 2 | ~ А ^макс» (125)

Тогда

Е~ g*aT = C0S 27t ~. (126)

Тпер

Лишь на первый взгляд кажется, что решить это уравнение невозможно, одна­ко необходимо принять во внимание соотношение:

El * = cos Ф + i • sin<P, (127)

Где i 5=]/—1. Следовательно, от функции числа е можно перейти к инте­ресующей нас функции cos, если q2 примем мйимым, т. е.

<?2 = Ф2, , (128)

Где р— действительная величина. Тогда из уравнения (127) получим

• 2 7С X

Е— ip*a т cos ^р2а т) I sjn __ cos

Тпер

Ак как действительные части должны быть равны, то п i J Z

2тгт - i,

Cos (p2a т) = cos------------------------------------------ - f у L

Или

2тгт ґ 2п

(129)

Р2аг=------------- , р=± 1/ . ^

^пер V а тпср

Тогда по уравнению (128)

Я уравнение (120) преобразуется в выражений,».і с? С

_ /2 *т 6Й * С Ус

8-,„ + с. Г

В ходе решения следует принять во внимание, что

УТ=±4-(/2"+<УТ),

В результате приходим к более сложному решению, которое содержит в ка-

TOC o "1-5" h z а • тпер X

Честве переменных величин----------- — и —

S S

(130)

Данное решение в-противоположность прежним рассматриваемым зада­чам приводит к конечному выражению. Причина в том, что не было постав­лено никаких требований для начального распределения температуры; более

Того, было принято, что периодическое нагревание поверхностей продолжает­ся уже длительное время. При этом стационарное состояние устанавливает­ся в такой форме, что температура в каждой точке внутри стенки по истече­нии периода всегда снова принимает прежнее значение. Если бы было постав­лено условие, что в начале господствует некоторое распределение температу­ры, то для приведения температуры к «установившемуся состоянию» снова было бы дано выражение суммы. Для других случаев также было бы дано ре­шение в виде рядов вместо простых синусоидальных или косинусоидальных изменений температуры во времени. Для различных простых законов измене­ния температуры поверхности стенки Г. Гребер рассчитал тепловой поток, проходящий через эту поверхность. Максимум затухающего колебания тем­пературы, происходящего в кладке, определяется уравнением

TOC o "1-5" h z. Л а ( , / 4а тпер? х

(131)

А® — Д^макс/в! ^2 > а )’

Где 5 — толщина пластины, м

Аммане — наибольшее отклонение температуры поверхности от средней температуры поверхности, °С.

/4итпер 2х „ /

Функция Ы—^------- » — Для средней плоскости стенки I — = 0 1 бе­

Рется из рис. П. Температура середины между поверхностью и средней пло - I Л

Скостью I — = 0,51 лишь незначительно отличается от температуры сред-

(Т~0, )

Ней ПЛОСКОСТИ.

Знание количества тепла, аккумулированного или отданного за полови­ну периода, является более важным, чем знание распределения температуры Как и раньше, его можно рассчитать, если известен перепад температуры /д 0

I“т— I 5 на поверхности [см. уравнение (73)]; а именно, количество

дх ' х = ± —

Тепла, приходящееся на поверхность за время с/х» составляет

А &

= X —-— й т ккал/м2. дх

Количество тепла, аккумулированное 1 м2 поверхности стенки за половину периода, равно

Тпер

2

X т ккал/ч».

0

Аа

( 4а тпер Л и )

Решая это уравнение, предварительно определивиз уравнения (130), полу« чим

С ^ Смаке /71 о ) » (132)

Где <3 — такое количество тепла, которое было бы аккумулировано стенкой, если бы ее коэффициент теплопроводности был бесконечно высок; следова­тельно, температурные колебания по всей толщине стенки были бы такими же, как и на поверхности. Так как ДЙМакс СС является наибольшим отклоне­нием температуры поверхности от среднего значения, то 2А0макс °С является

Полным отклонением, а соответствующее ему аккумулирование тепла в клад­ке с бесконечной теплопроводностью составит

Фмакс = 2 • $ • Г • У • А ^мякс* (133)

Чтобы определить Семаке* приходящееся на 1 л3 поверхности Стейки, не­обходимо уравнение (133) разделить на 2, так как о*ю бтноситСя к 1 л2 обеих поверхностей стенки, т. е. к 2 м1 поверхности нагрева. Следовательно, макси­мальное количество тепла, получаемое 1 л2, составив

Рмакс == 5 • г • 7 • Аммане ккал1м^. (133а)

<2

Отношение т------- представляет собой степень использования аккумулирующей

Умакг

Способности кладки. Руководствуясь общепринятым обозначением коэффициен­та полезного действия, лучше всего степень использования обозначить че­рез т), так что согласно уравнению (132)

/ 4а * ,тпер *

Ч ^

И количество переданного тепла

Я = <2име • ч ккал/м*. (132а)

• ^ПСР

Коэффициент я зависит бт значения^--------------- —и подчинявшей закону, по кото­

Рому происходит колебание температуры. Для случая синусоидальной или косинусоидальной формы колебания значения г графически выражены на рис. 11.

Периодическое изменение температуры поверхности бесконечно толстой стенки

Уравнение (115) описывает случай, когда температура поверх-' ности изменяется по закону косинусоидальных колебаний. При­нятые при этом буквенные обозначения сохраняются и в дальней­ших рассуждениях.

Скорость распространения температурного колебания (напри­мер, максимальной температуры периода) в бесконечно толстой стенке определяется уравнением

TOC o "1-5" h z а) = 21/ -—■■■ м/час. (134)

У *пер

Интервал между двумя следующими один за другим максималь­ными значениями температуры (длина волны) равен

Х1 — х2 = 2 • а • тпер м. (135)

Количество тепла, получаемое или отдаваемое 1 м2 поверхности бесконечно толстой стенки за половину периода,

Я - 0,80 • А9-макс • • с. ? тпер ккал/м*. (136)

Среднее часовое количество тепла, воспринимаемое или отдавае­
мое за половину периода (тепловая напряженность поверхности нагрева), равно

Яср = 1.60 • Л&Макс 1/"-— У ккал/м2час. (137)

У тпер

Отношение тем! пературных колебаний, взятых на поверхности (Д'&макс) и на расстоянии х м от поверхности (А$), выражается уравнением

•V-

Лер

А»

А&»19Кс

Эти уравнения справедливы для стенок конечной толщины и бу­дут давать тем более точные результаты, чем больше величина

Я л/ —-—. (Если рассматривается стенка, обогреваемая с У я-тпер

Обеих Сторон, то о точности судят по значению выражения

—-—.) Практически достаточная точность достигается

Я[19]Хпер ______

При значении в 1/ —-—>2,5.

*' а-хпер

Согласно уравнению (134) скорость распространения темпе­ратурного колебания растет пропорционально коэффициенту тем­пературопроводности а. С другой стороны, количество восприни­маемого тепла по уравнению (136)зависит не от коэффициента температуропроводности, а от обычного коэффициента теплопро­водности, удельной теплоемкости и удельного веса.

Скорость распространения температурного колебания по урав­нению (134) будет тем больше, чем короче продолжительность колебания, т. е. чем внезапнее изменение температуры во време­ни. Уравнение (136) для бесконечно короткой длительности ко­лебания температуры поверхности дает бесконечно высокую скорость распространения, что не соответствует действительно­сти. В этом заключается принципиальный недостаток основного дифференциального уравнения. Уравнение не соответствует дей­ствительности (на что обратил внимание Ф. Рихарц*), если на­ступает сверхвнезапное изменение температуры. Поэтому реше­ния этого уравнения также не применимы для первых моментов рассмотренного случая внезапного изменения температуры в бесконечно толстой стенке (см. числовой пример на етр. 443).

= е

(138)

Вывод. Для бесконечно толстой стенки, колебания температуры поверхно­сти которой подчиняются уравнению (115), применимы те? ке рассуждения, что и для стенки ТОЛЩИНОЙ 5 м. Они приводят к уравнению

-к- 1 а тп

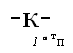
Ft = &Ср - f - Д$макс • е

2ітт. / к 1

'V с ,139)

Тпер V а TnepJ

Как следует из уравнения (115), &ср + Аймаке является наивысшеи достигну­той температурой (например, для т = тПер) и &ср—Аймаке наименьшей тем­пературой поверхности (для х— ), следовательно, полное колебание тем­пературы за один период равно 2ДФ Макс °С. Длина волны определяется по уравнению (139) следующим образом. Волна, как известно, представляет собой расстояние между двумя одинаковыми состояниями движения, например* между двумя точками, где колебание температуры достигает положительного максимума. Максимум наступает каждый раз, когда член уравнения cos = *= +1. Первый раз этот максимум. появляется в уравнении (139), если

SHAPE \* MERGEFORMAT

• |/ —----------------- 0. Г а * тпер -**• 1/ —1- = 2«. у а Тпе

2тст --- — *1

‘пер Т и * тпер

Второй раз, когда (cos 0=1)

2гт

Тпер У а тпер

,-*)• [/ —— =2*. Г а тпер

Расстояние X]—х2 равно искомой длине волны. Вычитая из последнего урав­нения предыдущее, получаем ^

(*i-

Ер

Искомая длина волны определяется уравнением

— 2 тс • а • Тпер м. (140)

Скорость распространения волны, как известно, равна отношению длины вол­ны к продолжительности периода колебания. Так как продолжительность пери­ода колебания, согласно уравнению (115), равнахпер час., то скорость распро­странения волны в теле бесконечно больших размеров

М/час. (141)

Аа

Определив из уравнения (139) значение выражения X “Т" ДЛЯ * = 0, находим

Ох

Количество тепла, протекающее за половину периода через поверхность внутрь бесконечно большого тела:

■ х*

<? = 0,80 • Д9макс • V* ■ с • 1 - Ухпер ккая/м*. (142)

Чтобы найти среднечасовое количество тепла, необходимо уравнение (142) разделить на продолжительность половины периода, следовательно,

V тпер

<7ср — 1 »60 • Д&макс 1/ ~г —— ккал/м2*час. (143)

Тепловой поток будет тем больше, чем больше коэффициент теплопроводности, и тем меньше, чем больше продолжительность периода колебания тПер - Для точки, удаленной от поверхности на х м, полное максимальное изменение тем­пературы за один период по уравнению (139) определится из выражения

2Д» = 2Д8ма1(с • е пер.

Поэтому отношение температурных колебаний на поверхности и на расстоя­нии хм от поверхности составит

-жу —

Г ° тпер

ДО Аймаке

Критерий Фурье

В гидродинамике и теории подобия появились связанные одна с другой группы переменных, которые совместно образуют без­размерные «критерии», например известное число Рейнольдса (см - стр. 89). Критерии сильно облегчают исследование про­цессов; особенно полезно применять их при анализе работ, где приняты разные'системы измерения, например система СйБ, тех­ническая система (кг, м, час) или английская техническая систе­ма измерения.

Сейчас, как видцо из приведенных выше решений общего ура^ внения теплопроводности Фурье, появляются все новые и новые

Безразмерные группы переменных, подобно выражению —

В[20]

Здесь 5 будет полной толщиной стенки. Если принять, что 5 — половина толщины стецки, то выражение запишется

Р°— (144)

Этот критерий получил название критерия Фурье (^о).

В интеграл ошибок Гаусса также введен критерий /ч) в виде

У/" А).

Без применения какого-либо уравнения, путем одного лишь

Рассмотрения критерия —, можно получить ряд важных выво-

В2

Дов для практических задач. Если вместо коэффициента темпе­ратуропроводности подставить его составные части, то уравнение

(144) преобразуется следующим образом:

Ро= (144а)

С- ( ■£*

Из Зтого уравнения, например, следует, что для определен­ного нестационарного процесса передачи тепла теплопроводно­стью критерий /о остается постоянным, если коэффициент тепло­проводности удвоить, а длительность нагрева уменьшить в два раза. Следовательно, нагревание или охлаждение, т. е. по^е тем­ператур, также останется неизменным. Или, выражаясь иначе, продолжительность нагревания обратно пропорциональна коэф­фициенту теплопроводности. Далее из уравнения (144) следует, что при увеличении толщины слоя вдвое необходимое время на­гревания возрастает в 4 раза, т. е. продолжительность нагрева прямо пропорциональна квадрату толщины слоя.

Пример. Один прокатчик предложил проталкивать слитки через печь не одним слоем, как обычно, а двойным. По его мне­нию, время выдержки слитков в печи при этом удвоится, что дол­жно улучшить прогрев. Из уравнения (144) следует, что для оди­накового нагревания при двойной тЪлщине стенки необходимое время нагревания должно увеличиться в 4 раза. Следовательно, предложение неприемлемо.

Критерий Фурье в качестве необходимого и достаточного ус­ловия для сравнения двух температурных полей занимает среди других безразмерных критериев особое место. Как объясняется на стр. 114, сравнение критериев подобия является необходимым, - но недостаточным условием для подобия потоков. Так, например, при числах Рейнольдса 3000 или 5000 движение может быть тур­булентным или ламинарным, а также можно говорить и о не - стабилизированном потоке (см. стр. 90). Критерий <£урье не име­ет подобных неопределенностей. Поэтому область его применения необходимо расширить*.

В. Приближенный метод Е. Шмидта

Вышеприведенные строго обоснованные решения, к сожале­нию, дают формулы, практически применимые лишь в ограничен­ном количестве случаев, или же требуют большой работы по со­ставлению кривых и таблиц, которых пока цет. Это особенно справедливо для тех «случаев, когда при периодическом изменении температуры поверхности оказывает влияние еще и начальное распределение температуры или, наоборот, когда температура поверхности постоянна, а начальное распределение ее в теле не подчиняется прямолинейной зависимости. До сих пор существуют

(103 а), если после небольших преобразований іввеоти б него критерий Био и выразить перепад температур:

Распределение температуры по сечению стенки в этом случае будет харак­теризоваться значительным перепадом между температурами на ее оси и по­верхности. Следовательно, процесс теплообмена будет определяться главным образом условиями распространения тепла внутри твердого тела (в данном случае пластины), а не условиями теплоотдачи на ее поверхности. Практи­чески условие

Ві — со ■

Можно заменить условием

Ві> 100.

Наоборот, при ВІ-+- 0 (практически В і < іОД) распределение температуры в твердом теле отличается большой равномерностью. В этом случае процесс теплопроводности будет определяться условиями теплообмена, происходящего на поверхности стенки.

Б) Более подробное изложение вопросов теплопроводности можно найти в следующих работах на русском языке:

.Лыков А. В., Теория теплопроводности, ПИТТЛ, 1952;

Лыко-в А. В., Теплопроводность нестационарных процессов, 1948;

В ей ник. А. И., Приближенный расчет процессов теплопроводности, ГЭИ, .1959;

Кондратьев. Г. М., Регулярный тепловой режим, ГИТТЛ, 1962;

Михееїв М. А., Основы теплопередачи, ГЭИ, 1956;

III о р и н С. Н., Теплопередача, ГИЛСиА, 1952*

Чубно^ский А. Ф., Теплообмен в дисперсных средах, ГИТТЛ, 1954;

Гухман А. А., Физические основы теплопередачи, ГЭИ, 1934;

,К у т а т е л а д з е С. С., Основы теории теплообмена, Машгиз, 1957;

Иванцов Г. П., На/грев металлов, 1948;

Эккерт Э. Р., Введение в теорию тепло - и массообмена, ГЭИ, 1957;

Б ос фо рт Р. Ч. Л., Проценты теплового переноса, ГИТТД, 1957;

Греб ер Г., Эр к С. и Григулль У., Основы учения о теплообмене, ИЛ, 1958;

Шнейдер П., Инженерные проблемы теплопроводности, ИЛ, 1960.

■ Кроме того, см. список рекомендуемой литературы на стр. 85. (Прим. ред.)

6 А. Шак

Решения лишь для некоторых видов распределения температуры на поверхности, причем они не совпадают по точности с данными практических наблюдений. Для целого ряда случаев вообще нельзя найти решения дифференциального уравнения. Поэтому в таких случаях рекомендуется применять указанный прибли­женный метод Е. Шмидта [21], который основан на решении диф­ференциального уравнения. Если в уравнение теплопроводности (55) [22] вместо бесконечно малых изменений дх, д& и т. д. под­ставить какие-то конечные значения Ах, ДО и т. д. то уравнение (55) можно преобразовать в выражение

Дх2

Дт

(145)

Здесь означает повышение температуры О0 за время

Дт час на постоянном расстоянии хм от поверхности. Для приме­нения уравнения (145) рассматриваемую стенку необходимо мыс­ленно разделить на определенное число слоев толщиной Ах за­данное общее время прогревания также делят на определенное число промежутков времени продолжительностью Ат. Тогда из уравнения (145) получим <

?)°С. (146)

Здесь п — номер соответствующего промежутка времени и т— номер слоя. Промежуток времени Ат час выбирается не произ­вольно, а в связи с выбранной толщиной слоя Д* м по уравнению

(147)

А (А X)2 Дт = -—час.

2 а

Необходимо усвоить большое количество индексов в уравне-

Нии (146) и применять иіх, зная какая температура подразумева­ется.

Л дт, (т+ 1)<л* —означает, например, температуру в рассмат­

Риваемой пластине, спустя пАх час. после начала процесса на рас­стоянии (т+1) Ах м от поверхности.

^(«+1)дт тьх —означает температуру на расстоянии тАх хм от поверхности, спустя (п+ 1) Ах час. Толщина слоя Д* вы­бирается произвольно. Уравнение (134) будет давать результа­ты тем точнее, чем меньше выбрана толщина слоя Ах. Вообще достаточно рассматриваемую стенку разделить на 4—5 слоев толщиной Д* м.

Простейшее решение уравнения (146) возможно в том случае, если даны температуры поверхностей стенки. При этом допустимо

Любое изменение температуры поверхности за весь период рас­сматриваемого промежутка времени (п+1) Ат час., что нисколько не затрудняет определения температурного поля. Это является существенным преимуществом данного метода по сравнению с точным аналитическим расчетом. Но, если температуры обеих поверхностей не даны, а известна лишь (любая переменная)

Температура окружающей среды, то температуру поверхности

Находят из приближенного уравнения

«Д**Г +*•&». Дт. Д* ор ' /Но

0 “---------------------------------------------------- с - (148)

VfiAT. O

JnA TtAx

	^пйт, тйх
УпйТ,(т+і)йх
Рис. 12. Распределение темпера­тур в слоях стенки в момент времени лЛт час.
УяАсМх

ИЛИ

= п Дт == Дт, (т + 1) Д X дТ( т д * + дТ§ (/л — 1) Д х * (151)

Подставляя уравнения (149) — (151) в уравнение (145), получим

^(п 4- 1) Дт, т Д х Дх, т Д____ х

Ат

(152)

= а

^п Дт, (т + 1) Д х Дт, т Д х ~Ь Дт, (т — 1) Д х

Дх2

Это уравнение связывает все значения 0(/г + 1)Дт» т. е. температуру, отмеча­емую спустя (л+1)Дт час с температурой ^лдт, которая была раньше в Дх час. Благодаря этому можно определит^ изменения температурного поля во времени. Найденное уравнение существенно упрощается, если считать, что

2а]Дт = (Дх)2,

Как это было сделано в уравнении (147). Тогда уравнение (152) преобразует­ся в искомое уравнение (146).

Как показывает примерный расчет, для определения температур наруж­ных поверхностей стенки д 0,о недостаточно лишь уравнения (146). Их можно определить различными способами по температуре окружающей сре­ды $г и коэффициенту теплоотдачи а. Количество передаваемого тепла по уравнению (2)

(153)

С другой стороны,

(154)

Вычитая одно уравнение из другого, находим искомую температуру поверх пости »

-I

(155)

Для решения этого уравнения необходимо знать температурный перепад на поверхности. В большинстве случаев это невозможно. Чаще бывает известно количество передаваемого тепла. Тогда по уравнению (154) искомая темпе­ратура поверхности

(156)

В большинстве случаев не известны ни ц, . Но всегда из уравнения (146)

А»

Известна расчетная температура §п д х> Д;г зафиксированная в точке, распо­ложенной на расстоянии Ал: м от поверхности. Тогда средний температурный перепад между этой точкой и поверхностью составит

Дт, О Дт, Д. у

Подставляя это выражение в уравнение (155), получим

».4,, о =»г—7 &ПАТ'°д^АТ'А*- °С. (158)

Решая это уравнение относительно д т>0( определяем искомую температуру поверхности

ЯА х & —|— д д „

А ________ Г 1 Л Дт, Д X /1ГЛ

Л Дт, о------------ —----------------- °с. 159)

• Х + а-Д*

Е. Шмидт применяет несколько иной, графический метод определения температуры поверхности, отличающийся от приведенного выше *.

, * (Кроме метода Шмидта, разработаны еще другие методы приближен­ного решения задач теплопроводности. Например, методы, предложенные

A. П. Ваничевым и П. П. Юшковым. Метод А. П. Ваничева разработан при­менительно к трехмерной задаче для тела, физические свойства которого из­меняются с температурой. Метод П. П. Юшкова позволяет получить, реше­ния не только с учетом изменения физических параметров с температурой, но с учетом еще возможного переноса вещества в процессе. Следовательно, оба указанных метода обладают большей общностью, чем метод Шмидта, и дают* кроме того, более точные результаты при меньшей затрате времени на рас­четы.

Представляют значительный интерес решения задач теплопроводности, основанные на методе так называемых аналогий. Здесь используется основ­ное положение о том, что «Единство природы обнаруживается в поразитель­ной аналогичности» дифференциальных уравнений, относящихся к различ­ным областям явлений» (Ленин В. И., Материализм и эмпириокритицизм).

Аналогии процессов нестационарной теплопроводности с электрическими и гидродинамическими явлениями, которые являются более управляемыми, позволили создать счетно-решающие приборы, получившие названия соответ­ственно электроинтегратора Л. И. Гутенмахера и гидроинтегратора

B. С. Лукьянова. Эти приборы дают возможность осуществлять приближен­ное интегрирование не только дифференциальных уравнений теплопроводно­сти, но и других уравнений математической физики, относящихся к различ­ным областям техники, с точностью вполне достаточной для технических4 це­лей.