§ 1. Постановка задач о синхронизации; основные

термины и определения

Попытаемся дать достаточно общую математическую форму­лировку задач о синхронизации, с тем чтобы охватить по возмож­ности большее число встречающихся частных случаев. Попутно разъясним используемые далее термины и приведем основные определения.

Ограничимся прежде всего изучением синхронизации так на­зываемых динамических систем, основное свойство которых за­ключается в том, что их состояние характеризуется некоторым

Рис. 4.

набором параметров (фазовых координат), причем задание зна­чений этих координат в некоторый фиксированный момент вре­мени полностью определяет значения координат в любой момент времени. Более точные формулировки понятия динамической системы можно найти, например, в монографиях [218, 220].

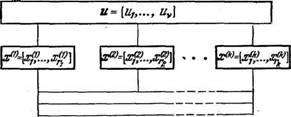
Рассмотрим некоторое число к динамических объектов, свя­занных друг с другом в единую систему (рис. 4). Пусть состоя­ние 5-го объекта определяется г,-мерным вектором... •••, 4f] (s = 1, . . ., к), компоненты которого XjS) являются координатами объекта в фазовом пространстве системы.

Состояние системы в целом определяется как совокупностью векторов так И V-мерным вектором и = [Щ, . . ., Mvl,

характеризующим состояние системы связи между объектами. Таким образом, фазовое пространство всей системы имеет I = Г| +______ + rh + v измерений.

Будем говорить, что система совершает синхронное движе­ние, если ее фазовые координаты изменяются по закону

^•s) = nftot - j - y^s) (mjsW) (/ = 1, .. •, rs; s = 1, ..., k),

(1.1)

Up = npod -}- Vp (nipb>t) (p = 1, ..., v),

^<s) ^

где (о — положительная постоянная, п$ и np — целые числа, rr^p и nip — целые положительные числа, а у^ и v(1 — периоди­ческие функции соответственно с периодами 2п! т{р и 2п/те но <at (т. е. также с общим периодом 2л по cot); числа|n)s)|, и тр можно, не нарушая общности, считать взаимно про­стыми. В случае, если і какое-либо число raj[6] или щ равно ну­лю, соответствующую координату xs) или Up будем условно называть колебательной, а в случае ф0 или щ’Ф10 — вращательной.

Наличие вращательных координат характерно для механиче­ских систем; при этом вращательной координате в реальной си­стеме может отвечать не обязательно вращение тела, а любое равномерное в среднем движение (например, прямолинейное движение с постоянной средней скоростью).

Поскольку согласно (1.1) имеем[7])

<ж'8)> = па)ы, <Мр> = Пр(0, (1.2)

то Ьинхронным движениям системы отвечают колебательные или «равномерные в среднем» движения по каждой из фазовых коор­динат с одинаковыми для всех координат или кратными часто­тами (средними угловыми или линейными скоростями).

Если все числа njs) равны 0, +1 или — 1, а все числа равны 1, то будем говорить о простых, а в противном случае — о кратно-синхронных движениях. Соответственно будем разли­чать задачи о простой и о кратной синхронизации динамических объектов. Величину со > 0 назовем синхронной скоростью (ча-

стотой).

Если система связанных объектов при определенных услови­ях допускает хотя бы одно устойчивое синхронное движение[8]), то будем говорить, что объекты при этих условиях обнаружи­вают тенденцию к синхронизации: если при некоторых условиях движение системы при t-* 00 неограниченно приближается к не­которому синхронному движению, то будем говорить, что объек­ты при указанных условиях синхронизируются.

Во многих случаях поведение динамических объектов и си­стем связи между ними удается адекватно описать посредством дифференциальных уравнений, которые согласно структурной схеме (см. рис. 4) могут быть записаны в следующем характер­ном виде:

где

— соответственно г,- и v-мерные вектор-функции, удовлетворяю­щие весьма общим требованиям, при которых система (1.3) явля­ется динамической, и некоторому специальному требованию, ко­торое будет указано ниже. Вектор-функции F и U, характери­зующие связи между отдельными объектами, назовем функция­ми связей.

Из структурной схемы системы, а также из уравнений (1.3) видно, что каждый из объектов может быть связан со всеми прочими как непосредственно, так и через систему связи, состоя­ние которой как раз и. характеризуется фазовыми координата­ми Up. Вместе с тем из уравнений видно, что координаты определяющие состояние объектов, И координаты Ир системы связи, по существу, входят в уравнения (1.3) вполне «равноправ­но». Характерная для многих задач о синхронизации специфика каждой группы переменных выяснится ниже.

Под. основной задачей теории синхронизации будем понимать установление условий существования и устойчивости решений

уравнений (1.3), имеющих вид (1.1). т. е. решений, отвечающих синхронным движениям.

Конкретизируем теперь вид правых частей уравнений (1.3). Будем предполагать, что функции f)s) и U9 зависят от

своих аргументов таким образом, что носле подстановки вместо. х(р и Щ их выражений согласно формулам (1.1) эти функции становятся периодическими функциями «безразмерного време­ни» т — cat с периодом 2п.

Последнее условие не является обязательным для существо­вания у системы (1.3) синхронных движений, однако оно выпол­няется во всех основных конкретных задачах о синхронизации и существенно упрощает их решение; поэтому далее это условие предполагается справедливым. Заметим, что для его справедли­вости достаточно, .чтобы Ajs) и Up были периодическими функ­циями вращательных координат с периодом 2п, а также, быть

может, функциями разностей /ns) — .?4РУпсТ Uj/rij — Up/zip, r(s) /~fs) /~ Ы fpl

з / п:і —ич по - где ■(■■ , ла. Uj н Up — вращательные координаты.

Переходя в уравнениях (1.3) по формулам (1.1) от перемен­ных х, и и t к переменным у, v и т = юt, получаем систему вида

- Г(в) (if(8), х) + Ф<‘> (yW. ..., у<* г, т) (. = 1, ..., к)%

(1.4)

где, в соответствии с предположениями о характере вектор - функций X(s) и U, функции и V являются периодически­

ми относительно безразмерного времени т с периодом 2я.

Таким образом, основная задача о синхронизации сводится к установлению условий существования и устойчивости периоди­ческих решений системы уравнений (1.4), имеющих период 2я.

Помимо сформулированной выше основной задачи о синхро­низации зачастую представляет также интерес решение следую - тцих задач.

1) Реальное вычисление синхронной скорости (частоты) со, •а также решений (1.2), отвечающих устойчивым синхронным движениям. При этом в ряде случаев можно ограничиться опре­делением средних за период 2я значений функций уи) (т) и V (т), т. е. величин

2Л 2П

“(8> = ШГ1 ^'S) dx' “ = 2ЇГ J v dx’ (1-5)

о о

а также максимальных отклонений | У'Р (т) — cif * 1,пах и |ур(т) —

— арі та* ОТ ЭТИХ СреДНИХ ЗНЭЧеНЯЙ.

2) Выбор системы связи, при котором обеспечиваются суще­ствование и устойчивость синхронного движения (1.1) заданного вида. Эта задача, которую можно назвать задачей синтеза, явля­ется в известной мере обратной по отношению к основной.

В ряде случаев представляет интерес также решение весьма трудной задачи об определении в фазовом пространстве системы таких областей начальных зпачепий ее координат («областей захвата»), для которых с течением времени движение неограни­ченно приближается к определенному синхронному движению.

Естественно, что для возможности использования явлений синхронизации необходимо, чтобы время установления синхрон­ного режима было не слишком велико, а основные характери­стики синхронного движения обладали достаточной «стабильно­стью» по отношению к разного рода погрешностям изготовления системы. Поэтому существенное значение в связи с некоторыми приложениями представляет оценка времени практического уста­новления устойчивого синхронного режима при заданных началь­ных условиях, а также оценка «чувствительности» этих харак­теристик синхронного режима в системе по отношению к изме­нениям параметров объектов и системы связи, а также по отно­шению к постоянно действующим возмущениям.

Один из наиболее важных классов задач о синхронизации образуют задачи о синхронизации автоколебательных объектов, т. е. > объектов (как правило, однотипных), каждый из которых, будучи изолирован от остальных (функции связей F(s) и Ф(<!) соответственно в уравнениях (1.3) и (1.4) отсутствуют), при оп­ределенных условиях может совершать движения типа (1.1), характеризующиеся некоторой частотой (угловой скоростью) со». Величину озs естественно назвать парциальной частотой (скоро­стью) объекта *). Задача о синхронизации при этом заключается в установлении условий, при которых после объединения всех объектов в единую систему последние могут совершать движе­ния того же типа, но с одинаковой частотой (скоростью) со или же с частотами (скоростями) вида п„а.

В зависимости от характера постановки задачи о синхрони­зации автоколебательных объектов или систем, содержащих та­ковые, следует различать задачу о внутренней (взаимной, авто­номной) синхронизации и задачу о внешней (неавтономной) син­хронизации.

В первом, наиболее общем случае, к которому и относилась приведенная выше постановка задачи о синхронизации, все синхронизируемые объекты рассматриваются как равноправные

*) Применительно к определенным типам объектов понятия о парци­альных частотах (скоростях) будут ниже уточнены и конкретизированы (см. § 5 гл. 3, § 1 гл. 5 и § 2 гл. 6).

3 И. И. Блсхман

элементы единой автономной динамической системы; частота синхронного движения о при этом устанавливается в результате взаимодействия всех элементов системы. Правые части уравнений

(1.3) в таком случае не содержат в явной форме время t, а зна­чение синхронной частоты ю заранее неизвестно и подлежит определению в процессе решения задачи.

Во втором случае предполагается, что один из синхронизи­руемых автоколебательных объектов является значительно более мощным по сравнению со всеми остальными, и поэтому его дви­жение считается не зависящим от характера движения прочих элементов системы. Воздействие указанного объекта на осталь­ные элементы системы и, тем самым, частота (или угловая ско­рость) синхронного движения предполагаются наперед заданны­ми и неизменными. Исходная система (1.3) при этом подходе к задаче обращается в неавтономную, и ее порядок понижается.

Частным случаем задачи о внешней синхронизации является задача о захватывании, когда речь идет о синхронизации под действием задаипого внешнего периодического возмущения од-, ного-единственного автоколебательного объекта. Заметим, что в литературе, говоря о синхронизации, часто имеют в виду имен­но захватывание.

Понятие о синхронизации предполагает возможность (и целе­сообразность) выделения в единой системе нескольких объектов, состояние которых характеризуется «собственными» фазовыми координатами. Между тем такое расчленение системы на «объ­екты» и «связи» в принципиальном отношении достаточно услов­но; это вытекает, например, из того обстоятельства, что если не сделано никаких оговорок о характере функций связей F(s) и Ut то все переменные входят в систему уравнений (1.3) вполне равноправно.

Однако при рассмотрении конкретных задач о синхронизации обычно не возникает вопроса о выделении отдельных объектов. Дело здесь не только (и не столько) в том, что эти объекты йредставляют собой обособленные физические или биологические системы (маятники, электрические генераторы, насекомые и т. п.), а в том, что связи между отдельными объектами в практически интересных случаях значительно слабее, чем между отдельными элементами самих объектов (см. § 2).

При наличии сильных связей между объектами их выделение (по крайней мере при математическом решении задачи) часто нецелесообразно, и явление взаимной синхронизации ничем не выделяется из класса автоколебательных явлений.

В технике иногда различают самосинхронизацию и Принуди­тельную синхронизацию. В первом случае имеется в виду, что синхронизация и требуемые соотношения между фазами колеба­ний и вращений осуществляются естественным путем, т. е. под действием уже имеющихся в системе связей. Так, например, син­хронизация генераторов электрических или механических коле­баний (вибровозбудителей) часто происходит за счет свойств самой системы генераторы — нагрузка. Во втором случае для получения эффекта синхронизации или требуемой фазировки требуется введение дополнительных связей.

Заметим, что при рассмотрении ряда конкретных задач вы­ражения (1.1), характеризующие синхронные движения, удобнее записывать в следующей форме:

•*j?) = CTiS) [?iS4SW + v f (m-s)wf)] (7 = 1, ..., rs; s = 1, ..., jfc),

(1.6)

mp - 0fp tepRptof + vp (nipat)] (p = 1, ..., v).

Здесь в отличие от (1.1) целые числа «jS> и пр предполагаются положительными; о — числа, любое из которых может быть равно +1 или — 1; g)s> и др — числа, равные либо 1, либо О <в первом случае, согласно приведенному ранее определению, соответствующая координата является вращательной, а во вто­ром — колебательной). Прочие обозначения в формулах (1.6) имеют тот же смысл, что и в (1.1).

В небесной механике наряду с термином «синхронизация» часто используют термины «резонанс» или «соизмеримость сред­них движений». При этом под таковыми понимают наличие меж­ду средними угловыми скоростями вращательных движений объектов о, линейных однородных соотношений

^2,РЮ2 + • - • + — О (4 п

(р = 1, д^к* — 1)

С целочисленными коэффициентами rijp, причем число таких со­отношений (предполагаемых линейно независимыми) не превы­шает к* — 1, где к* — число рассматриваемых вращательных движений.

Нетрудно убедиться в том, что определение синхронных дви­жений в виде (1.1) охватывает определение, основанное на «ре­зонансных соотношениях» (1.7). Действительно, если справедли­вы равенства (1.1), то согласно (1.2) (Oj —h}<o, где щ — целые числа, и поэтому между величинами o)j существует не более к* — 1 независимых равенств типа (1.7). С другой стороны, как легко убедиться, соотношения типа (1.7) всегда можно удовлет­ворить выражениями типа щ = и3-(о, причем при так называе­мом «полном резонансе», когда д = к*~ 1, это можно сделать единственным (с точностью до несущественного множителя) 3*

образом [9]). а при «неполном резонансе» (q < к* — 1) — бесчис­ленным числом способов. Так, известное соотношение (см,, на­пример, [100])

«і — Зсо2 + 2м3 = 0 между «средними движениями» (средними угловыми скорости-

е О О О

ми) спутников Юпитера Ио, Европа и Гаиимед (мь со2 и и3 соответственно) в принципе могло бы осуществляться при ©і = ©2 = «з = со, при й] = — и, 0)2 = о), со2 = 2оэ, при 0)х = 4со,

° о

щ = 2(0, 0)3 = о) и т. д.

Итак, с формальной точки зрения, между случаями соизмери­мости частот (кратной синхронизацией) и наличия резонансных соотношений (1.7) нет принципиальной разницы. Следует, одна­ко, иметь в виду, что обычно наибольший прикладной интерес представляют случаи, когда целые числа |njS) |, |rp|, п mv, а также числа niv сравнительно невелики: большим значе­ниям указанных величин обычно отвечают малые области суще­ствования и устойчивости, а также малые области притяжения соответствующих режимов (см. § 3 Введения). При учете этого обстоятельства различение кратной синхронизации и синхрони­зации в смысле наличия резонансных соотношений может иметь смысл. Например, случай сої = ЮОсо, 0)2 = 102о), а>з = О) есте­ственно рассматривать как синхронизацию при наличии резо-

о о о

нансного соотношения 0)2 — 0)i = 2со3.

В радиофизике иногда говорят о синхронизации на комбина­ционных частотах,. имея в виду установление целочисленных со­отношений (соизмеримости) не между самими частотами а между их линейными комбинациями с целочисленными коэф­фициентами, например, между разностями — и j.

Для некоторых приложений может оказаться целесообразным расширить приведенное выше понятие синхронизации, распро­странив его на объекты более общей природы и охватив более общие типы движений. Так, например, можно ограничиться тре-

бованием, чтобы вид (1.1) или (1.6) имели лишь выражения по крайней мере для одной из координат объектов Можно

предполагать также, что функции уj-s) и ve являются почти пе­риодическими. Наконец, можно исходить из значительно более общего определения синхронизации, понимая под таковой ра­венство некоторых функционалов от координат объектов, напри­мер, совпадение моментов времени, когда: эти координаты обра­щаются в нуль, достигают экстремальных значений и т. п. Кац правило, достаточно ограничиться изложенным выше менее об­щим толкованием синхронизации, когда за указанные функцио­налы принимаются частоты (или средние скорости изменения координат объектов).

Заметим, что приведенное вътше и используемое всюду далее определение синхронизации, которое с /самого начала предпола­гает выделений в системе однотипных объектов, можно условно назвать физико-техническим. Имеются более абстрактные Опре­деления, ле предполагающие такого выделения объектов (см., например, [109]); подобные определения можно назвать матема­тическими.

Укажем также, что для ряда приложений представляет инте­рес задача о синхронизации в системах с распределенными пара­метрами. В этом случае в числе уравнений типа (1.3) содержатся уравнения в частных производных.