В механике твердого тела такие явления, как пластич­ность и ползучесть, а также относительно большие перемеще­ния, приводят к нелинейным задачам, в которых параметры ис­ходных уравнений и краевые условия зависят от искомых функ­ций, поэтому их решение в отличие от решения линейных задач (нацример, линейных задач теории упругости), в общем случае не представим в виде суммы частных решений. Именно поэтому нелинейные задачи решают численно, а не аналитическими мето­

дами.

Физическая нелинейность, т. е. нелинейность связи между напряжениями и деформациями в уравнении (7.31), содержится в условиях текучести и ползучести. Действительно, матрица [D] в этом уравнении зависит от достижения уровня напряжений и деформаций, как видно из функциональной схемы

№[И(ч>МШМФ)]=Мад)1 - (7.35)

Искомым решением нелинейной задачи является решение со­ответствующей линейной задачи при таком подборе параметра ijj (который на текущем этапе нагружения является только функци­ей координат х, у, г,), чтобы удовлетворялось соотношение (7.31). При решении целесообразно использовать метод итера­ций (метод последовательных приближений)

где (п'іДл-Л - номера итераций. Здесь мы пришли к извест­ному методу переменной жесткостиі так как при итерациях под­бираем матрицу р>(^)] • 3 принципе можно было подбирать и

[е0} в уравнении (7.31).

Итерационный процесс (7.36) нашел применение в следую­щей форме:

X) при упругом нагружении или разгрузке, когда

*гпЧ,< МЛ.

fи=Р f *' °+ (Ьр)[^+Ф(бГ ‘ т) ді] ; (7.37а)

2) если пластические деформации не изменяются и не про-

f VS - я t

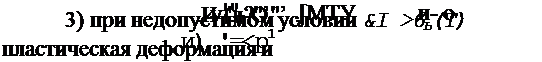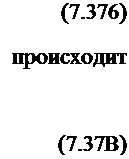исходит разгрузка, т. е. если 0І ' - б5(ту, то

итерационный процесс заканчивается, когда

Здесь - параметры итерационно!^ процесса, опреде­ляющие скорость его сходимости и точность получаемых резуль­татов, CUpil, CUK. il, ff«M, Под б.,(Т) в данном случае

следует понимать некоторый относительно узкий диапазон зна­чений предела текучести (65-Лб5 , 6^+), где.

Подробнее итерационгый процесс будет изложен для случая одно­мерного напряженного состояния (§ 7.3).

Рассмотрим теперь методы реализации геометрической не­линейности.

Ранее предполагалось, что перемещения и деформации свар­ной конструкции малы. Практически это означает, что форма

конструкции в процессе нагружения не изменяется. Однако на практике такие допущения не всегда оправданы. Например, большие угловые деформации при стыковой односторонней сварке могут существенно изменить форму поперечного сечения, в ре­зультате чего может измениться прогиб соединения и, сле-^ довательно, распределение продольных напряжений бх (см. рис. б.б). При несквоэном проплавлении поперечные деформации удлинения ty на стадии охлаждения в зоне непровара (в зоне концентрации деформаций) могут достигать десятков процентов, что также существенно изменит форму этой зоны. Учет измене­ния геометрии тела в процессе деформирования, т. е. учет гео - нетрической нелинейности, приводит к нелинейной задаче, гео­метрическая нелинейность часто может сочетаться с физической. 5 принципе это не приводит к дополнительным существенным трудностям.

Геометрическая нелинейность может быть реализована с помощью следующего итерационного процесса. В качестве на­чальной геометрии тела принимается форма соединения на пре­дыдущем этапе, решается нелинейная задача термопластичности на текущем этапе нагружения, затем форма тела корректируется и процесс - повторяется до тех пор, пока геометрия тела не пе­рестанет изменяться. При этом за геометрию тела следует при­нимать некоторую ее форму в промежутке t-ftt, t (в середине этапа или, что удобнее, в конце его). Поскольку для свароч­ных задач характерна слабая геометрическая нелинейность (ма­лое изменение геометрии на этапе нагружения), то один из удобных приемов ее реализации заключается в том, что итера­ции по геометрии тела и по функции СОСТОЯНИЯ f происходят одновременно.

При относительно малых приращениях деформации на каждом этапе нагружения можно принимать, что форма тела на текущем этапе не изменяется и определяется конечным состоянием на предыдущем этапе.

Таким образом, на каждом шаге прослеживания за историей нагружения и каждой итерации по функции состояния if и гео­метрии тела возникает линейная задача, которая соответствует задаче теории упругости, если под [D] , [йе.} и {є0} в урав­нении (7.31) условно понимать соответственно матрицу упруго­сти [D] , деформации [Ц и температурные деформации 1ет} в

уравнении (?.33). Решение полученной линеаризованной задачи для случая одномерного напряженного состояния не представ­ляет труда, оно будет рассмотрено в § 7.3. О методе решения двумерной линеаризованной задачи будет сказано в подпара­графе 7.4.4.