Теория кодирования — раздел теории информации, изучающей способы отож­дествления сообщений с отображающими их сигналами. Кодирование применяют при передаче, хранении и преобразова­нии информации. Для кодирования сооб­щений используют набор символов. Мно­жество символов называют алфавитом кода: {Ai, аг, . . ., ат}.

Количество символов в алфавите обозначают буквой m и называют осно­ванием кода. Десятичная система счис­ления является кодом с основанием ш— 10 (т. е. количество значащих цифр равно десяти). При этом значащие циф­ры (их форма, вид) составляют алфавит: 0, 1, 2, 3, .. ., 9. С помощью алфавита (значащих цифр) в системе счисления можно выразить (закодировать) любую числовую величину.

Код Морзе имеет основание т = 2; следо­вательно, его алфавит состоит из двух симво­лов — точки и тире {. —}. Выражение звуков языка тоже осуществляется определенным кодом. Так, для русского языка основание кода т — 33, а алфавит состоит из букв а, б, в, г, . . ., я.

Любую упорядоченную выборку сим­волов из алфавита называют кодовым. словом или кодовой комбинацией: В = = {а,-1, а, 2, . . ., Ain).

Количество (число) символов в кодо­вой комбинации обозначают буквой п и называют длиной кодовой комбинации.

Кодом называют любое упорядочен­ное множество кодовых комбинаций: {Bl, Й2, • • ., вД,}.

Количество (число) кодовых комби­наций в коде называют мощностью или 14 Объемом кода. Максимальная мощность кода N = Mn.

Представление информации кодом.

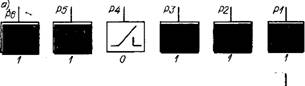
Элементы, положения, события и т. д., для которых характерны два устойчивых и противоположных состояния, удобно описывать кодом с основанием пг = 2. Например, контакты реле могут быть замкнуты или разомкнуты, триод открыт или закрыт, деталь на станке установ­лена или снята, привод включен или вы­ключен, самолет обнаружен или не обна­ружен и т. п. Если одному состоянию элемента (положения, события) припи­сать значение 1 (единица), а другому 0 (нуль), то алфавит кода будет содержать всего два символа (знака) — 0 и 1, а ко­довая комбинация — набор символов из этого алфавита. Например, режим вклю­чения шести реле (Pi), определенный кодовой комбинацией 110111 (рис. 1.2, а), будет означать, что в заданный момент времени лишь контакты реле Р4 не будут замкнуты. Комбинации 110000, 010001 и 111111 означают, что сработали соот­ветственно шестое и пятое, первое и пя­тое, все реле и т. д.

Рассмотренную информацию можно записать на бумаге символами 1, 0 (рис. 1.2,6) или представить на бумаж­ной ленте комбинацией отверстий (рис. 1.2, в), считая пробитое на ленте отверстие за 1, а отсутствие за 0. Распо­ложение отверстий в строке на соответ­ствующих дорожках определит состоя­ние рассматриваемых элементов. При этом полагают, что первая дорожка (счет справа налево) определяет состоя­ние первого реле, вторая — второго, третья — третьего и т. д.

В данном случае длина всех рас­смотренных комбинаций (110111, 110000 и т. д.) равна шести (п — 6).

Дорожки 1-6

Р1

Ш

1

Л= ли

■ ■■■■■

111111

Я в) © © © © © &

0000 О О О С Р5 Р4 Р3 Р2 Р1

110111

1 О

110000

010001

О О

111111

1 о

Р6 Р5 Р41 АЛ Р2 Р1

101101

■ ■ ■

1 о

Рис. 1.2. Представление информации кодом с основанием т = 2; (рб

А — состояния элемента реле; б — запись символами; в — пред - V______________ Jt

'<йр<й)©<5)

Ставление на перфоленте отверстиями

Количество единичных символов в комбинации называют ее весом и обозна­чают /. Комбинация 11001 имеет вес 1 = 3, комбинация 11111 — вес 1 = 5, ком­бинация 00010 — вес / = 1.

Кодовым расстоянием D между двумя комбинациями называют количество не­совпадений их разрядов. Например, ко­довое расстояние между комбинациями 10000 и 11000 будет D = 1, между комби­нациями 11100 и 00011 — D — 5. В первом случае все разряды одинаковы, кроме одного, во втором случае различны все пять разрядов.

Классификация кодов. Имеется боль­шое число признаков классификации ко­дов. Назовем основные из них.

1. По основанию: коды с основанием т = 2 называют двухпозиционными, с основанием ш> 2 — многопозиционны­ми.

2. По длине кодовых комбинаций: коды равномерные, если п = const, и не­равномерные, если п Ф const.

3. По весу комбинаций: коды равно­весные (или коды на одно сочетание), Если / = Const, и неравновесные (или коды на сумму сочетаний), если 1ф Const.

Символом

Равновесный код называют также ко­дом I из п. Число комбинаций кода равно числу сочетаний из п по I и обозначается /п

Из комбинаторики из-

Вестно, что

П_—1) (л —2) ... (n — l+ 1)

I

U

В технике широкое применение имеет код 2 из 5, число комбинаций этого кода

5-4 2 ~

Все комбинации кода имеют одинако­вый вес 1 = 2.

Код на сумму сочетаний содержит комбинации различного веса. В общем случае вес п членной комбинации изме­няется от 0 до п, сумма комбинаций равновесных кодов (формула бинома

Ньютона)

Для п = 5 общее число комбинаций

+ (б) = 1+5+10+ 10 + 5+1 =32.

4. По способу упорядочения комбина­ций. Число вариантов упорядочения рав­но числу переставок из N, равному N1. Таким образом, имеется 10! кодов 2 из 5.

Пример одного из вариантов комбинаций:

0) 11000; 1) 10100; 2) 01100;

3) 01010; 4) 00110; 5) 00101; 6) 00011; К С[2]' 7) 10010; 8) 10001; 9) 01001. J

5. По четности или нечетности веса комбинаций. Если все комбинации кода имеют четный вес, то код называют четным, если нечетный вес — нечетным.

Пример четного кода:

0) 0000; 1) ООП; 2) 0101; 3) ОНО; 1 м

4) 1001; 5) 1010; 6) 1100; 7) 1111. J к '

6. По числу комбинаций заданной длины. Если код содержит все возмож­ные комбинации заданной длины (N= = 2"), то его называют полным или кодом Безызбыточности. Если код содержит только часть этих комбинаций, то его на­зывают неполным или кодом с избыточ­ностью. Избыточность необходима для придания коду каких-либо особых свойств, в частности помехозащищенности.

Код (1.2) будет неполным, поскольку при его формировании использовали только восемь комбинаций (четного веса) из возможных 16. Из оставшихся восьми нечетных комбинаций можно, в свою очередь, образовать также неполный нечетный код.

7. По кодовому расстоянию. Код с постоянным кодовым расстоянием (d = = const) между смежными комбинация­ми называют переменным.

Код 2 из 5 [см. (1.1)] является двух - переменным. Кодовое расстояние между смеж­ными комбинациями этого кода всюду равно двум. Те же десять комбинаций можно рас­положить по-другому и получить четырехпере - менный код:

0) 00011; 1) 11000; 2) 00110; 3) 10001; 4) 01100; 5) 10010; 6) 01001; f (1.3) 7) 10100; 8) 01010; 9) 00101. )

8. По арифметическим свойствам ко­да. С помощью различных кодов записы­вают числа. Код, обладающий арифмети­ческими свойствами, называют арифме­тическим. Комбинации такого кода мож­но рассматривать как числа и произво­дить с ними различные арифметические операции.

Если код не обладает арифметиче­скими свойствами, его называют комби­наторным. Комбинаторные коды форми­руют по законам теории соединений (со­четаний, размещений, перестановок), изучаемой в разделе математики, назы­ваемом комбинаторикой. Из рассмотрен­ных кодов к комбинаторным относят рав­новесные, четные, нечетные.