Определим напряжения, исходя из допущений, что: 1) горизонтальные составляющие радиальных сжимающих напряжений от реактивных сил на контактных поверхностях матрицы и пуансона одинаковы по величине; 2) напряжения – продольные – равномерно распределены по сечению заготовки, 3) материал не упрочняющийся, 4) конусность пуансона не принимается во внимание.

Процесс рассматривает как плоскую схему деформированного состояния (рис.18.4).

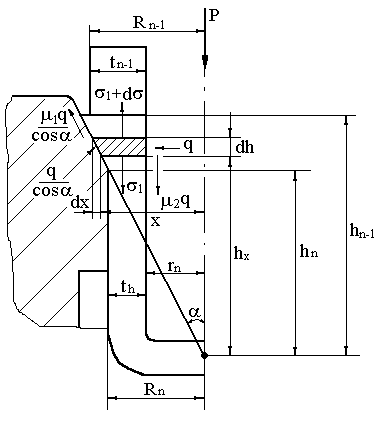
Рис. 18.4 Схема к определению напряжений при вытяжке с утонением.

Уравнение равновесия выделенного элемента в очаге деформации с внешним диаметром , высотой 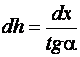и площадью поперечного сечения будет:

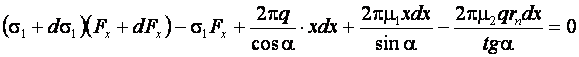(18.1)

После преобразований:

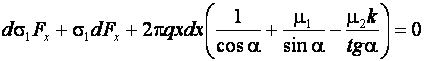(18.2)

Где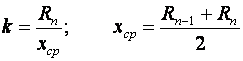

Обозначая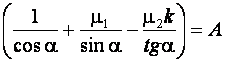

И принимая во внимание, что

Получим:

(18.3)

Условие пластичности для данного случая:

или (18.4)

Решая совместно уравнение равновесия и пластичности, после интегрирования имеем:

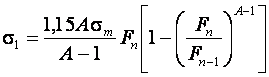(18.5)

Где - среднее сопротивление деформированию.

Усилие вытяжки будет:

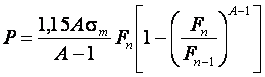(18.6)

Напряжения и усилия могут быть определены с помощью формул, предложенных Е. А. Поповым:

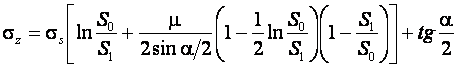(18.7)

И

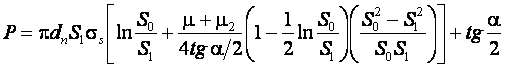(18.8)

Где и - исходная и конечная толщина стенок; и - коэффициенты трения, соответственно, на матрице и пуансоне, - угол конусности матрицы, - диаметр пуансона.