Молекулярная структура и теплоемкость углеродистых кристаллических веществ
 17 апреля, 2013
17 апреля, 2013  admin
admin Для облегчения приведенного в последующих разделах анализа связи между теплоемкостью и структурой твердых горючих ископаемых целесообразно кратко остановиться на применении изложенной выше теории теплоемкости к простым высокоуглеродистым полимерам — графиту и карбину, так как они представляют основные устойчивые формы структурной организации углерода, элементы которых могут присутствовать в более сложных структурах.
Графит. Кристаллическая решетка природного графита составлена из параллельных слоев, образованных сетками правильных шестиугольников, в узлах которых локализованы углеродные атомы. Расстояние между ближайшими соседями в слое составляет 1,415-ІО-10 м, расстояние между слоями — (3,354—3,357) 10-10 м.
Известны две модификации природного графита — гексагональная и ромбоэдрическая, различающиеся последовательностью чередования слоев. Физические свойства обеих модификаций весьма близки.
Жесткие межатомные связи внутри слоя, образованные при помощи 5/72-гибридизации валентных электронов, превращают ■его в отдельную макромолекулу, которая удерживается в равновесии со своими соседями сравнительно слабыми силами Ван-дер-Ваальса. Этим обусловлена сильная анизотропия мо - локристаллического графита, проявляющаяся в его механических, теплофизических и других свойствах.
Как отмечалось выше, для оценки структурной прочности кристаллов можно применить параметр 0о (характеристическая температура). При этом большим значениям 0о отвечает "большая жесткость взаимодействия между элементами структуры, а значит, и большая структурная прочность. Так, структура алмаза характеризуется весьма высокой дебаевской температурой (1910 К)-
Имеющиеся в литературе данные о скорости распространения упругих волн в плоскости графитового монослоя и в перпендикулярном к нему направлении [10] позволяют оценить характеристические температуры межатомного (в слоях) и меж - слоевого взаимодействий. При этом постоянная решетки в первом случае 5о—2,46-10~10 м, а во втором она равна удвоенному межслоевому расстоянию, т. е. 6,70-10-10 м. Расчет по формуле (1.54) дает для планарных колебаний (со смещением в плоскости слоя)
1,39-10*
= 2720 К.
2,46-10*10
Для межслоевого взаимодействия
|
91 К. |
![]() 6,62-10-34 1,27-103
6,62-10-34 1,27-103
|
6,7-10-ю |
![]() 1,38-10-2
1,38-10-2
Полученные величины показывают, что прочность отдельного графитового монослоя исключительно велнка — она того же порядка, что и прочность алмазной структуры. В то же время весьма слабая связь между слоями обусловливает низкое сопротивление графита истиранию и низкую теплопроводность в направлении, перпендикулярном к плоскости слоев (см. ниже).
Поскольку графит является носителем типично «гетероди - намической» структуры, постольку, естественно, он стал одним из первых объектов приложения теории В. В. Тарасова [6]. Имея в своем распоряжении весьма неполные данные о низкотемпературной теплоемкости графита, В. В. Тарасов показал, что они хорошо отвечают квадратичному закону.
Дж. Крамхансл и X. Брукс [11], исследовавшие динамику колебаний решетки графита с несколько иных позиций, пришли к аналогичным результатам, а именно: подтвердили Г3 — закон для предельно низких температур и Т2 — закон изменения теплоемкости при более высоких температурах. Предложенное ими интерполяционное уравнение включает две характеристические 20
Температуры, одна из которых соответствует планарным колебаниям (0п), а другая (0Х)—колебаниям со смещением, перпендикулярным к слою:
Где А (“Т”) ~ двумерная функция Дебая (1.39); значения 0п =
= 2500 К (близкое к вычисленному выше) и 0^=950 К подобраны авторами [11] таким образом, чтобы обеспечить наилучшее совпадение с1 экспериментом.
Воспользовавшись этими значениями и данными об упругих свойствах графита [12], оценим температурные интервалы, в которых, согласно теориям В. В. Тарасова н И. М. Лифшица, должны выполняться зависимости (1-41) — (1.43) и (1.45) — (1.47). Результаты расчетов сведены в табл. 1. 2 и сопоставлены с экспериментальными данными.
|
Таблица 1.2 Характерные температурные интервалы зависимости Су (Т) графита
|
Из табл. I. 2 видно, что теория И. М. Лифшица дает более строгие пределы для той или иной зависимости, которые более приближаются к экспериментальным.
Согласно обеим теориям, при очень низких температурах (ниже 2—4 К) теплоемкость графита изменяется пропорционально кубу температуры. Известно, однако, что при этих температурах ощутимыми становятся вклад электронной составляющей теплоемкости, которая растет пропорционально температуре, и влияние дефектов структуры, искажающих температурную зависимость теплоемкости. Более подробно этот вопрос' рассмотрен в монографии С. В. Шулепова [10].
При умеренно низких температурах в полном согласии с теорией теплоемкости графита возрастает пропорционально Т2. По данным В. Де Сорбо и В. Тилера [13], этот закон без заметных отклонений выполняется в интервале температур 13—54 К. При дальнейшем повышении температуры зависимость СУ(Т) постепенно приближается к линейной.
Значения атомной и удельной теплоемкости графита в интервале 13—300 К приведены в табл. 1.3.
Таблица 1.3
|
Теплоемкость природного графита в интервале 13—300 К [13]
|
При высоких температурах (начиная от комнатных) теплоемкость графита можно рассчитать по эмпирической формуле
Ср=а+ЬТ-ёТ~2, (1.57)
Где а, Ь и g — эмпирические коэффициенты, значения которых по данным некоторых авторов сведены в табл. 1.4.
Таблица 1.4
|
Значения эмпирических коэффициентов в уравнении (1.57)
|
Карбин
Сравнительно недавно синтезированный цепной полимер углерода — карбин — изучен менее подробно. С помощью рентгеноструктурного анализа и ИК-спектроскопии установлено, что он образован из атомов углерода, соединенных в цепи тройными связями ^-гибридизация валентных электронов). Межатомные расстояния вдоль цепи составляют, по-видимому, 2 62-10-10 м, расстояния между цепями — 3,91 -10“10 м [16] и
З,95-10-10 м [17].
И. Б. Рабинович, Б. В. Лебедев [16] и другие исследователи измерили в интервале 80—300 К теплоемкость семи образцов карбина. Во всех случаях теплоемкость его оказалась более высокой, чем графита, хотя теплоемкости отдельных образцов карбина различаются между собой. Для одного из образцов, имеющего наибольшую теплоемкость, в интервале 80— 300 К выполняется линейный закон изменения теплоемкости с ростом температуры:
Ср=0,867• 10-2Г, кал/(г-атом •“ С) =
3, 63-10-27 Дж/(моль-К). (1.58)
В других случаях показатель степени при температуре в разных интервалах изменялся от 1,5 до 1,2. Авторы названной работы склонны объяснять это тем, что часть цепей может оказаться сшитой. Это, естественно, приводит при низких температурах к уменьшению числа колебательных степеней свободы
И, как следствие, к уменьшению теплоемкости и изменению характера зависимости СР(Т).
В связи с этим интересно отметить, что зависимость типа (I. 58) обнаружена у большого числа других линейных полимеров [18], что совпадает с выводами теории В. В. Тарасова. Однако некоторые исследователи отмечают, что вычисленная по уравнению (1.36) теплоемкость в ряде случаев оказывается по абсолютному значению ниже экспериментальной. Возможное объяснение состоит в том, что дополнительный вклад в теплоемкость этих полимеров дают боковые группы. Этот вклад тем больше, чем массивнее боковые группы; он нелинейно изменяется с температурой, и с учетом этого температурная зависимость теплоемкости самого скелета макромолекулы также должна быть нелинейной.
Так как карбин лишен боковых групп, низкотемпературная теплоемкость его должна определяться поперечными колебаниями цепей, преимущественно возбуждающимися при низких температурах. По этой причине точное определение характера зависимости СУ(Т) для карбина представляет большой теоретический интерес. Имеющиеся в настоящее время данные, к сожалению, не дают такой возможности вследствие малой изученности структуры карбина и ограниченного объема экспериментальных данных о его теплоемкости.
Что касается зависимости (I. 58), то пока нет достаточных оснований считать, что она является следствием именно цепного строения карбина, а не обусловлена влиянием каких-либо
неучтенных факторов (например, частичным соединением цепей или участием элементов слоистого строения). Надлежащий учет этих факторов или полное их. исключение могут привести к другой зависимости Су(Т).
|
Ср, кал/(моль- К) |
![]()
|
Ср, Дж/{нш - К) |
![]()
|
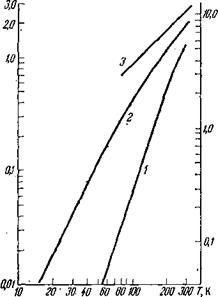
Рнс. 1. Зависимость теплоемкости алмаза (/), графита (2) и карбина (3) от температуры |
![]() На рис. 1 изображена зависимость теплоемкости алмаза, графита и карбина, имеющих одинаковый химический состав, но различное строение, от температуры. Она обусловлена исключительно структурными особенностями веществ.
На рис. 1 изображена зависимость теплоемкости алмаза, графита и карбина, имеющих одинаковый химический состав, но различное строение, от температуры. Она обусловлена исключительно структурными особенностями веществ.

 Опубликовано в
Опубликовано в