Modeling Thermal Stresses and Distortions in Welds
 19 марта, 2014
19 марта, 2014  admin
admin The thermal stress analysis of welds is more complex than the heat flow analysis because of the geometry changes and because of the complex stress-strain relationship. In designing a welding procedure, the critical issues are defects, mechanical properties, distortion and residual stress. Modeling stresses in welds includes all distortions that can be predicted by thermal stress analysis. Models of the mechanical properties of base metal, HAZ and weld metal, are needed as input data for thermal analysis. To evaluate the significance of a given defect, stress analysis is required.
Most thermal stress analyses have used thermo-elasto-plastic constitutive models with rate independent plasticity. Rate independent plasticity implies the viscosity is zero and therefore the relaxation time is zero. This means the stress relaxes instantly to the yield stress. The higher the temperature and the longer the time, the more important viscous deformation becomes. A rate independent model is certainly not valid in the liquid region and is suspect near the melting point where viscous effects are expected to be important; most analyses assume a cutoff temperature. They assume that the thermal strain, Young’s modulus and yield strength do not change above a cutoff temperature. Temperatures above this cutoff temperature are set to the cutoff temperature for the thermal stress analysis. For steels the cutoff temperatures which have been used range from 600-800 °С to 1100-1200 °С.
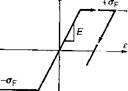
The analysis of stress and distortion in welds involves both rate dependent plasticity and rate independent plasticity. Plastic deformation below half the melting point temperature (measured in degree Kelvin) is usually rate independent plasticity. Stress relaxation by creep or by visco-plasticity is rate dependent plasticity and it should be considered for deformation above half the melting point, in multi-pass welds and in stress-relief of welds. Rate independent plasticity is independent of the deformation rate and therefore of time (in limited deformation rates or the ratio of deformation time to the active plastic deformation). The related characteristic behaviour in a simple one dimensional model is shown in Figure 2-26a.
a
|
a
|
|
Figure2-26a, b: One dimensional model of rate independent elasto-plastic a) and ideal plastic b) of material behaviour; Young’s Modulus E, with yield strength aF; with stress a and strain є, [3]. |
|
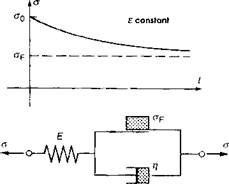
Figure 2-26c: One dimensional model of rate-dependent elasto-visco-plastic material behaviour; relaxation of beginning stress o0 by constant strain є as a function of time t; Young’s Modulus E, with yield strength oF, dynamic viscosity Л. [3]. |
To complete this, Figure 2-26b shows an ideal plastic model which is unsuitable for the evaluation of welding stress. In contrast to this, the elasto-visco-plastic continuum defines a plastic behaviour dependent on the deformation rate and therefore on time. The related characteristic behaviour in a simple one dimensional model and the relaxation behaviour are illustrated in Figure 2-27.
|
STRESS, pSi
|
|
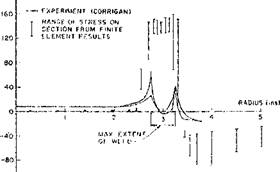
Figure 2-27: Residual longitudinal stress on the top surface vs. transverse distance from the weld centerline in HY-130 weld measured by Corrigan and computed by Hibbitt & Marcal [29] are shown in a). Note the lack of agreement between computed and measured stresses. The longitudinal stress shown in b) was computed by Oddy et al. [60] for HY-80 for three cases. The top curve ignores the phase transformation. The bottom curve includes the volume change due to the transformation. The middle curve includes the effect of transformation plasticity (In steel welds during the austenite-ferrite phase transformation the variations of stress and strain on the length scale of microstructure produce an important contribution to the plastic strain called transformation plasticity). Note the good agreement between experiment and the computed results for the middle curve. |
Although the accuracy is limited by computational costs to rather coarse meshes, Figure 2-13, the residual stresses have usually agreed well with experimental results. An important exception has been the predicted residual stress in high strength steels. Hibbitt and Marcal
[29] attempted to predict the residual stress in welding HY-130 steel. Their results were so different from experiment that they concluded that an important physical phenomenon had been missed, Figure 227.
In 1988, Oddy A. et al. [60] repeated the analysis but included the effect of the austenite to martensite transformation. They obtained the correct residual stress and showed that the critical phenomenon missed by Hibbitt and Marcal was transformation plasticity. This is the plastic strain that occurs during a phase change in the presence of a deviatoric stress.
Transient 3D thermal stress analyses of welds have been described in detail in several papers [53, 56 and 65]. The thermal strain rate due to the transient temperature field induces an elastic, plastic and transformation plasticity strain rate. An exact solution to a stress analysis problem satisfies three basic laws; the conservation of linear momentum or the equilibrium equation, the constitutive relation between stress and strain and the compatibility relations between strain and displacements which is the conservation of mass. In addition it satisfies two types of boundary conditions; the prescribed displacements or essential boundary conditions and the prescribed tractions or natural boundary conditions. A displacement FEM formulation is used to solve the constitutive, compatibility and equilibrium equations. The displacements, rotations and strains are large, transient and 3D. The thermal strain must be modeled with care (Oddy et al [65]) to avoid an incompatibility between thermal strain and strain from the displacement field.
Residual stress and distortion of welds are strong functions of plasticity. We are more concerned with the neighborhood of arc welds that have a small pool of liquid metal as distinct from the structure being welded.
Near the weld pool the kinematics is definitely 3D. Farther from the weld pool, the kinematics in appropriate structures sometimes can be modeled with plane or shell models. The plane strain model was often used in the past, because it is computationally cheap.
During a phase transformation, the volume change induces a local variation in the stress field. For example, during the austenite to martensite transformation, the volume change could place a martensite grain in compression and some of the surrounding austenite in tension just at its yield stress. If an average tensile stress is superimposed upon this microscopic stress field, the austenite could now yield in tension with an infinitesimal applied tensile stress. Now reverse the order. Apply an infinitely small macroscopic tensile stress first. Then transform some austenite to martensite to reach the yield stress of austenite locally. An additional transformation will cause plastic strain. This additional plastic strain is defined to be transformation plastic strain. It will stop when the transformation stops. It arises from the interaction between the microscopic and macroscopic stress fields. This two-scale or multiscale is a bit similar to turbulence models in fluid flow that also use an average or macroscopic velocity and velocity fluctuation. If the macroscopic stress field is not modeled (i. e., the microscopic stress field is modeled directly), then classical plastic strain describes the deformation, and transformation plasticity does not occur. While the classical plastic strain rate is proportional to the deviatoric stress rate, the transformation plasticity strain rate is proportional to the product of the deviatoric stress times the transformation rate of the phase change. It is not creep because it is not proportional to time. Leblond’s exposition of this theory is beautiful [57].
The high temperature range (Г > 0.5Tm ) is usually considered to
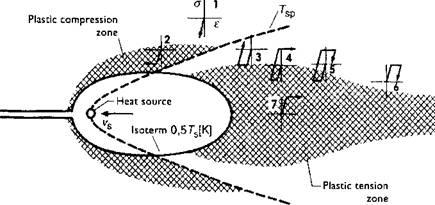
be of minor importance in generating residual stress due to the low value of yield stress. However it is important in hot cracking that is caused by the high temperature strain close to the molten temperature. The geometric changes at high temperatures are inherited by regions that cool from high temperatures. These geometric changes can be very important. The thermo-mechanics of causing the residual stress by welding is shown schematically in Figure 2-28. In this figure the scheme of plastic zone distribution for a case of quasi-stationary temperature field caused by a moving line heat source is presented. The parabola-like curve drawn as a broken line separates the region being heated in front of the curve and the region being cooled behind the curve. The region being heated tends to be in compression and the region being cooled tends to be in tension. The elastic unloading zone shown as a strip separates the compressed and tensioned areas. For different points in the area the schematics highlight the strain-stress cycle related to the local load cycle, without considering temperature dependency.
As an example, adopted from Pilipenko [18], the point 6 in Figure 2-28 may be suggested. At first sight the schematic stress - strain cycle in point 6 should have looked like point 5. But the difference is that material in point 6, after reaching some elastic and plastic compression, was ‘annealed’ inside of the material softening isotherm. Points 1, 2 and 3 represent the evolution of stress developed at a point lying at some distance from the weld centreline. First the material is being exposed to elastic compression (point 1), and then, reaching the yield limit, the material undergoes plastic deformation (point 2), followed by elastic unloading (point 3). Point 7 has a peculiar position. It lies on the weld centreline and the material in this point has been subjected only to elastic and then plastic tensioning.
|
Figure 2-28: Plastic compression and tension zones; local stress-strain cycles in quasi-stationary temperature field of the moving heat source, from Radaj [3]. |
The temperature of the metal in welds varies from the boiling temperature to room temperature. The domain includes the liquid weld pool and the far field of solid near room temperature. The liquid is well described as a Newtonian fluid characterized by a temperature dependent viscosity. The temperature of the solid can be considered to be a linear viscous material characterized by a viscosity due to the diffusion of dislocations. From temperatures aboveTVP ~ 0.5or0.8Tm, the solid can be considered to be viscoplastic and characterized by an elasticity tensor, viscosity and deformation resistance. Below Typ, the solid can be considered to be a rate independent plastic material characterized by an elasticity tensor, yield strength and isotropic hardening modulus. Thus the constitutive equation of a material point must be able to change type with space and time during the welding process. The constitutive model is assigned to be rate independent if the temperature is less than TyP, rate dependent if the temperature is in a range 0.5-0.8 Tm and linear viscous if the temperature is greater than 0.8Tm, where Tm is a melting point or solidus temperature in degrees of Kelvin.
The constitutive model type changes as a function of temperature in space and time.
The practical application of a weld simulation with different constitutive equations within the above mentioned temperature areas will be discussed in detail in chapter V.
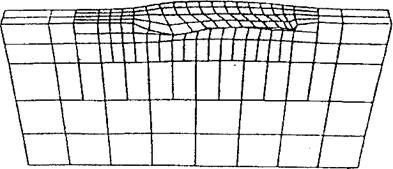
An example of computed displacements in a weld is shown in Figure 2-29.
|
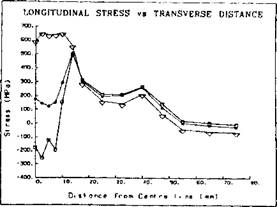
Figure 2-29: Displacements computed by a thermo-elasto-plastic analysis for a 1.6 kJ/mm edge weld on a carbon steel bar 12.7mm in width. Note that the displacements have been magnified by a factor of 50 to make them discemable. Note the displacements in the longitudinal direction that violate the assumptions of plane strain. |

 Опубликовано в
Опубликовано в