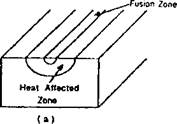
Microstructure Modeling in Heat Affected Zone (HAZ)
 21 марта, 2014
21 марта, 2014  admin
admin Many failures of welds initiate in the heat affected zone adjacent to the weld metal, e. g., in the coarse grained HAZ. For this reason, welding engineers devote much of their effort to controlling the microstructure and hence toughness of the HAZ. Metallurgists usually describe the evolution of microstructure in low alloy steels with isothermal transformation diagrams or continuous cooling transformation (CCT) diagrams. These diagrams are maps that depict the starting time and temperature of the various microstructural transformations that occur over a range of cooling trajectories. These diagrams have been developed for heat treating. Heat treating usually assumes an equilibrium microstructure at a soaking temperature of the order of 900 °С. The Jominy test, that imposes a jet of cold water on one end of a bar, is a physical model of the evolution of microstructure in heat treating.
This CCT model cannot be applied directly to welding for several reasons. The peak temperature in the HAZ of welds ranges from a bit below the eutectoid temperature to the melting point. Grain growth in the austensite phase is non-uniform in the HAZ. It is sensitive to the time and temperature curve and the presence of precipitates such as NbC that inhibit grain growth. Also the CCT diagrams are not a convenient representation for a computational model.
|
|
|
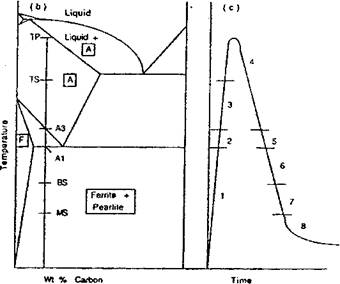
Figure 2-30: The microstructure at a point in the HAZ shown in a) under goes the thermal cycle shown in c). The microstructure evolves through the following stages: 1) ferrite and pearlite are at equilibrium; 2) ferrite and pearlite transform to austenite; 3) austenite grain growth is inhibited by NbC and VC; 4) austenite grain growth occurs; 5) austenite decomposes to ferrite; 6) austenite decomposes to pearlite; 7) austenite decomposes to bainite; 8) austenite decomposes to martensite. |
For these reasons, the model developed by Kirkaldy et al.[61] for Jominy bars, was extended by Watt et al.[66] and Henwood et al.[62] to model the HAZ of welds in low alloy steels. Input data to this model are the composition of base metal, initial microstructure and the transient temperature computed from FEM. The output is the fraction of ferrite, pearlite, austenite, bainite, martensite and the grain size of the austenite at each point (x, y,z, t).
|
The model begins by computing the Fe-C equilibrium diagram for this composition, Figure 2-30b. For each time step in the transient analysis, the phase fractions at the start are initial data and the phase fractions at the end of the step are computed. On heating, phase transformations are assumed to occur so quickly that the kinetic effects can be ignored, i. e., local equilibrium is assumed. In effect, superheating is ignored. After ferrite and pearlite have fully transformed to austenite, austenite grain growth begins after the dissolution of NbC and/or VC if they are present. Austenite grain growth is evaluated by integrating an ordinary differential equation (ODE). Grain growth continues until the A3 temperature is reached on cooling. At this time the decomposition of austensite to a) ferrite, b) pearlite and c) bainite is modeled with a sequence of ODEs. Finally, if austensite is still present at the martensite start temperature, austenite is transformed to martensite by an algebraic equation proposed by Koisten and Marburger [63]. The ODE for austenite to ferrite is shown in equation (2-19.): |
|
, X 3 (l-X)T (2-19) dt 59.6Mn + 1.45M + 67.70 + 24 AMo The exponent containing G, the austensite grain size, in the first term reflects the fact that since ferrite nucleates at the austensite grain boundary, the density of nuclei is a function of the austensite grain boundary area. The next term reflects the metal physics experiments that shows the rate of growth of ferrite increases as AT3 where AT=A3-T is the undercooling temperature for the austenite - ferrite transformation. This is due to the increasing difference in free energy between austenite and ferrite with under-cooling. The exponential term reflects the decrease in the diffusivity of carbon in iron with temperature. The denominator reflects the effect of alloying elements on diffusivity. The last term is the predator prey factor which states that the rate of production of ferrite is a product of the fraction of ferrite present, X, and the fraction of austensite present (1-Х). |
|
2 2 (AT )3 exp dX |
|
— f 23500л |
|
2(1-X) |
|
2X |
|
RT |
X = (2- 20)
’ FE
where XF is the fraction of ferrite formed and XFE is the
equilibrium amount of ferrite.
,25.4 2.
G = 1 +1.44[ln((——) x 100)] (2-21)
g
where g is the grain size in microns.
Kirkaldy has proposed the following ODE relation for the austenite decomposition to pearlite and it is similar to equation (421):
dX- 2^(A TfD f
dt 1.79+ 5.42(Cr +Mo+ 4MoM) where ДТ is the undercooling given as (Д - T) and D is a diffusion parameter and it is given by the following relation, adopted from [74]:
1 1 0.010+ 0.52Mo „
+------------ этлп---------------------- (2-23)
D, 27500 . 3700.
exp(---------- )----- exp( )
RT RT
and
X = (2-24)
PE
where Xp is the fraction of pearlite formed and XPE is the equilibrium amount of pearlite. The equilibrium value of ferrite is calculated at each time step. Therefore the equilibrium amount of ferrite at any specific temperature is the maximum amount of ferrite which can be formed from austenite. The remaining amount of austenite is available for the formation of pearlite. This allows the value of XPE to be set equal to 1 - XFE.
The ODE governing decomposition of austenite to bainite is taken from the work of Kirkaldy, adopted from Khoral [74]:
(G-1) ?7Sf)f)
d 2 2 (ДГ)2ЄХр(-^^) 2(ЬЮ 2X
=---------- 2 X 3 (1-Х)3 (2-25)
dt 10 (2.34 + 10.1C + 3.80 + 19Mo)Z
where Xis the amount of bainite formed and AT is the undercooling given as (BS-T). Z is given by the following relation:
Z = exp[X2 (1.9С + 2.5Mn + 9Ni +1.70 + 4Mo - 2.6)] (2-26)
The value of Z is set to 1.0 if: (1.9C+2.5Mn+9Ni+1.7Cr+4Mo - 2.6)<0.
The martensitic transformation is given by the following relation taken from the work of Koistenen and Marburger [63]:
XM=- exp[-*, (MS - Г)] (2- 27)
where XM is the volume fraction of martensite formed, MS is the martensite start temperature, T is the instantaneous temperature and /с, is a constant and its value for most steel types is 0.01 ГСГ1.
This microstructure model does not apply to the weld metal because the effects of solidification are ignored. Bhadeshia [64] has developed models that could be applied to weld metal.

 Опубликовано в
Опубликовано в