МЕХАНИЗМ ОЬРАЗОВ. ЧНИЯ И ДИСПЕРГИРОВАНИЯ ЛГ. ЧОМ ЕРЛТОВ ЛИСПEPCI1ЫХ I(АПОЛ11ИТЕЛЕЙ
 18 ноября, 2013
18 ноября, 2013  admin
admin Процессы сжатия смесей полимера с наполнителем в сухом со - i гоннии, происходящие в зонах загрузки и транспортировки экструзионных литьевых машин, вызывают образование характерных «он уплотнения, агломерирование дисперсных наполнителей и разрушение длинноволокнистых 110, 69|. Мри этом процесс образования агломератов зависит от формы, соотношения размеров и
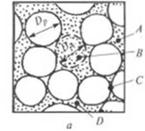
взаимного положения частиц смеси «полимер-наполнитель», концентрации компонентов, приложенного давления и соотношения размеров частиц и полостей, в которых происходит их уплотнение. Варианты взаимного расположения частиц приведены на рис. 2.40.
Если смесь состоит из гранул полимера и дисперсного наполнителя с характерными размерами, соответственно, Dp и D/, причем IL » l)f, при их сжатии образуются зоны уплотнения А, В, С (рис. 2.40, а). Последующее плавление полимера в условиях отсутствия сдвиговых деформаций в уплотненной массе приводит к образованию агломератов диаметром DA, распределенных в расплаве и движущихся с ним в рабочих каналах перерабатывающих машин. Поведение таких агломератов зависит от многих факторов. Объемное сжатие материала агломерата должно приводить к его дальнейшему уплотнению и увеличению прочности.
Разрушение агломератов в реальных условиях процессов получения и переработки может происходить по двум механизмам.
Во-первых, за счет сдвиговых напряжений т. действующих в расплаве полимера, происходит отрыв и унос отдельных частиц или их небольших образований с поверхности агломерата, что ведет к постепенному уменьшению его размеров. При этом размеры продуктов разрушения агломерата сравнимы с размерами исход-
|
|
|
|
|
|
|
|
|
г |
|
|
|
. • : |
|
• • |
|
е |
|
|
|
Рис. 2.40. Вариашы шаичного расположения чапни наполнителя и полимера 152 |
|
у//////////////// |
пых частиц наполнителя. Этот вид разрушения агломератов приводит к высокой степени диспергирования.
Пели величина развивающихся в расплаве касательных напряжений т превышает сдвиговую прочность материала агломерата хА, может происходить его разрушение за счет деформаций сдвига, причем размеры продуктов разрушения агломерата будут сравнимы с его начальными размерами.
Во-вторых, могут быть созданы условия приложения к агломерату сосредоточенных сжимающих усилий, например путем его перемещения в сужающемся канале, один из размеров которого сравним с размерами агломерата. В этом случае происходит разрушение агломерата за счет сосредоточенных сжимающих усилий, аналогичных контактным напряжениям сжатия. Как и в предыдущем случае, продукты разрушения будут иметь размеры, сравнимые с размерами агломератов, что дает низкую степень диспергирования. Таким образом, сжатие смеси гранул полимера и дисперсного наполнителя в условиях, когда размеры канала больше размеров гранул (у большинства перерабатывающих машин), приводит к образованию агломератов дисперсного наполнителя. Гру - бое их диспергирование можно осуществить созданием высоких напряжений сдвига в расплаве и продавливанием расплава через каналы, один из характерных размеров которого меньше размеров агломератов. Высокая степень диспергирования достигается за счет уноса отдельных частиц наполнителя с поверхности агломерата под действием касательных напряжений в расплаве полимера.
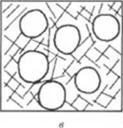
Если размеры частиц полимера и дисперсною наполнителя сравнимы, то поведение системы при сжатии и последующем плавлении полимера зависит от исходного распределения частиц (рис. 2.40, о). Первоначальное равномерное распределение частиц полимера и наполнителя исключает образование агломератов и обеспечивает высокое качество смеси после плавления полимеров. Если однородность исходной композиции недостаточна, в процессе се сжатия и последующего плавления образуются агломераты, свойства и поведение которых аналогичны описанным выше. Разброс размеров агломератов и неоднородность их распрс - 1сления в массе полимеров оказываются тесно связанными с ко - и|к])ициентом неоднородности исходной смеси.
При использовании длинноволокнистого наполнителя в смеси с гранулами полимера (рис. 2.40, в) или порошкообразным полимером (рис. 2.40, г) образуются агломераты волокнис - гого наполнителя, свойства которых определяются армирующим действием волокон, длина которых /.„ сравнима с харак - герным размером гранул полимера Дополнительным >ффектом сжатия таких смесей является разрушение волокнис - юго наполнителя |42|.
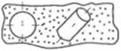
При сжатии смесей в полостях, размеры которых //сравнимы с размерами частиц полимера Dr, реальное распределение частиц полимера (рис. 2.40, ()) может быть смоделировано схемой, приведенной на рис. 2.40. е, где зоны компонента с меньшей концентрацией представлены в виде цилиндров диаметром 1)^ и высотой //. Соотношение площадей контакта полимера и наполнителя должно быть пропорционально их объемному содержанию в смеси, а равномерность распределения — коэффициенту неоднородности смеси |41|. Что касается свойств и поведения уплотненного дисперсного наполнителя, то они принципиально не отличаются от первого рассмотренного случая.
При сжатии смеси полимера и дисперсного наполнителя с размерами частиц Dp и Df, когда Dp » Df, размеры и свойства обра
зующихся агломератов определяются как содержанием отдельных компонентов, так и возможным относительным положением их частиц.
Если объемная концентрация наполнителя в смеси Справна Cof=Vf/{Vp + Yf), (2.184)
а массовая
c\f =Gf/(GP+G/)' (2.185)
(где V — объем, С — масса, а индексы «р» и «/» соответствуют полимеру и наполнителю), то плотность композиции р* будет выражаться соотношением
РА =Pp + (pf~Pp)Cof’ (2.186)
а связь между См/и Са/— уравнениями |10|
Р,/Р/
I/O,/ + Рр/Р/-1
с <У____________________ (2.187)
Со/ (|-Р/?/Р/) + Р/>/Р/
В зависимости от концентрации наполнителя образование агломератов возможно в пространстве между частицами полимера при отсутствии касания их поверхностей (зона А на рис. 2.40, а), в пространстве между соприкасающимися гранулами (зона В), на площадках контакта между гранулами (зона Q, в пространстве между гранулами, не полностью заполненном наполнителем в отсутствии сжатия (зона D) за счет арочного эффекта частиц полимера.
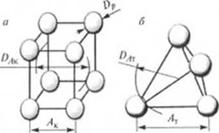
Величина агломератов, образующихся в пространстве между частицами полимера, зависит от расстояния между ними Ак и Лт (рис. 2.41, а, 6) (индексы «к» и «т* отвечают расположению частиц полимера в углах куба или тетраэдра). Для менее плотного — по углам куба — расположения частиц полимера диаметром Dp в ра-
I и 11с 110) предлагается следующее выражение для определения ветчины Ак:
|
(2.188) |
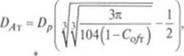
Максимальный диаметр агломератов 1)Лк, определяемый как расе гояние между поверхностями сфер двух частиц полимера, расположенных по диагонали куба (рис. 2.41, а), равен:
|
-1 |
|
(2.189) |
|
I 'К* |
|
6(|-Сс/к) 1 - Cqfk ^ ^о/к • |
Предельная концентрация Сф соответствует случаю, когда при расположении частиц полимера по углам куба происходит катите их поверхностей. Из условия Ак = Dp может быть найдена величина
С^ = 1-*/6. (2.190)
Мри меньших концентрациях наполнителя вероятнее более н ютное — по углам тетраэдра — расположение частиц полимера и тиможно образование свободного, не заполненного наполниге-
|
С/к |
и |
|
1 г Г |
У 2 у |
|
0 |
|
0.2 0.4 0.6 0.8 |
|
Рис. 2.41. К расчету размеров агломератов |
|
в 1.5 |
|
1.0 I 0.5 |
лсм, пространства между ними. Однако, поскольку частицы мелкодисперсного наполнителя образуют на поверхности частиц по j ой, способствующий их относительному смещению, при
|
|
более вероятен переход неустойчивого расположения
частиц полимера по углам куба в более устойчивое тетраэдрическое (рис. 2.41, 6).
|
|
Для тетраэдрического расположения частиц полимера (см. рис. 2.41, 6) расстояние между ними равно 110. 70|
(2.191)
а максимальный размер агломератов
|
|
|
♦ |
(2.192)
где 1 i С0ут > C0fT (здесь QyT— предельная объемная концентрация наполнителя при тетрагональном расположении частиц полимера и касании их поверхностей).
Условие А7 = Dp дает:
|
(2.193) |
Со/т =1-2727134.
С увеличением давления сжатия р происходит уменьшение С0/ вследствие того, что сжимаемость дисперсного наполнителя значительно выше сжимаемости чистого полимера. Это должно учитываться в формулах (2.190) и (2.193) введением С#{р).
Мри Со/к <С^К образование агломератов при сжатии смеси полимера и наполнителя возможно только за счет деформации частиц полимера и уменьшения расстояния между ними (А < А-,), поскольку пространство между частицами полимера не занято полностью наполнителем. Анализ этого случая может быть выполнен с использованием закономерностей деформирования двух контактирующих упругих сфер под действием контактных напряжений с учетом большой сжимаемости наполнителя, что существенно влияет на СРасстояние между центрами двух одинаковых сфер при действии силы /'изменяется на величину 5/1. равную
|
|
(2.194)
где А' = (I - v2)/(n£); v — коэффициент Пуассона; £ — модуль упругости.
В различных условиях нагружения (одноосное, плоское или объемное) мри различных упаковках системы может быть определена величина 5/1 и, следовательно, величины Сс/ и Ол путем
использования приведенной выше методики. При этом следует учитывать особенности передачи усилий частицами с различной упаковкой и определять 5/i в направлениях действия усилий нагружения F
Таксой расчет возможен для кубической упаковки при Со/ <Цу-т, для тетраэдрической — при С0у <Со/т в ограниченных пределах, поскольку формула не учитывает восприятие усилия сдавливания сфер частицами наполнителя, заполняющего пространство между ними (с увеличением 5/1 это усилие возрастает).
В случае, когда внешние усилия могут быть аппроксимированы средним значением напряжения ош, величины 5/1 и А можно получить из уравнения объемной деформации
: ic а. = (3/4)( I - vJ)/£'.C’K — число точек контакта на единицу объема, зависящее >>т типа упаковки частиц; для кубической упаковки = (3/4)/)~3; для тетраэдрической Ст 3v21)~~ ; в реальной дисперсной срсдс в процессе сжатия величина Ск изменяется, поэтому необходимо се экспериментальное определение.
Расстояние между отдельными гранулами в пределах упругого обратимого объемного деформирования определяется из уравне-
пия (2.195):
|
|
|
4 |
|
2 |
(2.196)
Следоватсльно, с помощью уравнений (2.188), (2.191) и (2.196) можно рассчитать размеры образующихся агломератов.
Необходимая информация о размерах и прочностных характеристиках агломератов реальных дисперсных систем может быть получена из зависимостей объемной деформации смеси от давления. В зависимости от концентрации C0j вид этих кривых изменяется, поскольку меняется характер сжатия областей, занятых гранулами монолитного полимера и порошкообразного наполнителя. #
В области малых концентраций наполнителя ^/<60/к И11 (см. рис. 2.41, в) сжимаемость всей системы определяется сжимаемостью каркаса гранул полимера, и, следовательно, зависимость (ЛУ/У)С от/? близка к (АУ/У) от р. При этом уплотнение наполни - I ел я происходит только в точках контакта гранул. В этих точках образуются агломераты наполнителя, размеры которых можно определить, используя решение задачи сжатия двух шаров. Диаметр
образующегося агломерата может быть принят равным диаметру круга площадки контакта двух частиц |411, сжимаемых силой Fp.:
|
l-v2 |
DA= 1,442^]FpDf
'Р—ЦГ-. (2.197)
Прочность образующихся агломератов может быть оценена по величине максимального давления на площадке контакта рк, равного
|
Ас = 0,9183/——---- т |
FnE2
(2.198)
Величина Fp для рахчичных типов упаковки частиц составляет: для кубической Л
V - р4'.
для тетраэдрической
С увеличением С0/ по мере возрастания давления в процессе сжатия включаются области, занятые наполнителем. При (рис. 2.41, в) сжимаемость всей системы определяется только поведением частиц в области дисперсного наполнителя.
По кривым сжимаемости может быть проведена оценка среднего давления в межгранульном пространстве, а следовательно, и в объеме агломерата при О/ >Q/K > а лли сильно сжимаемых смесей — при С^(р)<Сс
Для этого при заданной величине /?, находится (АУ/У)р и (АУ/У)С. Разность (АV/У), и (АУ/У)р, определяющая изменение объема смеси Д Уср = Д Урр_р + Vf. в первом приближении, может быть признана за счет сжимаемости наполнителя (АУ/У), равной 110,41]:
|
А У |
|
(2.199) |
|
VJf |
|
.mi. |
По величине этой разности по компрессионной кривой для дисперсного наполнителя находят среднее значение возникающего в нем давления /у(. С учетом найденного значения р/] во втором приближении определяют (АУ/У)^ при /?,,, = р, — /у и аналогичное значение р/, во втором приближении. Операция повторяется до достижения'требуемой точности определения.
1$ соответствии с найденным значением р/ размер агломератов наполнителя определяется по формуле:
(2•200,
I ели в смеси Dp = Df, то Д Vp и Д ^-должны определяться по со - • ннстетвующим кривым сжатия чистого полимера и наполнителя, поскольку можно считать pj' = рр = р. В этом случае
|
|
| |>л шер агломерата определяется прочностью при сжатии (отчасти наполнителя. При напряжениях сжатия менее [о]/значение />, Df. Если напряжение сжатия больше |сг|может иметь место ра (рушение как частиц полимера, так и наполнителя. В первом
• 1ч чае Da = Df, во втором происходит разрушение частиц наполни шля и заполнение межгранульного пространства полимера продуктами разрушения наполнителя, так что характерный размер II юмератов может быть рассчитан по изложенной выше методике 11И Df « Dp.
/1ля оценки размеров агломератов могут быть использованы эк - < периментальные данные по составу и структуре смеси после се
|
|
• жития в матрице и последующего извлечения и проведения дисперсионного анализа смеси. Такого рода данные являются более полными, поскольку позволяют оценить распределение размеров и юмератов, а также учитывают ряд факторов, не нашедших огра - у. женис в приведенных выше расчс - 1.14 (таких, как неравномерность распределения наполнителя, на - шчис арочного эффекта, влажность и др.).
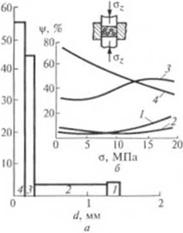
На рис. 2.42. а приведены тисни раммы распределения размеров агломератов порошкообразного мс - la. образующихся при сжатии
• меси с фанулированным поли-
Гис. 2.42. Повеление агломератов при ежа* ■ ни:
а — фракционный состав агломератов поли - п п ил низкой илотносги и мела (ог - I МПа. 0.3); 1—4 — фракции смеси; у — сожржами.■ фракции; 6 — зависимость содержания аг. то - [мюн фракций /— 4 от напряжения сжатия
этиленом низкой плотности с размерами гранул Dp х // = 3 х 5 мм и 3 х 2 мм 110]. Гистограммы показывают, что размеры агломератов меняются в широком интервале. В то же время наибольший размер находится в пределах, описываемых уравнением (2.189), что подтверждает выявленный механизм образования агломератов. Следует отметить, что в процессах переработки должна быть обеспечена требуемая степень диспергирования (3, 7| наиболее крупных образований и агломератов. В этой связи необходимо прогнозирование размеров именно этих агломератов, что и достигается использованием выражений (2.189) и (2.192).
Приведенные на рис. 2.42, б зависимости содержания отдельных фракций ог напряжения сжатия свидетельству юг о некотором увеличении доли крупных фракций, содержание которых (в м-3) равно:
а;
(2.201)
где У, = I м
С учетом необходимости проведения расчета процесса диспергирования крупных фракций, определяющих качество диспергирования, диаметр образующихся агломератов может быть найден из уравнений (2.189) и (2.192).
|
|
В качестве характерного расстояния между образующимися агломератами La может быть использован размер частиц полимера (при малых С,,/); оно может быть рассчитано но уравнению 110|:
(2.202)
Что касается дисперсии LA, то она может быть принята равной дисперсии содержания наполнителя, т. с. =о2г
Приведенные данные позволяют рассчитать размер агломератов при заданных условиях их образования, основным из которых является напряжение сжатия, что требует знания величины давления, развиваемого в смеси полимер — наполнитель на всем протяжении ее пребывания в оборудовании.
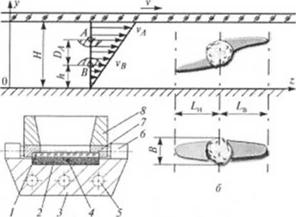
Экспериментальное изучение поведения агломератов наполнителя в условиях сдвиговых деформаций было проведено в устройстве, показанном на рис. 2.43, а |41|. Условия простого сдвига расплава 2 создавались путем перемещения с заданной скоростью верхней подвижной плиты /относительно нижней неподвижной 3. Частицы уплотненного под контролируемым давлением наполнителя 4 диаметром 1)л (рис. 2.43, б) помещались в расплав толщиной // на определенном расстоянии Л от нижней плиты. В процессе перемещения вдоль оси z верхней плиты через выполненную в ней прозрачную стенку / фиксировалась картина деформации аг-
|
Рис. 2.43. К механизму лиспсршровання агломератов наполнителя: а - устройство для исслелования диспергирования агломератов при простом сдвиге; б - картина диспергирования агломератов |
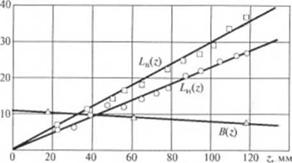
юмерата, длины следов на уровне верхней /.„ и нижней границ частицы, ее ширина В, а после охлаждения производился анализ распределения размеров частиц в различных частях следа 110|. Необходимый температурный режим поддерживался системой регулирования температуры 5 (см. рис. 2.43, а), фиксированная величина // — роликами 6, а гарантированное поджатие расплава — ipvioM 8. Пример результатов измерения Ln(z), L„(z), B(z) приведи на рис. 2.44. Кривая распределения размеров частиц, полученных в результате разрушения агломерата порошкообразного мела
|
L, В. мм
Рис. 2.44. Перемещения характерных точек в зависимости от пути диспергирования (см. рис. 2.43, 6) |
при сдвиге расплава поли этилена низкой плотности при температуре 453 К, скорости v = 0,24 м/с, расстоянии между пластинками // = 4 мм и первоначальном диаметре агломерата Da = 2 мм, приведена на рис. 2.45.
|
Гис. 2.45. Пример кривой распределения размеров частиц в продукте разрушения агломератов. Композиция - поли пилен высокого давления + мел» |
Г1 роведе иные автора ми работ 110, 71, 72| исследования позволили сделать следующие выводы.
А. Характер разрушения а гломерата оы редел ястся
соотношением величин действующих в расплаве касательных напряжений на поверхности агломерата хшЛ и его прочностных характеристик, зависящих от степени уплотнения при сжатии дисперсного наполнителя в момент образования агломерата, прочности материала агломерата при сдвиге и предельных касательных напряжений на поверхности, вызывающих отрыв отдельных частиц агломератов хтА. При этом возможны следующие четыре случая (очевидно, что хА > |т„.д|).
1. При 0 < хл < |thvJ] разрушения агломератов не происходит, и они перемещаются в расплаве, совершая вращательное движение с угловой скоростью ыА, равной скорости сдвига у.
2. При |тм| < xwA < ItJ преобладающим механизмом разрушения агломерата является отрыв отдельных монолитных частиц наполнителя или небольших агломератов с поверхности и унос их движущимся расплавом. При этом виде разрушения агломерата наблюдается тонкое диспергирование частиц; средний размер уносимых частиц «полимер—наполнитель» может быть принят равным исходному среднему размеру частиц дисперсного наполнителя /)/, а для сильно ai ретирующихся наполнителей — уточнен экспериментально.
3. При xwA > |тд| наблюдается разрушение в массе агломерата за счет сдвиговых деформаций в уплотненном наполнителе. При этом образуются достаточно крупные фрагменты агломератов (см. рис. 2.45), а также происходит унос отдельных частиц дисперсного наполнителя с поверхности агломератов, что дает широкий спектр размеров продуктов разрушения.
4. Особым случаем является процесс диспергирования агломератов наполнителя, образовавшихся путем обволакивания расплавом полимера неуплотненного наполнителя. При этом деформирование агломерата аналогично деформированию при сдвиге кап-
iii песмешивающсйся жидкости, причем в объеме дисперсного исполнителя происходит «перекатывание» отдельных частиц, а гакже их переход с поверхности агломерата в расплав.
1>. Наиболее интенсивное разрушение агломерата происходит в ючках, в которых нормали к поверхности агломерата перпендикулярны направлению сдвига (точки А и Н на рис. 2.43, б). В этих ючках направление действия касательных напряжений совпадает с направлением наименьшего сопротивления уносу частиц наполни юля с поверхности агломерата.
В. Разрушение агломерата происходит в процессе его вращения, вследствие чего зоны интенсивного уноса частиц наполнителя с поверхности агломерата (вблизи точек А и В на рис. 2.43, в) последовательно охватывают практически всю его поверхность.
I Размер в направлении сдвига следов разрушения агломерата соответствует величинам линейных перемещений его точек, прилежащих к стенкам канала. Ширина агломерата меняется значи - юльно меньше (см. рис. 2.43, б).
11ри анализе процесса диспергирования агломерата диспсрсно - ю наполнителя за счет отрыва частиц с его поверхности под дей - < гвием касательных напряжений в движущемся расплаве необходимо рассмотреть кинетику процесса, динамику образования сле-
i. i продуктов диспергирования, его размеры и состав.
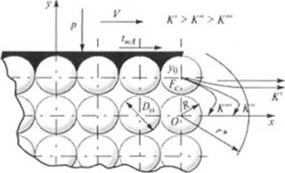
Интенсивность отрыва отдельных частиц наполнителя с поверхности агломерата (рис. 2.46) определяется рядом факторов, основными из которых являются: соотношение между касательными напряжениями на поверхности агломерата xwA и силами связи между частицами Fc; ориентация поверхности агломерата относи - к'льно направления действия касательных напряжений; величина ■ынления в расплаве р; смачиваемость материала наполнителя расплавом полимера.
|
Рис. 2.46. К анализу уноса части наполнителя с поверхности агломерата |
Процесс отрыва и уноса частиц наполнителя в случае смачиваемости материала наполнителя расплавом полимера можно моделировать следующим образом |2|: расплав, имеющий температуру Г, вязкость ц и находящийся под давлением р, вблизи поверхности агломерата движется со скоростью v при скорости сдвига Унд» что создает на его поверхности касательные напряжения xwA. Отрыв частицы наполнителя с поверхности агломерата возможен только после пропитки расплавом слоя агломерата толщиной, равной диаметру частиц наполнителя, после чего унос - частиц происходит по механизму, предложенному в работе |4) (см. рис. 2.39, а). При этом время уноса частицы наполнителя с поверхности агломерата /у равно сумме времени пропитки /,,р слоя наполнителя толщиной D„ расплавом полимера под давлением р и времени перемещения оторванной частицы /„ на расстояние г*, на котором сила связи частицы с агломератом Fc пренебрежимо мала |4|.
Время пропитки /|ф может быть рассчитано с использованием нескольких подходов.
При большом давлении расплава время пропитки можно определить по скорости пропитки (1>пр (см. рис. 2.46):
|
|
(2.203)
где Ка — константа скорости пропитки; ц — вязкость расплава полимера.
Градиент давления dp/dy можно принять равным p/D„ |10|, если в процессе диспергирования агломерата создаются условия для удавления воздушных включений. В противном случае следует рассмотреть изменения давления воздуха в пространстве между частицами в агломерате. Время пропитки /ир составит:
|
(2.204) |
КаР
Методика расчета скоростей пропитки (фильтрации) расплав;! через поры между гранулами при октаэдрической и гексагональной упаковках приведена в работе |42|.
Время пропитки с учетом смачиваемости частиц наполнителя рассчитывается по формуле 110]:
где — константа скорости смачивания |42|; Р — статический угод смачивания; о — поверхностное натяжение; Ь — эмпирическая константа.
|
|
|
Время перемещения частицы равно: |
|
| .!>• »■, i,.<, — скорость расплава вблизи поверхности агломерата. |
|
•и шчнны критического радиуса разделения г*. Критический радиус разделения г* . пи ши с параметром К (рис. 2.46) отношением сил, стремящихся оторвать части - in. к силам связи частицы в агломерате. |
|
(2.206) |
|
которая зависит от |
11о аналогии с 110| в данном случае величина К равна:
|
(2.207) |
АГ=3 kDa[xwA]/Fc.
Величины г* и Fc могут быть определены по напряжениям xwA и перемещениям Ду, соответствующим концу участка упругих деформаций при испытаниях уплотненных сыпучих сред на сдвиг 11-11. причем Fc определяется по формуле:
|
(2.208) |
^ - ЧАI ^т. к *
1 Ч* — число точек контакта между частицами наполнителя на единице плотни плоскости сдвига; Ntx = l/DA: /— единица измерения DA.
Поскольку унос одной частицы осуществляется за время /в с поверхности DAr*, скорость процесса уноса частиц с поверхности. и ломерата (число частиц с единицы поверхности за единицу времени) составляет: ,
|
|
|
(2.209) |
|
|
|
и ic PY — удельная мощность, рассеиваемая в расплаве вблизи поверхности агломерата), то |
|
(2.210) |
|
Гак как |
|
|
|
или Ny = KTwA |
(2.211)
|
|
|
< А| и К2 — коэффициенты, зависящие от размеров агломератов наполнителя и ни ikocth расплава. |
|
(2.212) |
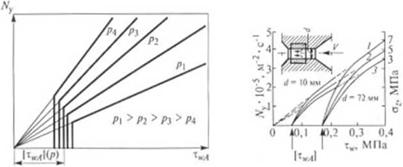
Очевидно, что полученные уравнения действительны при *wa > IVil* Графически зависимость Ny = J{xwA. р) при различных давлениях образования агломератов имеет вид прямых, проходящих через начало координат и ограниченных слева абсциссой %л = КЛ (Р“с. 2.47).
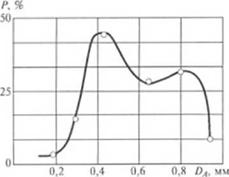
Экспериментальная проверка полученных соотношений, выполненная путем продавливания расплава через канал, стенки которого образованы уплотненным при фиксированном давлении р дисперсным наполнителем, с последующим анализом расплава на выходе из капилляра, подтвердила характер кривых |41|:
Ny=f(xwA. p),
однако в области xwA *= |tKViI наблюдается плавное изменение Ny в зависимости от xW/i (см. рис. 2.48).
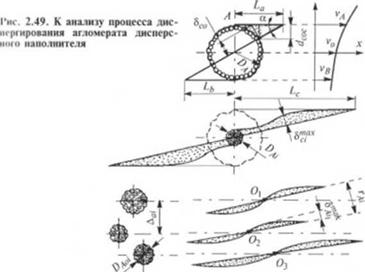
В процессе разрушения агломерата за счет отрыва частиц с его поверхности образуются два диаметрально расположенных следа длиной Л = La = Lb (рис. 2.49), определяемой соотношением 10,41): л.
L = !fr, (2.213)
где Г — деформация сдвига, расчет которой изложен в следующем разделе.
Изменение диаметра агломерата во времени описывается уравнением:
= (2.214)
|
где А'( — лап я поверхности агломерата, с которой одновременно осуществляется унос частиц (A'j = 0,5); и р„ — плотность агломерата и монолитною наполнителя соответственно. |
|
Рис. 2.47. Теоретическая - зависимость Л'у от хыЛ |
|
|
Р т
Рис. 2.48. Зависимость интенсивности уноса Nf частиц наполнителя с поверхности агломерата (полиэтилен ниткой ILTO111 ости + мел) от величины т». Значения р:
I - 7 МПа; 2-5 МПа; 3—3 МПа
|
|
Толщина следа 5„, в интервале деформаций сдвига 0 < Г<, Гк(Гк — « и»иг, при котором Г)А —> 0) находится из уравнения (10]
(2-2.5)
.1 юл щи на частиц следа 5W в направлении, перпендикулярном направлению сдвига, определяется по формуле:
бсос^соГ^^р. (2.216)
В процессе деформации сдвига и уменьшения диаметра агломерата создается след, профиль которого имеет максимальную юлщину &J! Jax при L = LJ2 (рис. 2.49), соответствующую некоторому сдвигу /тах. а вся система исходных агломератов с расстояниями между центрами /•„,,(/ = 1.2,3, 4) по достижении Г = 1 преобразуется в полосы, параллельные друг другу и направлению
» iHiira и отстоящие друг от друга на расстояние гм.
Объемная концентрация наполнителя в этих полосах равна:
с„/=6 Р .
(«Г) DaF^ (2-217)
. и - Ga - масса агломерата.
В дальнейшем процесс сдвига среды сопровождается изменением толщины полос в соответствии с теорией ламинарного смешения 1111:
Гл=ГГп ’ <2-218>
со/7 В2
где Г — обобщенная деформация сдвига; hi » Mi — вязкость расплава полимера и композиций соответственно.
Величина / равна (111:
1
1+ +уХ+у2*)’ (2.219)
где v - коэффициент Пуассона; - компоненты тензора деформации.
Таким образом, в случае деформации расплава, содержащего агломераты наполнителя, для достижения требуемого качества диспергирования и смешения, определяемого максимально допустимой толщиной полос |rmax], требуется приложение суммарной величины сдвига Г, равной:
Г=Гк + Гг, (2.220)
где Гк — сдвиг, необходимый для разрушения агломерата; Г, — сдвиг, необходимый для изменения толщины полос до (r^J.
В связи с этим анализ процесса диспергирования агломератов сводится к нахождению величины сдвига в перерабатываемом материале, для чего требуется знание распределения скоростей частиц, напряжений и времен пребывания материала в зоне деформирования. Эти вопросы рассмотрены в последующих разделах данной главы.



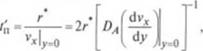
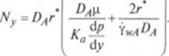
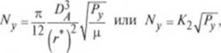
 Опубликовано в
Опубликовано в