Дисперсный состав пен представляет теоретический и прак­тический интерес. Удельная поверхность раздела в барботажных аппаратах, характеризующая интенсивность различных процес­сов, дисперсность пен в аэрозольных упаковках, микрострукту­ра пен, образующихся при приготовлении мороженого, конди­терских изделий, а также вспененных пластмасс, в первую оче­редь интересуют производственников, так как от дисперсного состава зависит качество продуктов и экономические показате­ли технологических процессов.

Дисперсность пеп определяют микрофотографированием, ме­тодом ослабления светового потока, методом Б. В. Деригина

И др.

Основным методом определения дисперсности пен является метод микрофотографирования [191]. Установка для микрофо­тографирования состоит из мпкрофотонасадкн с фотоаппара­Том, предметного столика, обеспечивающего перемещение кюве­ты с пеной в вертикальной плоскости, подставки для прибора, а также осветителей. Фотографирование можно проводить и отраженном пли проходящем свете. Общее увеличение должно составлять 30—100 раз.

Для определения дисперсности пен методом микрофотогра­фирования пены иногда предварительно замораживают. В каче­стве охлаждающего агента используют жидкий азот. Кювету с пеной помещают на медную платформу, которая сообщена с сосудом, содержащим жидкий азот, с помощью медного стержня, являющегося проводником холода. Платформу для размещения кюветы с пеной располагают внутри сосуда Дыоа - ра на расстоянии нескольких сантиметров над уровнем жидко­го азота. Пена замерзает за 2—3 с, что особенно важно при изучении нестабильных пен.

Фотоснимки пен обрабатывают следующим образом. Все пузырьки разбивают на фракции но размерам (в мкм) 0- т, т—2т, 2т—3m и т. д. С помощью специальной шкалы, изго­товленной с учетом увеличения, подсчитывают на фотоснимках число пузырьков различных фракций. Пузырьки каждой фрак­ции характеризуют средним диаметром D : т/2, Зт/2, 5т/2 (мкм) и т. д. На основании этих данных составляют таблицы распределения пузырьков но размерам N(d), по поверхности S(D) и по обьемам V{D)

Ni = nij^ni; Si^dfntjy^df-n,; V,- = dfn, j V df,^ (5.4)

Где 7i( — число пузырьков фракции i с диаметром 'V, "Zrii — общее число пу­зырьков всех фракций; Ni, Si и Vi — частичная концентрация, поверхность и Объем пузырьков фракции i.

С помощью таких таблиц можно вычислить средний диа­метр, средний объем и среднюю поверхность пузырька:

_ _ к - 2D|W|

2>. 2*. V'

9?

Можно также определить следующие характеристики пены: среднюю удельную поверхность раздела раствор — воздух, при­ходящуюся на единицу объема_ раствора, в пене, имеющей оди­наковые пузырьки диаметром d: | _ S (D«) Vr 6 Vr 6 „

7—952
И истинную удельную поверхность раздела раствор — воздух в пене, приходящуюся на единицу объема пены:

^Sjdf) Nt yr 6Vr^dfN, 6(P-I)2<VW,-

"ж DfWj 2 dfNi

Где р — кратность пены.

По имеющимся данным можно также рассчитать AS/S — до­лю истинной удельной поверхности пены, приходящуюся на пу­зырьки различных фракций.

Точность метода микрофотографирования зависит от числа подсчитанных пузырьков в каждой фракции размеров. Поэтому самые представительные фракции определяются с наибольшей точностью.

Для оценки точности определения дисперсного состава пен методом мик­рофотографирования проводили трехкратное фотографирование трех проб пены (9 фотографий). На каждой фотографии подсчитывали 200—300 пузырь­ков. Учитывали только те фракции, удельный вес которых в общем числе пу­зырьков составлял не менее 16% всех пузырьков. Таких представительных фракций было три, причем каждая фракция в среднем охватывала по 22% всех подсчитанных пузырьков (всего 66% пузырьков). Остальные в расчет не принимались.

Среднее квадратичное отклонение сг и доверительные интервалы средней арифметической /э5 и /99 рассчитывали но уравнениям:

Где Xi и х — среднее число частиц в опыте и приходящихся на одну фракцию в опыте; п — число измерений; T — критерий Стьюдента.

При трех измерениях /а5= ±6, а /аэ=±14, т. е. с вероятностью 0,95 пре­дельные отклонения от средней арифметической не должны прегышать 6/22-100= ±27%, а с вероятностью 0,99 — должны составлять ± 64%. Эти данные показывают, что точность измерений при использовании только трех фотографий невелика.

Для сравнения были проведены аналогичные расчеты для определения точности дисперсионного анализа эмульсии молока. С этой целью использова­ны данные из работы [192]. Как и при изучении пеп, учитывали только наи­более представительные классы (фракции) размеров капель эмульсии молока, каждая из которых включала не менее 18%, а все четыре наиболее предста­вительные фракции — 80% капель эмульсии молока. Так как в этой работе приведены данные для девяти одинаковых проб молока, можно рассчитать величины а и /95 (/9S) по экспериментальным данным, полученным при обра­ботке трех, шести и девяти снимков (общее число сосчитанных шариков со­ставляло 2824). Полученные результаты представлены в табл. 6.

(5.7)

Эти данные свидетельствуют о практически равной точности дисперсион­ного анализа эмульсии и пены при использовании для расчетов одинакового числа снимков. Вместе с тем можно видеть, что увеличение числа подсчитан­ных частиц до 2000 вызывает резкое сужение доверительного интервала, то­гда как дальнейшее возрастание числа подсчитанных частиц оказывает су­щественно меньше влияния. Поэтому для представительных фракций размеров пузырьков подсчет 400 частиц в опыте является, по-видимому, оптимальным. Данное обстоятельство, однако, нельзя распространять на менее представи­тельные фракции, поскольку точность полученных результатов в этом случае значительно ниже.

Таблица 6. Точность анализа дисперсного состава эмульсий и пен методом микрофотографирования Объект Число снимков Число опытов Среднее Число Среднеес чис­ло части:",, приходя­щихся на од­ну фракцию в опыте Среднее (квадратич­ное откло­нение Доверитель­ные интер­валы Частиц в опыте /»5 / 89 Молоко Пена 3 6 9 3 3 3 1 3 940 1880 2820 700 185 375 560 155 2,0 1,8 1,8 2,4 5,0 1,9 1,4 6,0 12,0 3,0 2,0 14,0

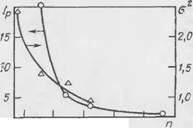
Для подтверждения этих данных по результатам опытов, представленных на рис. 16, по уравнению (5.4) рассчитаны доверительные интервалы для из­мерении с 2, 3, 4 и 8 фотоснимками (на каждом снимке — около 400 частиц). Полученные значения доверительных интервалов для трех наиболее предста­вительных классов (около 70% всех частиц) в зависимости от числа подсчи­танных часпщ, а также средине квадратичные отклонения а2 полученных рас­пределении изображены па рис. 44. Из представленных кривых следует, что 1200—1600 частиц в опыте является пределом и дальнейшее увеличение чис­ла измеряемых частиц при дисперсном анализе эмульсий и пен нерациональ­но, т;п? кик тчпость анализа при этом увеличивается незначительно.

Учтивая значительный разброс дпамсфов пузырьков в пенал, л иные, полученные при измерении 100—200 и менее пузырьков, необходимо рас­сматривать лишь как ориентировочные. Следует иметь в виду также то, что в процессе старения пены одновременно изменяется и форма пузырьков.

Метод определения дисперсности пены, путем микрофотогра­фирования прост в реализации, однако большая трудоемкость ограничивает его применение. Поэтому его обычно используют для калибровки приборов, применяемых в более простых мето­дах.

Кларком н Блэкманом была обнаружена линейная зависи­мость между коэффициентом ослабления света пеной и ее удельной поверхностью Syn. Дальнейшие исследования стабиль­ных и нестабильных пен [193] подтвердили наличие зависимо­сти между этими параметрами:

5уд=Л(/о//-1) (5.8)

500 1000 1500 2000

7*

Аа

Где K — коэффициент пропорциональности, 10 и / — интенсивность падающего и прошедшего через пену света соответственно.

Рис. 44. Изменение доверительного ин­тервала /р и среднего квадратическогс отклонения аг для доверительной ве­роятности 0,95 в зависимости от числа сосчитанных пузырьков.

Линейность функции 5=/(/0//) может быть использована для быстрого определения удельной поверхности раствор — воз­дух в пенах [194].

По мере старения пены ее оптические свойства существен­но изменяются, и она становится более прозрачной. Процесс изменения удельной поверхности пены описывается уравнением

Где S"УД и 5УЯ — удельная поверхность неиы в момент т=0 и т соответствен­но; а — постоянная.

Однако вряд ли будет справедливым полагать, что все без исключения пены распадаются в соответствии с такой простой зависимостью. Она справедлива лишь для некоторых частных случаев. По-видимому, это обусловлено соотношением скоростей трех известных процессов разрушения пены. Так, для очень стабильных пен изменение поверхности раздела во времени, пропорциональное коэффициенту ослабления света, можно опи­сать двумя экспонентами. При этом на начальной стадии рас­пада пены уменьшение коэффициента ослабления происходит более интенсивно, чем на второй стадии [2]. Это объясняется, очевидно, преобладанием истечения жидкости из пленок на пер­вой стадии разрушения пены, а на второй — другими факто­рами разрушения пен.

Для определения поверхности раздела раствор — воздух в пене методом ослабления света можно использовать прибор с фотоэлектрическим интегратором и фотоэлементом, на который падает свет после прохождения через слой пены. Ток фотоэле­мента усиливается и регистрируется гальванометром. Оптиче­ский прибор, который можно применять для измерения меж­фазной поверхности эмульсий и пен, описан в работе [195]. По­верхность раздела рассчитывают по уравнению (5.8), коэффици­ент K определяют экспериментально путем сравнения с систе­мой, имеющей известную межфазную поверхность.

Оптический метод используют также для определения удель­ной поверхности раздела движущейся по трубопроводу пены.

Для определения поверхности раздела можно использовать методику и прибор Б. В. Дерягина, разработанные им для изу­чения механических свойств пен. Пену помещают в сосуд, где ее для разрушения сжимают платформой. Избыточное давление газа, выделившегося при разрушении пузырьков пены, фиксиру­ют манометром, по показаниям которого с учетом измеренного объема разрушенной пены вычисляют избыточное давление Др, связанное с удельной поверхностью пены соотношением (2.12). Так как по определению SyA=S/V, то после подстановки значе­ний поверхности S и объема V пены получаем SyA=3/r. Радиус пузырька можно определить по уравнению (1.5), тогда оконча­тельно получим:

5уД = ЗД/?/(2ст) (5.10)

Разработан метод определения дисперсности пен путем из­мерения их кратности и давления в каналах Плато [196]. Ме­тод основан на использовании зависимости

« = (0,46 — 1,8) а/Ар (5.11)

Где а — длина ребра додекаэдра, Др — разность давлении в каналах Плато при высоте сголба пены /i=0 Ii h=h.

Экспериментальная проверка метода показала удовлетвори­тельную сходимость е расчетом по уравнению [197]:

С = 0,95 У га/р (5.12)

Где г — радиус пор фильтра; р — плотность раствора пенообразователи.

Метод применим только для исследования полиэдрических «сухих» пен.

Авторами работы [198] предложен метод определения удельной поверхности пен с использованием ультразвуковых ко­лебаний. В интервале концентраций 0,5—5% и частот колеба­ний 0,5—1 МГц коэффициент потерь ультразвука а не зависит от природы и концентрации ПАВ, а зависит только от дисперс­ности пены. Принцип метода заключается в измерении коэффи­циента а при частоте 0,5 или 1 МГц, который связан со сред­ним диаметром пузырьков уравнением

А — 1/(1/а0 + B/Dj (5.13)

Где а0 — коэффициент потерь ультразвука в воздухе при данной частоте; Fi—const (Я=— 0,48 см2 прн 0,5 МГц и б = —4,20 см2 при 1 МГц).

Следует отметить, что метод применим для «стекших» пен с диаметром пузырьков в пределах 1—3 мм.

Радиографический метод анализа дисперсности пен основан на свойстве р-частиц, рентгеновского и у-излучений не оказы­вать разрушающего действия на мыльные пленки (в отличие от а-частиц) [199]. Согласно этому методу пену, помещенную в сосуд, облучают рентгеновским или у-излучением (можно ис­пользовать также жесткое р-излучение); излучение, прошедшее через сосуд с пеной, действует на рентгеновскую пленку. Полу­ченные после проявления радиографические снимки используют для определения площади межфазной поверхности. Для полу­чения более контрастного изображения в раствор добавляют солн, содержащие тяжелые элементы (барий, бром, иод и др.).

Радиографический метод не нашел покт практического при­менения.

Для определения поверхности раздела в барботажном слое чаще всего применяют метод фотографирования [200] и метод, основанный на отражении светового потока от поверхности слоя пены [201]. Статистическая обработка снимков в методе фото­графирования основана на том вероятностном факте, что если бесконечная линия многократно и произвольно накладывается на замкнутую плоскую фигуру, то средняя линия отрезка I, пе­ресекающая эту фигуру, равна

L = nS/ П (5.14)

Где S и Г1 — площадь и периметр плоской фигуры.

Для линий конечной длины I получено другое выражение [202]:

NS/П = nl/c (5.15)

Где п— число попаданий всего отрезка внутрь плоской фигуры; с — число пересечений отрезка с периметром фигуры.

Поскольку расположение линий на плоской фигуре формаль­но эквивалентно произвольному размещению плоскости в трех­мерном пространстве, для последнего случая выведено соотно­шение [201]

Nf/C-4 Vyt| VS| (5.16)

Выразив величины Vi и S< через диаметр пузырька D и подста­вив их в уравнение (5.16), получим:

СГ= Зп1/(2с) (5.17)

Для нахождения величин, входящих в уравнение (5.17), на фотоснимки пены в барботажном аппарате произвольно и мно­гократно накладывают сетку, состоящую из большого числа ли­ний известной и постоянной длины, и таким образом находят значения п и с.

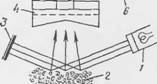
При определении поверхности раздела методом, основанным на отражении светового потока, количество световой энергии, накапливающейся за время т, фиксируют с помощью интегра­тора (рис. 45). Последний по достижении необходимого заряда дает импульс, регистрируемый электромеханическим счетчиком. Коэффициент отражения света от поверхностей вычисляют по уравнению

Я = ///ст (5.18)

Где I и /ст — интенсивность отраженного света от реальной и стандартной (молочное стекло) поверхностей.

Удельную поверхность контакта фаз рассчитывают с по­мощью калибровочного графика, построенного для стеклянных шариков различных диаметров, в соответствии с уравнением

(/?.//?) -1=/(1/5уд) (5-19)

Где Roc = СМ — коэффициент отражения света при бесконечно большой поверх­ности; С — коэффициент пропорциональности; М=Цп'1п")г — l]/[(n'/n")2+1]; П' и п" — показатели преломления для дисперсной и сплошной сред соответ­ственно.

Размеры пузырьков пен, образующихся при барботнрова- нии, можно измерять с помощью зонда, представляющего собой вертикальную стеклянную трубку [203]. По разные стороны

P—F*

§

(8)

Регистра Регистра

О

_ Регистрация

О

О

Рис 45. Схема прибора для определения поверхности контакта фаз метолом

Отражения света [51]:

/ — неючпнк снега; 2 — газожндкостныП слоА; 3— зеркало; 4— (]нт)1л>1||н>гнн.'ич|н1'; 5 _ интегратор; 6 — электромеханический счетчик.

Рис. 46. Схема, поясняющая принцип работы фотоэлектрического счетчика пу­зырьков [203].

Зонда размещают осветительную лампу и фотоэлемент (рис. 46). Пузырьки воздуха, попадающие в зонд, подсчитыва­ют с помощью фотоэлемента, а самописец регистрирует время прохождения каждого пузырька. Если прибор отградуировать по пузырькам известного объема, то по времени прохождения пузырька можно определить его объем или диаметр.

Из других современных методов определения поверхности контакта фаз в барботажном слое следует отметить метод, ос­нованный на просвечивании у_излУчением [204], позволяющий регистрировать характер распределения газа по высоте и по ссчепию столба пены в аппарате.