Метод построения факторно-стоимостных математических моделей
 4 ноября, 2011
4 ноября, 2011  admin
admin Наиболее эффективным способом организации массовой оценки является создание комбинированных факторно-стоимостных моделей, которые отражают зависимость рыночной стоимости машины от ее основных эксплуатационных параметров, выполняющих роль ценообразующих факторов. Расчет стоимости с помощью моделей значительно ускоряет процесс оценки в сравнении с обычной практикой «поштучного» сравнения оцениваемых объектов с их аналогами. Ведь одна математическая модель может быть применена к большой группе машин одного класса, а, кроме того, оценка легко автоматизируется благодаря применению компьютерных технологий.
При разработке математической модели для массовой оценки возникает необходимость отобрать небольшое количество ценообразующих факторов, однозначно определяющих величину рыночной стоимости. Из множества разнообразных технических параметров нужно выбрать такие, которые представляют ценность для потребителя. Только отбор параметров с позиций по-лезностного подхода позволяет получить математическую модель, дающую в результате стоимость замещения, а следовательно, применить сравнительный подход при оценке.
Первичным критерием отбора ценообразующих параметров-факторов служит триада факторов: «назначение» - «качество» -«производительность». Факторы характеризуются техническими параметрами. Причем один параметр может одновременно характеризовать объект с нескольких позиций, т. е. брать на себя функцию не одного, а нескольких указанных факторов. Например, у прессов номинальное усилие свидетельствует как об области применения, так в определенной степени и об их производительности.
Отбираемые для построения математической модели параметры могут быть подразделены на три уровня с точки зрения значимости факторов.
К первому уровню относятся те параметры, которые характеризуют фактор «назначение». Например, у технологических обрабатывающих станков к параметрам первого уровня относятся размеры изготовляемой или обрабатываемой заготовки, у гильотинных ножниц это толщина и ширина разрезаемого листа, у нагревательной печи — размеры рабочей камеры и т. п. Качественный состав параметров назначения служит часто ограничителем объема множества однородных объектов.
Второму уровню соответствуют параметры, характеризующие факторы «производительность» и «качество», в отношении которых у разных видов машин и оборудования разная степень предпочтения. Например, для технологических машин на заключительных операциях обработки первое место принадлежит фактору «точность» или «качество», а для технологических машин на начальных операциях превалирующую роль играет фактор «производительность». Отбор факторов второго уровня должен учитывать состав образуемой группировки объектов. Так, если в нее попадают объекты примерно с одинаковым качеством функционирования, то нет необходимости отбирать для модели параметры этого фактора.
Третий уровень образуют параметры, характеризующие фактор «конструктивные особенности и наличие дооснащения». Аналоги, включаемые в группировку, могут быть объединены в отдельные подгруппы по таким признакам, как наличие средств автоматики, дополнительных устройств, применение особого схемного решения и т. п. Эти параметры должны быть также
Включены в математическую модель. Кстати, учет параметров третьего уровня расширяет сферу использования математической модели, позволяет применять ее к большим группировкам объектов.
Следует подчеркнуть, что создаваемая для целей массовой оценки модель должна распространяться на возможно большую по численности группировку аналогичных объектов. Поэтому отбор влияющих параметров-факторов и формирование группировки объектов должны выполняться параллельно.
Созданию небольшого числа широкоуниверсальных моделей, применимых к большим группировкам объектов (что, кстати, хотелось бы получить), препятствуют два ограничения: во-первых, функциональная, а следовательно, и полезностная неоднородность объектов и, во-вторых, наличие оригинальных объектов в виде специальных машин и машин-гибридов, которые затруднительно отнести к какой-либо известной группировке.
Анализ опыта массовой оценки показал, что для ее целей наиболее подходят гибридные математические модели мультипликативной формы, их структура включает две части: базисную и надстроечную: базисная представляет собой корреляционно-регрессионную модель факторов полезности, с помощью которой рассчитывается полная стоимость замещения (восстановительная стоимость); надстроечная включает комбинированную модель для расчета коэффициента, учитывающего фактор физического износа.
Мультипликативная форма гибридной модели предпочтительнее аддитивной формы благодаря лучшему отражению интегрированного влияния всех факторов на конечный результат, возможности использования более универсальных, нелинейных зависимостей и более легкой корректировке на предмет актуализации.
Построение корреляционно-регрессионной модели ценооб-разующих факторов полезности лучше всего выполнять на основе степенной функции, преимущество которой заключается в том, что она дает описание нелинейной связи (в широком диапазоне связь между стоимостью и факторами именно нелинейная), весьма наглядна, логически объяснима и легко приводится к линейной форме методом логарифмирования (что открывает возможность применения регрессионного анализа).
Однако модель степенной функции в чистом виде обладает тем недостатком, что она применима для случая, когда влияющие параметры являются непрерывными переменными. В то же время у машин и оборудования имеются и дискретные параметры, и характеристики, для учета влияния которых применяют гибридную модель следующего вида:
У-аохх{ хх2 х...ххп хоп+{ хоп+2 х...хоп+кл,
Где У — искомое значение полной стоимости замещения;
Х|, х2, ..., Хя — Влияющие на стоимость технические параметры; AQ, #|, A2, ..., Ап — параметры математической модели; Ьц+1, Bn+2, ..., Bn+K — Значения дискретных параметров-коэффициентов; jc/;+1, х/7+2, ..., Х„+к — Бинарные переменные (0 или I);
К — количество дискретных параметров-коэффициентов.
Методика разработки корреляционно-регрессионных моделей описана в гл. 4, поэтому не будем на ней останавливаться. Особого внимания заслуживает процедура преобразования качественных характеристик в цифровые значения коэффициентов. При этом дискретные качественные характеристики разбиваются на категории и для каждой определяется ее «цена» в виде корректирующих коэффициентов.
Рассмотрим метод, позволяющий оптимизировать значения корректирующих коэффициентов, характеризующих силу воздействия разных категорий качественных характеристик на оцениваемую стоимость. Метод реализуется в рамках корреляционно-регрессионного моделирования.
Покажем применение этого метода на примере. Задача заключается в том, чтобы разработать корреляционно-регрессионную модель для расчета полной стоимости замещения листогибочных машин. Роль фактора «назначение» была поручена двум размерным параметрам: наибольшая толщина и наибольшая ширина сгибаемого листа. Факторы «производительность» и «качество» не учитывались, поскольку в рассматриваемой совокупности машин не наблюдалось существенного различия. Фактор «конструктивные особенности» проявляется в виде машин: с поворотной балкой и трехвалковые. Два первых параметра являются непрерывными величинами и измеряются в натуральных единицах. Третий параметр — вид машины — качественная дискретная характеристика, которую предстоит учесть с помощью соответствующего корректирующего коэффициента.
В начале 2003 г. на первичном рынке оборудования в Москве и Санкт-Петербурге ведущими станкоторговыми компаниями продавались новые листогибочные машины 10 моделей. Данные о ценах (включая НДС) и технические параметры представлены в табл. 5.1.
Чтобы учесть в создаваемой математической модели влияние фактора конструктивных особенностей, реальные цены машин были заменены на приведенные. Приведенная цена - это условная цена, которую могла бы иметь та или иная машина, если бы она соответствовала базовому виду (в нашем примере таким видом выступает машина с поворотной балкой):
![]()
Где Ц — реальная цена машины; Цпр — приведенная цена машины; Кв — коэффициент вида машины.
Таблица 5.1 Исходные данные о ценах и технических параметрах листогибочных машин
|
Наиболь - |
Наиболь - |
Цена |
Приве - |
||
|
Модель |
Шая тол - |
Шая ши - |
Тыс. |
Вид машины |
Денная |
|
Щина лис - |
Рина лис - |
Руб. |
Цена, |
||
|
Та, мм |
Та, мм |
Тыс. руб. |
|||
|
ИВ2146 |
3,5 |
4000 |
865,5 |
Балка поворотная |
865,5 |
|
ИВ2143 |
5,0 |
2000 |
789,4 |
Балка поворотная |
789,4 |
|
ИВ2144 |
4,5 |
2500 |
814,2 |
Балка поворотная |
814,2 |
|
ИВ2145 |
4,0 |
3200 |
818,8 |
Балка поворотная |
818,8 |
|
ЛГМ4х2000 |
4,0 |
2000 |
400,0 |
Балка поворотная |
400 |
|
ЛГМ4х2500 |
4,0 |
2500 |
450,0 |
Балка поворотная |
450 |
|
ИБ2216В |
4,0 |
2000 |
392,5 |
Трехвалковая |
981,25 |
|
ИВ2142 |
6,0 |
1600 |
710,0 |
Балка поворотная |
710 |
|
ИБ2220В |
10,0 |
2000 |
487,8 |
Трехвалковая |
1219,5 |
|
ИБ2222В |
16,0 |
2000 |
667,3 |
Трехвалковая |
1668,25 |
Вначале значение Кв принимается для машин с поворотной балкой равным 1. Машины трехвалковые, как видно из табл. 5.1, при одинаковых технических параметрах дешевле машин с поворотной балкой примерно на 60%, поэтому в первом приближении назначаем Кв для этих машин 0,4.
Статистической обработкой получили корреляционно-регрессионную модель, отражающую зависимость приведенной цены от влияющих параметров Хи х2: упр =F(Xl, х2). Гибридная модель зависимости реальной цены (стоимости) от всех рассматриваемых факторов, включая и фактор вида машины, будет иметь
Вид,:у=Квх/(х]9х2).
Расчет корреляционно-регрессионной модели выполнен средствами TV1S Excel. Для этого была использована функция ЛИ-НЕЙН. Так как она исчисляет параметры многофакторной линейной корреляционной модели, то исходную степенную функцию преобразуем в линейную форму, применяя прием логарифмирования.
Одновременно с построением корреляционно-регрессионной модели решается задача оптимизации значений коэффициента вида машины Кв' выполняемая по критерию минимума общего среднего квадратического отклонения для результатного показателя У, Т. е. Ау -> min.
Для проведения оптимизации коэффициентов вида машины была использована функция Поиск решения В системе MS Excel. Опишем порядок работы с данной функцией. В окно Поиск реШения Вводятся значения в такой последовательности. Указатель Целевая ячейка Заполняется номером ячейки, где содержится Су В матрице ЛИНЕЙН. Далее указывается условие минимизации этого критериального показателя. В указателе Изменяя ячейки Указываются номера ячеек, в которых находятся коэффициенты вида машины. В указателе Ограничения Вводится условие, согласно которому коэффициент вида равен 1 для машин с поворотной балкой.
После нажатия клавиши Выполнить Получаем оптимальное значение коэффициента вида для трехвалковых машин, равное 0,4.
Итоговая корреляционно-регрессионная модель для расчета полной стоимости замещения у листогибочных трехвалковых машин имеет вид:
У = 2,3934 Xxl0J65Xx2°'S*6XKB,
Где У — цена (полная стоимость замещения) листогибочной машины, тыс.
Руб.;
Х1 — наибольшая толщина сгибаемого листа, мм; Х2 — Наибольшая ширина сгибаемого листа, мм; Кв — коэффициент вида машины: с поворотной балкой — 1, трехвалковая
Машина — 0,4.
Для создания комплекса математических факторно-стоимостных моделей был проанализирован рынок технологического металлообрабатывающего оборудования в Москве по состоянию на начало 2003 г. Источником информации послужили прайс-листы ведущих дилерских компаний «Дюкон», «АСВ», «ДВТ», «СТ Маркет» и «Ками».
В предлагаемой к продаже номенклатуре машин и оборудования были выделены 11 группировок, число моделей в каждой должно быть не менее 10. Эти группировки использовались для построения факторно-стоимостных моделей. Остальные модели машин встречаются на рынке либо единично, либо в весьма малых (до 4) группах. Поэтому недостаточная насыщенность российского рынка оборудованием не позволяет пока полностью охватить его математическим моделированием. Тем не менее разработанные математические модели для 11 групп металлообрабатывающего оборудования охватывают почти 80% исследованного сегмента рынка в Москве (приложение 2).
Разрабатываемые по описанной выше методике факторно-стоимостные математические модели позволяют оценивать полную стоимость замещения (восстановительную стоимость - при переоценке), так как исходной базой для их построения являются цены предложения на новые единицы оборудования в состоянии их готовности к продаже и в том месте, где собрана ценовая информация. В течение примерно 3 лет результаты, полученные с помощью данных моделей, можно обычным образом корректировать соответствующими индексами-дефляторами, в дальнейшем требуется повторная процедура разработки моделей, чтобы учесть происходящие изменения рыночной конъюнктуры.
Для применения факторно-стоимостных математических моделей при массовой оценке необходимо разработать соответствующее программное средство. В качестве примера покажем использование ресурсов MS Excel для решения этой задачи. Этапы расчетного алгоритма представлены на рис. 5.1.
Этап 1. Фильтрация списка оборудования, подлежащего оценке. Исходный список машин и оборудования нуждается в предварительной фильтрации, так как не все единицы оборудования в списке могут быть оценены с помощью моделей массовой оценки. Состав разработанных математических моделей не может покрыть все встречающиеся при оценке объекты.
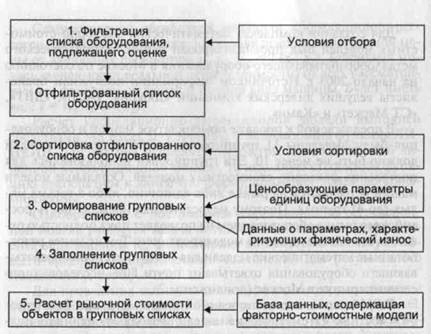
Рис. 5.1. Принципиальная схема функционирования программной системы
С течением времени по мере разработки все новых моделей будет расширяться и состав подлежащих компьютерной массовой оценке объектов, в силу чего необходимо провести фильтрацию исходного списка, чтобы выделить из него те объекты, для оценки которых имеются в настоящее время факторно-стоимостные модели.
В исходном списке для каждого объекта указаны следующие данные:
• наименование, модель, характеристики;
• инвентарный номер;
• код места положения;
• код ОКОФ;
• месяц - год ввода (изготовления).
При работе с MS Excel формируется рабочая книга «Массовая оценка». Первый лист этой книги называется «Исходный список». Пример работы со списком (в сокращенном виде) для объектов предприятия АО «Прожекторный завод» приведен в приложении 3.
Признаком применения той или иной математической модели для конкретной единицы оборудования является ее код ОКОФ, по которому осуществляется фильтрация исходного списка.
Этот процесс происходит в такой последовательности:
1) в начале листа «Исходный список» скопирован список заголовков фильтруемых столбцов, под ним оставлены несколько строк для внесения в них условий отбора. В нашем случае условием отбора записей будет список кодов ОКОФ, на которые имеются разработанные факторно-стоимостные модели. По первоначальному состоянию в столбец «Код ОКОФ» были внесены 11 кодов ОКОФ: 142922105, 142922111, 142922121, 142922123, 142922129, 142922150, 142922165, 142922191, 142922202, 142922248, 142922251;
2) выделяем область исходных данных, т. е. весь исходный список вместе с названиями столбцов;
3) в меню Данные Выбираем пункт Фильтр, А затем команду Расширенный фильтр. Появляется диалоговое окно Расширенный Фильтр;
4) в диалоговом поле Расширенный фильтр Отмечаем в строке «Исходный диапазон» интервал ячеек, охватывающий исходный список данных; в строке Диапазон условий — интервал ячеек, охватывающий положение начальной вспомогательной таблицы со списком указанных выше кодов ОКОФ;
5) переключатель Обработка Ставим в положение Скопировать Результат в другое место. В Строке Поместить результат в диапазон Указываем интервал ячеек, где разместится на данном листе отфильтрованный список;
6) нажимаем кнопку ОК и получаем новый список объектов, для оценки которых применимы разработанные факторно-стоимостные модели.
Полученный список нуждается в дальнейшей сортировке с тем, чтобы сгруппировать объекты (записи) по признакам: код ОКОФ, код места положения и месяц — год ввода (изготовления).
Этап 2. Сортировка отфильтрованного списка. Последовательность сортировки такова:
1) выделяем отфильтрованный список без названия столбцов (полей);
2) В Меню Данные Выбираем команду Сортировка. Появляется диалоговое окно Сортировка диапазона;
3) в строке Сортировать по Выбираем Столбец, Который соответствует полю Код ОКОФ. Таким образом, первым признаком сортировки является Код ОКОФ;
4) в строке Затем по Указываем Столбец Н, Который соответствует полю Код места положения. Таким образом, вторым признаком сортировки является код местоположения;
5) в строке В последнюю очередь, по Указываем Столбец J, Соответствующий полю Месяц - год ввода (изготовления). Таким образом, третьим признаком сортировки служит месяц — год ввода (изготовления);
6) в перечисленных выше трех строках переключатели должны быть в положении По возрастанию;
7) переключатель Идентифицировать поля по Должен соответствовать Обозначениям столбцов листа;
8) Щелкаем кнопку ОК и получаем отсортированный список объектов для оценки.
Для удобства работы со списком вставляем пустые строки между записями, относящимися к одной группе ОКОФ.
Этап 3. Формирование групповых списков. В Программе для каждого кода ОКОФ подготовлена форма группового списка. Всего таких форм 11.
Первые три столбца у всех форм имеют одинаковые заголовки (поля), которые повторяют первые три поля исходного списка.
Следующие четыре столбца имеют заголовки, обозначающие названия ценообразующих параметров, входящих в соответствующую факторно-стоимостную модель.
Следующие два столбца имеют заголовки: «Физическое состояние в баллах» и «Номер последнего капитального ремонта». Эти показатели используются для определения коэффициента физического износа.
Следующие два столбца имеют заголовки: «Коэффициент физического износа» и «Рыночная стоимость».
Этап 4. Заполнение групповых списков. Первые три столбца в групповых списках заполняются путем копирования данных из соответствующих блоков отсортированного списка объектов.
В остальные шесть столбцов вводят сведения О Параметрах объектов.
Этап 5. Расчет рыночной стоимости объектов в групповых Списках. В последнем столбце компьютер рассчитывает искомую рыночную стоимость каждого объекта.
Метод построения факторно-стоимостных моделей обладает тем преимуществом, что позволяет учесть полезностью свойства оцениваемых объектов и получить благодаря этому полную стоимость замещения. Особенно выгодно использование этого метода при оценке старого импортного или отечественного, но уже не выпускаемого оборудования, для которого известны технические характеристики, но невозможно сегодня подобрать прямого аналога. Хотя сбор сведений о ценообразующих параметрах оцениваемых объектов несколько затягивает оценочную процедуру.
Не исключено, что в перспективе будут создаваться базы данных не только из сведений о многочисленных единичных объектах, а и из факторно-стоимостных моделей по однородным группам, что расширит применимость этого метода.

 Опубликовано в
Опубликовано в